脑电信号的分形截距特征分析及在癫痫检测中的应用

王 玉 周卫东 李淑芳 袁 琦 耿淑娟

(山东大学信息科学与工程学院，济南 250100)

引言

癫痫是一种脑部神经元过度放电、引起突然反复和短暂的中枢神经系统功能失常的慢性脑部疾病，具有突然性、暂时性、反复性三大特点。脑电图(EEG)是脑神经细胞电活动在大脑皮层或头皮表面的总体反映，在癫痫的诊断和治疗中是一种非常重要的工具［1－2］。在癫痫发作间歇期(interictal)、发作前期(preictal)和发作期(ictal)，其脑电活动也随之发生变化。临床上癫痫发作诊断所使用的方法为目测法，即通过观察脑电信号中的癫痫特征波来诊断癫痫发作。通常，用于癫痫发作诊断的脑电信号持续很长时间，有时甚至长达几天，分析如此长的脑电信号耗费专家大量的精力。因此，近年来人们利用癫痫发作前后脑电信号某些特征量的差异来检测和预测癫痫发作。

大脑在许多状态下的脑电时间序列都具有明显的非线性特征，脑电的非线性特性分析逐渐成为一个研究热点［3－5］，如李雅普诺夫指数、关联维数、近似熵、非线性预测等被用于脑电分析［6－9］。研究发现:常规脑电的波形、波幅、频率等指标提供的信息，还不能充分描述癫痫发作过程中的脑电活动;随着癫痫的发作，脑电的非线性动力学特征会发生明显的变化，脑电活动的相关维数、分形维数、李亚普诺夫指数、自由度等非线性指标会逐渐降低［10－11］。因此，通过非线性动力学研究癫痫，是一种有效的手段。

分形几何学认为，客观事物的局部与整体在形态、功能、信息、时间、空间等方面具有统计意义上的相似性。为了描述不规则结构的分形特征，针对不同的分形结构，常常提取它们的分形维数、分形截距、缺项等特征［12］。其中，分形维数是对事物的复杂程度、粗糙程度、不规则程度、对空间的有效占有程度等性质的一种测度，分形截距则反映不规则物体表面变化的快慢。Peleg等提出使用覆盖技术计算图像表面分形维数的方法，即毯子维［13］。毯子覆盖技术与其他分形理论相比，能在不同分辨能力下获得物体的变化特性。现有用分形方法分析脑电信号的研究，都是利用相关维数、分形维数等作为特征［14－15］。本研究对癫痫脑电信号进行了基于毯子维的分形截距特征分析，并将其应用于癫痫脑电信号的检测。此外，针对癫痫发作前后脑电信号的分形截距和毯子维特征进行对比研究。

1 脑电特征分析

1.1 毯子维和分形截距

将图像g(i，j)看作是三维空间中的曲面，(i，j)为二维平面的横纵坐标，图像的灰度值为Z轴坐标。在距离曲面两侧δ内的所有点构成厚度为2δ的“毯子”，灰度图像的毯子维可以由此三维曲面计算得到［16］。首先，假定第0层毯子的上下表面为原始图像，即

然后使用式(2)和式(3)获得各层毯子的上下表面，有

式中，δ表示毯子的层数，δ=1，2，3…。设各层毯子的厚度(即上下表面的距离)为2δ，毯子的体积和表面积可分别由式(4)和式(5)获得，有

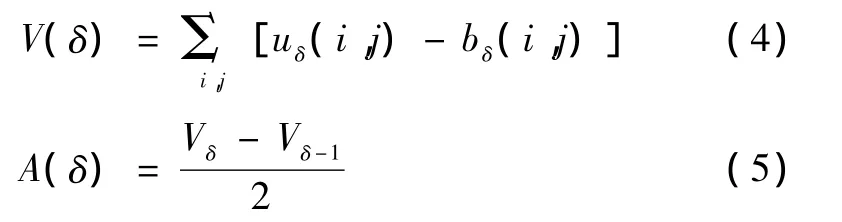
基于Minkowski维数和覆盖技术，有

两边取自然对数，则

式中，β为常数，C1=2－D为直线的斜率，C0=lnβ为直线的截距(分形截距)。

斜率和截距各代表不同的物理意义:毯子维数D(D=2－C1)反映了图像表面的不规则程度，而分形截距能够反映图像灰度值变化的快慢程度。

1.2 脑电分形特征提取

为了对一维脑电时间序列提取毯子维和分形截距特征，将上下所有与脑电信号距离小于δ的点视为一个宽为2δ的条状带，条状带的面积可以用信号长度与条状带的宽度乘积得到。本研究用毯子法，计算时间序列毯子维和分形截距特征。

步骤1:设有L个数据点的一维脑电信号g(i)，(i≤L)，将此脑电信号均匀地分成M个子段，每段有 N 点，即 g(i)= ［g1(i)，g2(i)，…，gM(i)］。

步骤2:令第0层覆盖线u0(i)=b0(i)=gj(i)，j∈［1，M］，计算上下各层覆盖线的长度，有

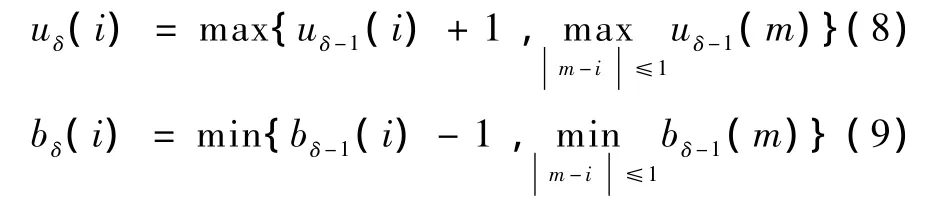
根据式(8)和式(9)算出上下覆盖线，得

步骤 3:对于不同的 δ，如 δ1、δ2，得到 A(δ1)、A(δ2)，根据式(7)，有

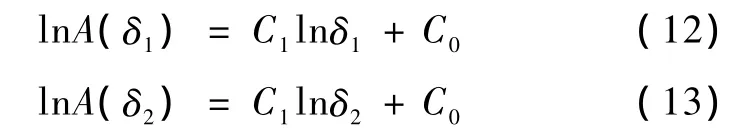
得到毯子维及分形截距，有

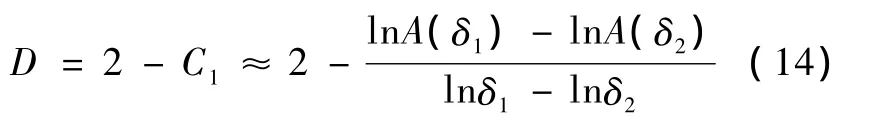
步骤4:对M段脑电数据，分别求分形截距特征和毯子维特征，最终得到对应脑电数据g的分形截距特征向量 C= ［C01，C02，…，C0M］和毯子维特征向量 D= ［D1，D2，…，DM］。

2 实验研究

2.1 实验数据

实验数据分别来自德国波恩癫痫研究室临床采集的脑电数据库和山东大学齐鲁医院的临床脑电。波恩癫痫研究室的脑电数据已被广泛用于癫痫病的诊断和分析研究，其中包括5类脑电数据，每一类有100段时长为23.6 s的脑电信号，采样频率为173.6 Hz，脑电数据中的手动或眼动等干扰已被去除［17－18］。选取其中间歇期脑电(D组)和发作时的癫痫脑电(E组)各100段，每段4 097点。在实验中，将每段数据分为相等的4小段，每小段数据1 024个点，共得到间歇期脑电和癫痫脑电各400小段数据。

山东大学齐鲁医院的脑电数据来自临床确诊的癫痫病例6名，采样频率为128 Hz。选取间歇期脑电和发作期癫痫脑电各512段，每段1 024点。

2.2 脑电分形截距与毯子维分析

分别选取波恩和儿童医院数据中间歇期脑电和癫痫脑电各10段，每段1 024点，按照L=1 024，M=1，N=1 024的情况利用毯子法提取分形截距特征，图1给出了间歇期脑电和癫痫脑电按式(7)得到的直线(lnA(δ)=C1lnδ+C0)的分布。

从图1中可以发现，间歇期脑电与癫痫脑电的斜率(对应毯子维特征)变化不大，但是上下位置有明显不同，即两种脑电数据的分形截距有明显差异。为进一步分析癫痫脑电和间歇期脑电信号的毯子维与分形截距特征的差异，图2给出了波恩数据库中间歇期脑电和癫痫脑电的毯子维及分形截距对比。两种特征的均值及标准差如图3所示。

从图2可以看出，波恩脑电数据中间歇期脑电和癫痫脑电的分形截距特征能很好地分开(如图2(b))，而毯子维特征有明显的交叠(如图2(a))。图3表明，波恩脑电数据中间歇期脑电和癫痫脑电的毯子维均值差异很小(癫痫脑电均值为2.66、标准差为0.22;间歇期脑电均值为 2.45、标准差为0.10)，而分形截距均值差异较大(癫痫脑电均值为11.55，标准差为0.65;间歇期脑电均值为9.47，标准差为0.51)。

图2 波恩脑电数据毯子维及分形截距对比(·代表癫痫脑电，+代表间歇期脑电)。(a)毯子维特征;(b)分形截距特征Fig.2 Comparison of blanket dimension and fractal intercept features for EEG data of Bonn (“·”representsictalEEG，“ +” representsinterictal EEG).(a)Blanket dimension feature;(b)Fractal intercept feature

图4给出了齐鲁医院数据库中间歇期脑电和癫痫脑电的毯子维特征及分形截距特征的对比，其中·代表癫痫脑电，+代表间歇期脑电。对应图4的毯子维和分形截距特征均值及标准差的对比如图5所示。由图4发现，在齐鲁医院脑电数据中，间歇期脑电和癫痫脑电的分形截距特征同样能够很好地分开，而毯子维特征有多处交叠。同样，图5显示，齐鲁医院脑电数据中间歇期脑电和癫痫脑电的毯子维特征均值差异很小(癫痫脑电均值为2.54，标准差为0.21;间歇期脑电均值为 2.45，标准差为0.14)，而分形截距均值差异较大(癫痫脑电均值为10.3，标准差为0.51;间歇期脑电均值为8.94，标准差为0.21)。

图3 波恩脑电数据毯子维及分形截距均值和标准差对比。(a)毯子维特征;(b)分形截距特征Fig.3 Comparison of the mean and standard deviation between blanket dimension and fractal intercept features for EEG data of Bonn.(a)blanket dimension feature; (b)fractal intercept feature

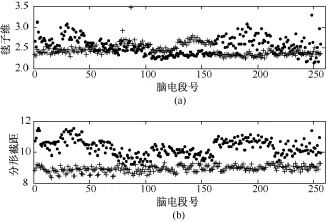
图4 齐鲁医院脑电数据毯子维及分形截距对比(·代表癫痫脑电，+代表间歇期脑电)。(a)毯子维特征;(b)分形截距特征Fig.4 Comparison of blanket dimension and fractal intercept features for EEG data of Qilu Hospital(“·”represents ictal EEG，“+”represents interictal EEG).(a)blanket dimension feature;(b)fractal intercept feature

2.3 癫痫脑电的检测

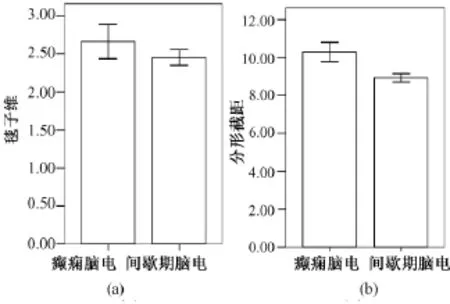
图5 齐鲁医院脑电数据毯子维及分形截距均值和标准差对比。(a)毯子维特征;(b)分形截距特征Fig.5 Comparison of the mean and standard deviation between blanket dimension and fractal intercept features for EEG data of Qilu Hospital.(a)blanketdimension feature;(b)fractal intercept feature

支持向量机(SVM)是根据统计学习理论提出的一种新的机器学习方法，具有很好的推广能力［19］。SVM的基本思想是对于线性不可分样本，经非线性变换将其映射到另一个高维空间中，在变换后的空间中寻找一个最优分界面(超平面)，使之线性可分。为实现癫痫脑电检测，按文中1.2的步骤，将长度L为1 024点的脑电数据段，分割成等长M个子段，每个子段长度为N，得到M个分形截距特征，组成该段脑电数据的分形截距特征向量，然后送入支持向量机(SVM)分类器进行训练和分类测试，其中训练数据和测试数据各占一半。表1和表2给出了波恩和齐鲁医院癫痫脑电自动检测的结果，其中准确率为癫痫脑电和间歇期脑电中被正确检出的比率。

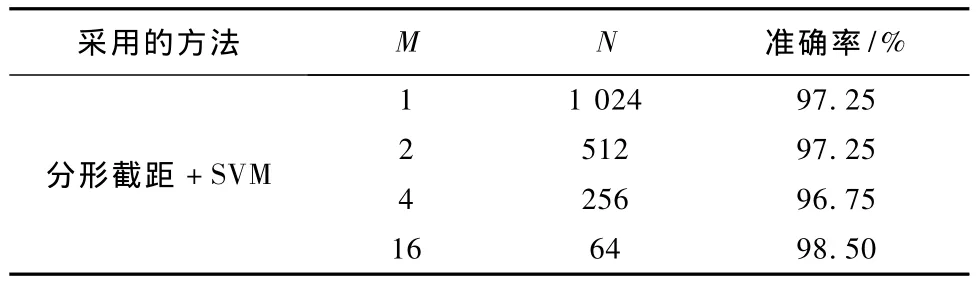
表1 德国波恩脑电数据检测结果Tab.1 Detection results of EEG data in Bonn

表2 齐鲁医院脑电数据检测结果Tab.2 Detection results of EEG data in Qilu Hospital

从表1和表2中观察到，采用SVM分类器对癫痫脑电和间歇期脑电的分形截距特征进行分类，可以取得很好的检测效果;对脑电数据进行不同长度分段，正确识别准确率具有较好的稳定性，说明了分形截距特征对于数据长度的稳定性。

3 讨论和结论

脑电在癫痫发作期较间歇期幅度变化大，波动剧烈。基于毯子维的分形截距特征可以描述脑电数据在不同分辨率下变化的剧烈程度，实验中癫痫脑电的分形截距特征明显高于间歇期脑电信号，两者具有明显差异，而脑电信号的毯子维在发作前后变化规律则不明显，因此可将分形截距作为癫痫脑电和间歇期脑电的分类依据。分形截距特征可为癫痫脑电的特性分析、自动检测和癫痫发作预测提供有意义的参考，也为研究癫痫脑电的非线性动力学特性提供了一种有效途径。

由于目前治疗方法的局限，一些顽固性癫痫患者得不到有效治疗。若能在癫痫发作前预测到癫痫即将发作，即使是较短的时间，也可使患者或医生能够及时采取必要的预防保护措施，从而降低癫痫发作造成的损害。目前仅将分形截距特征用于癫痫脑电的检测，下一步拟针对癫痫发作的非线性预测做进一步研究。

本研究将二维的毯子维和分形截距算法进行改进，使其适合一维信号的非线性特征提取;对癫痫脑电信号进行了毯子维和分形截距特征分析，并将分形截距特征应用于癫痫脑电信号的检测。研究发现，癫痫脑电信号的分形截距特征明显大于间歇期脑电的分形截距特征，而脑电信号的毯子维在发作前后变化规律不明显。相对毯子维特征而言，分形截距特征更能明显地区分癫痫脑电和间歇期脑电，且对数据长度有较好的稳定性。

癫痫已成为脑电非线性分析研究的热点和前沿。对脑电进行非线性分析，有助于理解癫痫发生过程中脑电的变化，并可进一步用于癫痫检测和预测癫痫的发作。基于毯子维的分形截距特征能够很好地描述脑电数据在不同分辨率下的变化特性，可有效地区分癫痫脑电与间歇期脑电，具有较强的癫痫脑电检测性能。

(致谢 论文工作得到了山东大学齐鲁医院王纪文主任医师和贾桂娟技师的帮助，在此表示感谢。)

［1］李勇，高小榕，杨福生，等.高分辨脑电图的理论研究［J］.中国生物医学工程学报，2005，24(1):59－65.

［2］黄远桂，吴声伶.临床脑电图学［M］.西安:陕西科学技术出版社，1984:162－195.

［3］KannathalN， Rajendra AcharyaU， Lim C M， etal.Charateriaztion of EEG:a comparative study［J］.Computer Methods and Programs in Biomedicine，2005，80(1):17－23.

［4］范金锋，邵晨曦，王剑，等.醉酒者脑电和正常脑电非线性特征的比较评估［J］.中国生物医学工程学报，2008，27(1):18－28.

［5］蔡冬梅，周卫东，刘凯，等.基于Hurst指数和SVM的脑电癫痫检测方法［J］.中国生物医学工程学报，2010，29(6):836－840.

［6］任志军，田心.脑电高阶Lyapunov指数的估计及其仿真计算［J］.中国生物医学工程学报，2005，24(6):676 －680.

［7］李春胜，王宏，赵海滨，等.脑电混沌维数复杂度连续检测方法的研究［J］.中国生物医学工程学报，2009，28(6):846－850.

［8］Srinivasan V，Sriraam N.Approximate entropy-based epileptic EEG detection using artificial neural networks［J］. IEEE Transaction on Information Technology in Biomedicine Engineering.2007，11(3):288－295.

［9］孟庆芳，周卫东，陈月辉，等.基于非线性预测效果的癫痫脑电信号的特征提取方法［J］.物理学报，2010，59(1):123－129.

［10］Silva C，Pimentel IR，Andrade A，et al.Correlation dimension maps of EEG from epileptic absences［J］.Brain Topogr，1999，11(3):201－209.

［11］Widman G，Lehnertz K，Urbach H，et al.Spatial distribution of neuronal complexity loss in neocortical lesional epilepsies［J］.Epilepsia:Journal of the International League against Epilepsy，2000，41(7):811－817.

［12］赵莹.基于分形几何学的图像信息表示及其应用研究［D］.合肥:合肥工业大学，2009.

［13］Shmuel P，Joseph N，Ralph H，et al.Multiple Resolution texture Analysis and Classification［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1984，6(4):518 －523.

［14］赵龙莲，梁作清，伍文清，等.生物反馈训练后癫痫患者脑电相关维数变化的分析［J］.中国生物医学工程学报，2010，29(1):71－76.

［15］杨浩，方良，何为.脑电信号分数维值的分析研究［J］.生物医学工程学杂志，2004，24(1):81 －84.

［16］Chaudhuri B B，Nirupam S.Texture segmentation using fractal dimensions［J］.IEEE Transactions on Pattern Analysis and Machine Intelligent，1995，17(1):72 －77.

［17］Gautama T， MandicDP， VanHulleMM. Indicationsof nonlinear structures in brain electrical activity［J］，Physical Review E，2003 67:046204.

［18］Andrzejak RG，Lehnertz K，Mormann F，et al.Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity:Dependence on recording region and brain state［J］.Physical Review，2001，64(6):061907.

［19］边肇祺，张学工.模式识别［M］.(第二版).北京:清华大学出版社，2000:296－303.