一种新的T波交替量化评估联合算法

万相奎 谢富兰 王美林

1(广东工业大学信息工程学院，广州 510006)

2(广州医学院荔湾医院心内科，广州 510170)

引言

心脏性猝死(sudden cardiac death，SCD)是心血管疾病死亡的主要原因。据美国心脏病协会统计，美国每年大约有40万例心脏性猝死［1］。我国有文献称年发病率达0.18%，全国每年180万人发生SCD，经临床证实为 0.036% ～0.128%［2］。对于有SCD潜在危险的病人，目前一般采用电生理方法(electrophysiology，EP)来处理。但是，由于 EP风险大，费用高，耗时长，因而限制了它的应用。其他的无创伤性预测方法，如心室晚电位(ventricular late potential，VLP)、QT 离散度(QTa)等，从目前应用的实际情况看，还缺乏足够的可信度。

T波交替(T wave alternans，TWA)是指T波每隔一个激动就发生振幅、宽度或形态的重复现象，它反映了心室复极化过程的时间和空间的不均匀性传播。大量的临床实验和研究文献表明［3－5］:TWA与室性心律失常有密切的关系，是预测发生恶性室性心律失常和SCD的独立且具有统计学意义的指标。当前，TWA的评估算法研究已引起广泛注意，有望发展成为一种优越的、无创评定发生心脏猝死危险性的技术。

目前，TWA的评估算法主要包括频域法和时域法两大类。频域法中Adam等最早提出了能量谱法(energy spectral method，ESM)［6］，其后又有很多学者在此基础之上进行改进和发展，具有代表性的是Smith 等提出的谱分析法 (spectral method，SM)［8］、Nearing等提出的复数解调法 (complex demodulation，CD)［9］，以及 Laguna 等将 KL 变换和谱分析法结合起来形成的 KLSM［10］。总的来说，频域法对输入数据的要求较低，抗噪声和呼吸调制等干扰的能力较强，但同时存在无法有效检测数据中的非稳态现象、不具备时间分辨率的缺点，对TWA现象的非平稳特征无法做出有效的识别。另外，这些方法也不能在运动试验或动态心电图检查时进行分析，因而影响了频域法TWA的推广使用。

在时域方面，典型的有 Nearing提出的修正移动 平 均 法 (modified moving averagemethod，MMA)［11］，以 及 Burattini 等 提 出 的 相 关 分 析 法(correlation method，CM)［12］。时域法能够较好地跟踪非稳态的TWA现象，其基本思想是从时间序列的角度来分析TWA。时域分析法可在动态心电图或平板运动试验中检测TWA，具有很好的时间分辨率，也无需固定心率和时间，受检者可自由活动，可动态捕捉短暂而剧烈的心律失常。但时域法对信号的质量要求较高，目前尚无统一的采样方案和诊断标准。

除了上述两大类算法外，还有诸如拉普拉斯似然比法、沃尔什函数法、庞加莱映射法等基于统计方法和非线性处理的方法［7］，这些方法仅出现于相关研究文献中，没有看到其实际应用情况的报道。

小波变换作为一种时频分析技术，可以提供信号时间域与频率域的联合分布信息，清楚地描述信号频率随时间变化的关系。本研究基于ECG信号连续小波变换，提取T波序列的时频特征信息;从频率域角度计算其能量谱，运用非参数检验中的Wilcoxon秩和检验法定性检测 TWA;在此基础上，运用相关分析方法，从时域角度定量评估TWA，为心律失常的治疗和心脏猝死事件的预测分析提供更为可靠和丰富的临床信息。

1 TWA检测与分析算法

1.1 连续小波变换分析

连续小波变换具有多分辨率分析的特点，在时频两域都具有表征信号局部特征的能力，是一种窗口大小固定不变但其形状可改变、时间窗和频率窗都可以改变的时频局部化分析方法。连续小波变换不同于传统的短时傅里叶变换之处，在于其具有更好的时频窗口特性。对不同的频率在时域上的取样步长是调节性的，即在低频时小波变换的时间分辨率较差，而频率分辨率较高;高频时小波变换的时间分辨率较高，而频率分辨率较低。所以，连续小波变换既能提取信号的局部特征信息，也能提取其全局特征信息。

若存在信号f(t)∈L2(R)，则f(t)的连续小波可变换为

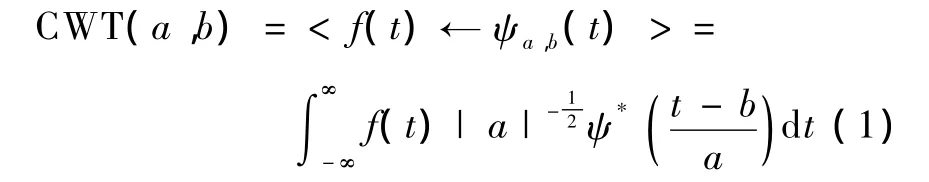
式中，ψ(t)∈ L2(R)为母小波函数，上标*表示共轭。

ψ(t)作为小波函数的条件是其傅里叶变换ψ(ω)必须满足以下容许性条件，即

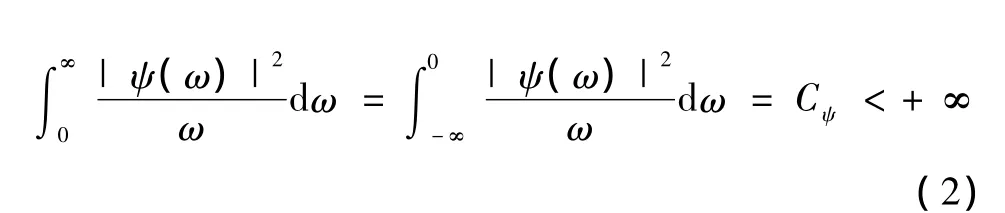
这一条件意味着小波在时域和频域内均是紧支撑的。

a，b分别是尺度(平移)和伸缩因子参数(a，b∈R且a＞0)，基本小波ψ(t)的伸缩间期取决于尺度因子a。

信号f(t)在尺度因子a和伸缩因子b处的能量谱分布以二维的小波能量密度函数可表示为

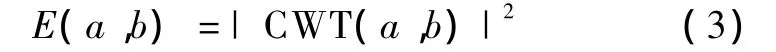
1.2 ECG信号预处理

ECG的噪声主要包括工频干扰、基线漂移、肌电干扰及电极移动产生的噪声。本研究对以50 Hz及其各次谐波构成的工频干扰，采用文献［13］提出的自适应notch滤波器来完成;基线漂移和电极移动产生的干扰通常小于5 Hz，采用文献［14］提出的三次样条差值法来纠正;肌电干扰采用文献［15］去噪算法来降低噪声影响。

对降噪处理后的ECG数据，采用小波变换模极大值对的方法来确定所有R波的波峰。以RR间期方差是否小于RR间期均值的10%为判据来定RR间期是否平稳［16］，这样既防止过大的心动周期波动所造成的心电波形的变化，剔除异常心拍，又保证TWA分析的心电数据中必要的生理性和病理性的心率波动。在RR间期检测结果平稳的基础上，根据R波峰的定位结果，确定 T波窗口，最后进行TWA检测。为避免由于特征点定位误差造成的结果偏差累计，采用独立于T波起点和终点检测的加窗法，根据R波峰值位置以及 T波窗口的长度，描述T波窗口的大小和位置。

1.3 TWA定性检测与量化分析

Wilcoxon秩和检验是基于样本数据秩和的一种统计分析方法，广泛应用于两组独立样本未知分布的情况下，以判定它们是否来自相同分布的总体。若一段ECG信号含有TWA，即T波存在幅值的交替变化，则各T波所对应的能量谱也应呈现对应的变化。因此，可根据式(3)提取各心电节拍的T波能量谱，构成奇偶两组T波序列，即两组未知分布的独立样本。显然，这两组样本符合Wilcoxon秩和检验要求，因此可对它们统一编秩，再运用Wilcoxon秩和检验进行测试。相对TWA时域检测法而言，TWA谱分析法从T波交替的频率角度来检测，对信号质量相对要求较低，在信噪比相对较弱的情况下仍可以可靠和准确地检测 TWA［17－18］。对 T波序列的能量谱运用Wilcoxon秩和检验来定性判别，其基本原理仍是建立在频谱分析基础上，因此抗干扰性强。

［19］，若奇偶T波样本序列属于同一样本的概率低于0.05(P＜0.05)，则表示奇、偶 T波样本不属于同一总体分布，即被分析的T波序列中被定性检测出含有TWA现象;否则，则表示分析的奇、偶T波样本属于同一总体分布，即该段信号中没有TWA出现。这一定性检测算法采取以下具体流程。

步骤1:数据预处理后，对ECG信号进行连续小波变换，以小波变换的模极大值对方法检测出R波峰，进而计算出平均RR间期;根据连续小波变换的结果，获取ECG信号的时频信息。

步骤 2:以各 R波峰为基准，Tsk=40+作为 T波起点 ，其后400 ms处为 T波终点，定义T波分析窗。

步骤3:T波能量主要分布在0.5～10 Hz范围内。因此，可根据以上划定的时频区域，在 ECG中提取每个心电节拍的T波时频信息，并获取其在划定时间内(400 ms)的能量谱Ei，最终获得T波能量谱序列En。这一过程如图1所示，(a)为500 Hz采样频率采集的单个心拍时域信号，(b)为该心拍的时频分布，(c)为步骤2及其所提取心拍的 T波时频能量谱。

图1 T波时频特征提取。(a)一个心电节拍;(b)该信号的小波时频;(c)T波能量谱Fig.1 Time-frequency feature extraction of T wave.(a)a rhythm;(b)wavelet time-frequency figure of the rhythm(c)total energy of the T wave

步骤4:对T波能量谱序列En按奇、偶划分为两组，E2i+1、E2i构成奇、偶序列样本，分别对应奇数序列和偶数序列的T波。应用Wilcoxon秩和检验方法，在对其进行统一编秩后，计算奇序列E2i+1和偶序列E2i样本来自同一分布的概率p。

步骤5:判断是否存在TWA，若P＜0.05，可认为奇序列E2i+1和偶序列E2i样本不是来自同一分布的样本，即存在 TWA;反之，若 P＞0.05，则认为被分析的ECG中没有TWA出现。

定性检测出存在TWA的ECG信号，再基于相关技术［12］量化分析T波间的相关程度，从而实现对TWA交替的时域量化分析。

1)提取出T波序列，计算出平均 T波Tm，有

式中，N为被分析的ECG信号中包含的T波总数。

2)计算T波交替相关指数和交替个数。定义交替相关指数ACI为当前心拍的 T波 Ti与平均 T波Tm的互相关值与Tm自相关值的比值，有

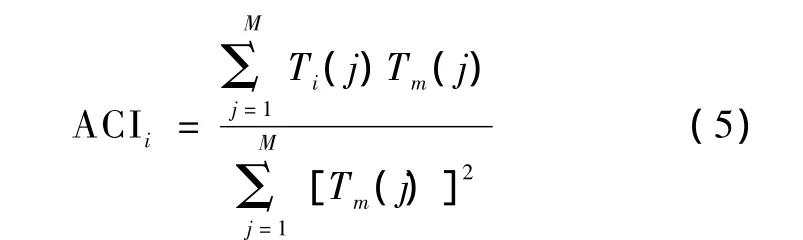
式中，M为每个心拍的T波采样点数。

ACIi量化反映了单个心拍的T波与平均T波的交替水平。如果ACIi的大小不为1，且存在连续7个或以上的ACIi值围绕1严格有序地上下波动，则标记TWA在第一个波动的ACIi所对应的T波处开始;反之，当出现ACIi不再围绕1上下波动，则标记TWA在该T波处结束。

3)计算单个TWA交替幅值。在获得单个T波交替相关指数ACIi的基础上，定义单个心拍的T波交替程度表征量——交替幅值ACMi，有

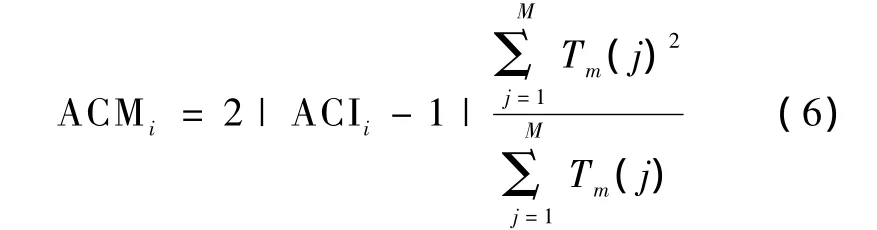
4)计算TWA平均交替幅值。整个被分析的ECG段的TWA平均交替幅值可定义为

2 算法实验

2.1 仿真实验

微伏级TWA人眼无法识别，因此用特定算法来TWA时，其正确性和鲁棒性通常是无法知晓的。为了评估本算法对TWA检测的有效性，本研究首先对模拟信号进行了仿真实验。

模拟信号S由合成ECG信号、噪声信号和拟合交替段组成，其模型定义为

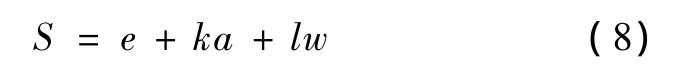
式中，e为单个心拍重复连接而组成的合成ECG;a为拟合的交替波形，k为交替水平;w为噪声，l为噪声强度因子，通过设置 l可控制模拟信号的信噪比。

心电信号的噪声w主要包括基线漂移(baseline wandering，bw)、肌电噪声(muscular activity，ma)、电极移动噪声(electrode motion，em)和白噪声(white noise，wn)，这一模拟信号实现方案如图2所示。

图2 含TWA的仿真ECG信号合成方案Fig.2 Synthetical scheme of simulated ECG with TWA

模拟信号S的具体获取过程如下:

1)在静息状况下，用专用高信噪比采集设备、以500 Hz采样频率，从健康受试者体表采集 ECG信号。从中选择一个“干净”的心电节拍，时长为1 s。对该节拍重复1 000次后，构成一个1 000 s时长的合成ECG信号e。这使得T波都是一致的，确保合成的ECG中不会出现TWA。以同样的方法，从另外4位健康受试者中获得4段合成的ECG信号。这样获取5段合成ECG信号。

2)分别以高斯函数及其一阶导数对应的波形来模拟交替波形。每种波形对应5种不同交替水平的交替因子，分别设定为 10、20、50、100、200 μV，构造出10种不同的TWA段。在以上合成的5段ECG信号中，每隔一个心拍对T波进行叠加，最终获得50段含TWA段的模拟ECG信号S。

3)从美国PhysioBank数据库的 MIT-BIH心电噪声测试数据库中，分别获取bw、ma和em信号，并用Matlab生成高斯白噪声。将以上噪声叠加后，获得噪声信号w，通过调整噪声强度因子l，分别与前面获取的50段合成ECG信号混合，构造出信噪比分别为 20、25、30、35、40 的 250 段含噪模拟信号(S=e+ka+lw)。

定义算法的灵敏性(Se)为

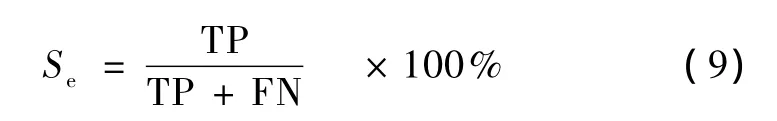
式中，TP为真阳性数目，即正确检测出的真实存在TWA的ECG数目;FN为假阴性数目，即漏检的含TWA的ECG数目。

运用文中第2节提出的算法，对以上模拟的时长为1 000 s的各段ECG信号进行分析。

250段模拟ECG信号定性检测，结果显示其中的228例 ECG中出现 TWA现象(P＜0.05)，TWA检测的平均灵敏性Se达91.2%。不同信噪比和不同交替水平下检测的具体数据如表1所示。

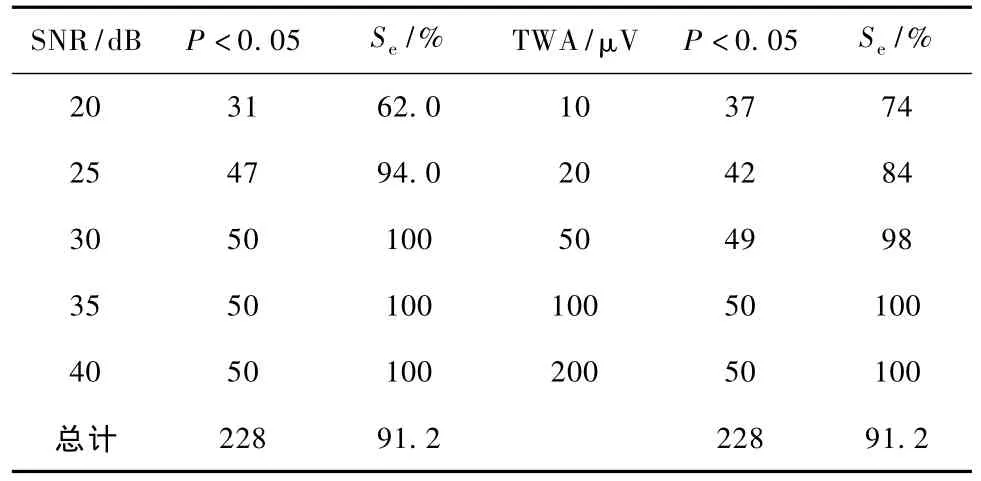
表1 定性检测实验数据Tab.1 Qualitative detection experiment data

由表1可见，在信噪比高于30时，可以100%准确地检测出TWA。在T波交替因子幅值高于100 μV时，可以100%正确地检测出 TWA;在 TWA为50 μV时，检测灵敏性达98%。

如果合成的ECG均不加入模拟的TWA交替因子，而是直接与混合噪声构建不同的信噪比(SNR=20，25，30，35，40)，则此时的检测正确率达 92% 。

对检测出含TWA的ECG信号，在不同TWA级(10/20/50/100/200 μV)、不同信噪比下各取 1段信号，对这25段ECG信号运用相关分析技术进行T波交替水平量化分析。不同交替水平下的测量结果如表2所示，其中平均为同一TWA级别下不同信噪比(SNR=20，25，30，35，40)计算获得的的平均值。

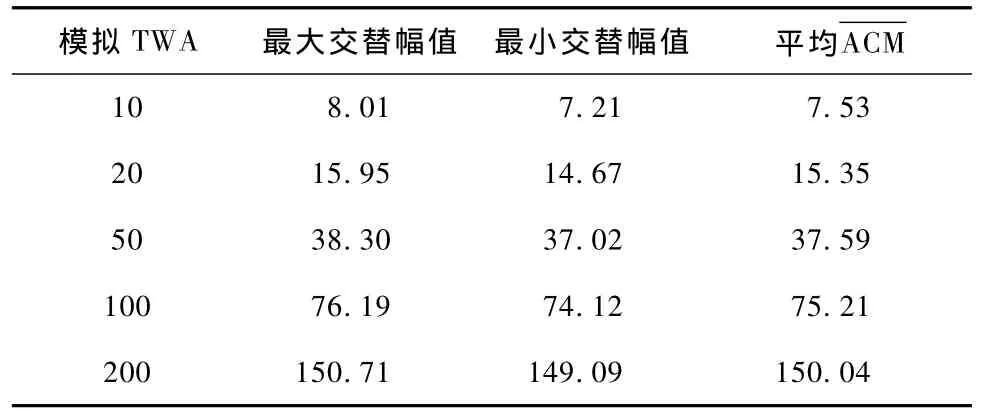
表2 T波交替水平分析Tab.2 TWA level analysis μV

由表2可见，相关计算测量出的TWA交替水平ACM约为实际TWA幅值的0.75倍，在此基础上，计算出在不同信噪比下测量模拟TWA的相关系数为0.99。

定义测量TWA的相对误差为

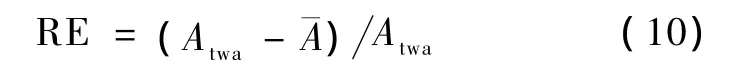
式中，Atwa为模拟的TWA幅值，为测量的TWA幅值。

在信噪比为30情况下，分别取 TWA=10，20，50，100，200 μV 下的任一模拟 ECG 信号。应用本算法量化分析TWA平均交替幅度，并引入Smith提出的SM法计算T波交替幅度ASM，对比分析结果如表3所示。

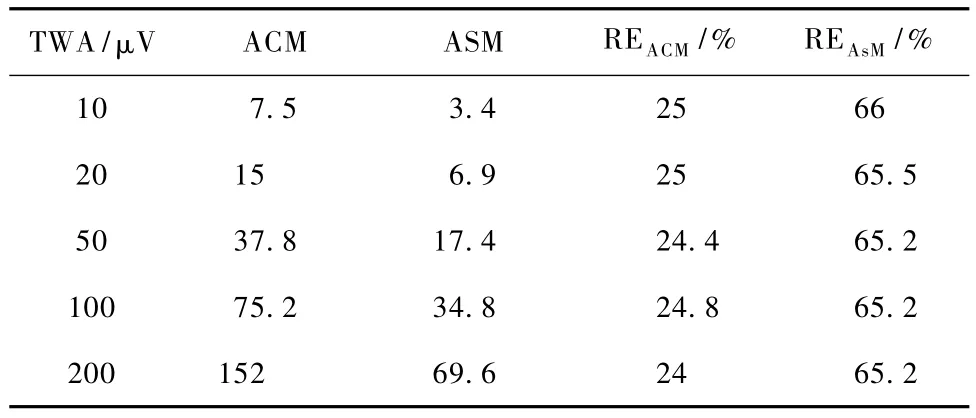
表3 TWA检测对比分析Tab.3 Comparision analysis of TWA detection

在模拟ECG情况下，本研究采用的分析法获得了较小的相对误差;在幅值评估方面，也是SM法获得的交替幅值的2.2倍，为TWA实际幅值的75%左右，更接近真实值。

2.2 临床评估

数据来源1:通过商用运动心电测试系统，从25名患有心肌梗塞或混合心绞痛的患者中，提取30 min时长的心电数据。

数据来源2:从心电研究的权威数据库——欧洲ST-T心电数据库和美国心脏猝死监护数据库(the sudden cardiac death holter database，SCDHD)中，各提取25段、30 min时长的患心绞痛、冠心病或心肌梗塞患者的ECG数据。

将这些数据划分为30个1 min时长的段，每段大致包含60～80个T波，对每个1 min时长的ECG分别运用本算法进行检测，同时也运用SM谱方法进行对比分析。统计分析结果为:本算法测量的平均TWA幅值约为SM方法测量值的2.2倍，两种算法对TWA幅值检测结果的相关系数为0.96，如图3所示。

部分样本检测结果如表4所示，其中编号为ECG1的1 min栏中的值“11(37%)”表明:被检测的30段ECG中发现11段出现 P＜0.05，这在一定程度上反映了TWA出现的频次。

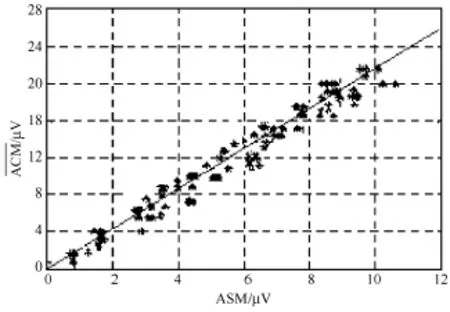
图3 本方法和SM法对临床数据TWA评估的相关性分析Fig.3 Correlation analysis of TWA estimation:the joint algorithm vs.SM

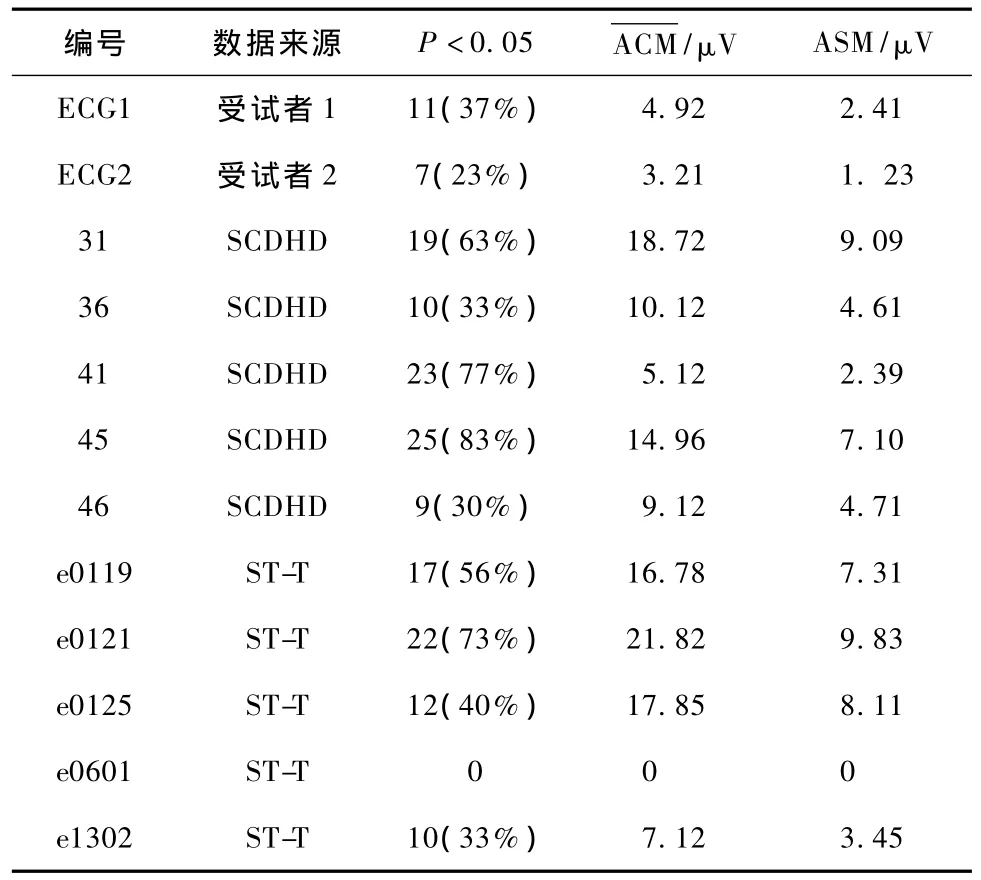
表4 部分样本的检测结果Tab.4 Test results of partial samples

表中编号 31、41、45、和 e0121的患者，其 TWA在多段心拍检测中出现的频率均高达70%以上。根据TWA是预测发生恶性室性心律失常和心脏猝死的预测指标观点，这些患者应被列为重点监测对象。

3 讨论

3.1 TWA分析的研究方向

TWA的量化评估难度很大，已有的各种算法都不同程度地存在缺陷［7］。新的 TWA算法必须既具有较高的抗噪性能，又具有动态跟踪非稳态TWA的能力。采用现代谱估计和时频分析的方法，或者结合频域方法和时域方法互补的特点，将是今后研究的方向［20］。

利用连续小波变换提取T波时频信息，在指定时频窗内计算T波能量谱并分段统一编秩后，运用Wilcoxon秩和检验这一统计分析方法来定性判断T波交替。在此基础上，对包含T波交替的信号段进行T波的时域相关分析，确定交替的频次和程度，提取时域量化指标。这一时频联合分析方法既可达到传统谱分析方法的准确性，也可分析T波序列的时频能量谱变化情况，确定TWA出现的时域范围，可以实现TWA时频特征参数的量化评估。

3.2 设计包含TWA的仿真ECG信号方案

TWA检测算法的有效性必须通过仿真实验来评估，因此设计合理的、包含TWA的仿真ECG信号方案，最大限度地模拟实际采集的临床数据，对算法有效性的检测至关重要。

首先，用单个心拍来采用合成ECG信号;然后，以高斯函数及其一阶导数的波形来拟合两种形态、不同幅值的T波交替因子，将这些不同的T波因子与合成ECG信号叠加;接着，从权威心电噪声数据库中提取临床获得的心电基线漂移、肌电噪声和电极移动噪声，与模拟生成的高斯噪声混合，使噪声完全覆盖真实采集的ECG信号所含的噪声;最后，将混合噪声与合成ECG叠加，构造不同信噪比的、含T波交替的模拟ECG信号。本研究提出的这一设计方案，最大程度地符合真实情况下所采集的不同ECG信号，使验证实验结果具有可信度，可作为其他TWA算法性能评估时的仿真实验设计参考。

4 结论

心电T波交替蕴含了丰富的病理信息，是目前对心脏猝死和恶性心律失常的危险性进行无创风险评估的指标，具有重要的研究价值。SM谱分析法能够从频域的角度定性判别TWA，但它不能获取TWA时域特征信息，因此仅从频域角度分析 TWA是不够的，TWA所包含的病理信息还有待更充分地发掘。

本研究将非参数检验的统计分析方法与连续小波变换、相关分析技术结合，提出一种新的 T波交替量化分析方法，不仅从能量和频率角度来定性反映TWA的交替情况，也利用TWA交替相关指数ACIi和平均交替幅值，从交替频次和交替幅值的角度，对 TWA进行了时域量化分析。仿真实验和临床对比实验的结果均表明:本研究提出的这一方法在TWA检测上可以达到传统谱分析方法的准确率，同时也可实现TWA的时频分析和基于相关技术的时域量化分析，获取TWA在特定时间范围内更丰富的TWA时频特征信息，也支持静息状况下采集的患者的ECG分析，这些特点均是目前谱分析法和时域分析法所不具备的。

参考文献

［1］Mark Estesl NA，Homoud MK，Link MS，et al.Assessment of risk forsudden cardiac death［J］. CurrentProblemsin Cardiology，2002，27(6):246－266.

［2］孟照华，宋平.心脏猝死发生的预测研究现状［J］.中国急救医学，2005，25(4):286－287.

［3］Garcia，Euler de Vilhena.T-wave alternans:reviewing the clinical performance，understanding limitations，characterizing methodologies［J］.Annals of Noninvasive Electrocardiology，2008，13(4):401－420.

［4］Quarta G，Marino L.The microvolt T-wave alternans test:an emerging tool for risk stratification of sudden cardiac death ［J］.High Blood Pressure＆ Cardiovascular Prevention，2007，14(4):213－219.

［5］Javed B，Angel L.The elusive scourge of sudden cardiac death［J］.Journal of American College of Cardiology，2007，49(13):1434－1437.

［6］Adam DR.，Smith JM，Akselrod S，et al.，Fluctuations in T-wave morphology and susceptibility to ventricular fibrillation［J］.Journal of Electrocardiology，1984，17:209－218.

［7］Martinez JP，Olmos S.Methodological principles of T wave alternans analysis:A unified framework［J］.IEEE Transaction on Biomedical Engineering，2005，52(4):599 －613.

［8］Smith JM，Clancy EA，Valeri CR，et al.Electrical alternans and cardiac electrical instability［J］.Circulation，1988，77(1):110－121.

［9］Nearing BD，Huang AH，Verrier RL.Dynamic tracking of cardiac vulnerability by complex demodulation of the T wave［J］.Science，1991，252:437 －440.

［10］Laguna P，Ruiz M，Moody G.B，et al.Repolarization alternans detection using the KL transform and the beatquency spectrum［J］.Computing in Cardiology，1996，23:673 －676.

［11］Nearing BD，Verrier RL，Modified moving average analysis of T-wave alternans to predictventricularfibrillation with high accuracy［J］.Journal of Applied Physiology，2002，92:541 －549.

［12］Burattini L， Zareba W， Moss AJ， Correlation method for detection of transient T-wave alternans in digital Holter ECG recordings［J］.Annals of Noninvasive.Electrocardiology.，1999，4(4):416－426.

［13］Ferdjallah M，Barr RE，Adaptive digital notch filter design on the unit circle for the removal of powerline noise from biomedical signals［J］.IEEE Transaction on Biomedical Engineering，1994:41(4):529－536.

［14］MeyerC， Keiser H. Electr，ocardiogram baseline noise estimation and removalusing cubic splinesand statespace computation techniques［J］. Computers and Biomedical Research，1977，10:459－470.

［15］万相奎，徐杜，张军.心电信号小波消噪方法的研究［J］.中国生物医学工程学报，2008，27(4):630－632.

［16］张津海，高小榕，曾乐朋.低采样率心电非稳态T波交替分析方法［J］.清华大学学报(自然科学版)，2003，43(9):1214－1217.

［17］Janusek D， Pawlowski Z. Comparison of T-wave alternans detection methods ［J］. Biocybernetics and Biomedical Engineering，2004，24(4):31－41.

［18］Martinez JP， OlmosS， Laguna P. Simulation studyand performance evaluation of T-wave alternans detector［C］//Proceedings of the 22”d Annual EMBS International Conference.Chicago，2000:2291 －2297.

［19］Inaki R，Neil R，Grubb，et al.T-wave alternans found in preventricular tachyarrhythmias in CCU patients using a wavelet transform-based methodology［J］. IEEE Transaction on Biomedical Engineering，2008，55(11):2658－2665.

［20］张石，佘黎煌，徐中强等，心电 T波电交替检测算法综述［J］.中国生物医学工程学报，2010，29(3):446－463.