上证指数波动率和收益率长期依赖关系的实证研究

王国治

(华南理工大学 金融工程研究中心，广东 广州 510006)

关于市场长期相关的问题，人们已针对不同的资产进行了研究，包括：股票指数、利率[1-2]、政府债券、汇率[3]。这些研究中运用了多种方法，大多数文献在解释长期相关是根据长期相关的特征参数即Hurst指数H和临界值0.5进行比较。但是，作为最普遍应用的Hurst指数H估计技术的重要部分，由于存在短期记忆效应所导致的偏差，如：在基础过程中的ARIMA和 (G)ARCH模型中的偏差现象，因此将这种解释长期相关的方法未经充分讨论就运用到长期相关的研究中是很成问题的。而且，短期相关和长期相关在投资组合选择、期权定价和风险管理这些重要的金融研究领域中有着不同的含义，所以对这两种类型的相关进行区分具有非常重要的意义。为处理这个问题，文章通过运用经典的和修正过的重标极差方法[4-5]结合具有预白和后黑的moving block bootsrap方法(以后简称MBB)对非长期相关的假设检验构建置信区间[6]，集中检验沪市A股上证指数的收益率和波动率的长期相关。数据集包括了1999-2009上证指数的数据。

一、长期相关

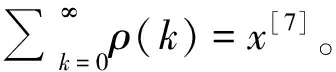
二、经典和修正的重标极差方法

重标极差分析(R/S)是最早的Hurst指数估计方法并由H.E.Hurst在1951年提出并由Mandelbrot和Wallis进行了修正。在这个分析过程中，将时长为T的连续收益率时间序列划分为N个相邻的时长为v的子时间间隔，即Nv=T。每个子时间间隔其统计特征的重标极差可以通过Ri/Si给出。这里Ri是相应统计特征的一个范围，Si是相应的收益率标准差。对每个时间子间隔都进行这样的处理[11]。重标极差可以写为

(R/S)v≈cvH

(1)

这里v是可以变动的而c是常量。上式在双对数坐标里显示出乘幂尺度[12]。为了揭示尺度变换，对上式两边取对数并运用普通ols估计出H。用探测周期的V统计量对Hurst指数进行平稳性检验，V统计量可以定义为

(2)

对于一个独立过程其收敛的分布定义为[4，5，11]

(3)

对于非长期相关过程，V若随着标度v的增加而递增或递减，那么V就分别是恒定的持续性或反持续性。这就是经典的R/S分析，因为具有短期记忆效应，Lo[5]提出了修正的重标极差分析M-R/S。它和经典方法的区别主要在于运用了修正过的标准差，这个标准差是通过从所选的从第一个子时间间隔到滞后的时间间隔ξ的原始时间序列中，运用原始时间序列的自相关协方差得出的，如下式

(4)

这样，R/S分析只是M-R/S分析当ξ=0的特殊情形。对于修正的重标极差估计来说，正确选择滞后非常关键[13-14]。Lo[5]根据原始序列ρ(1)的一阶自回归系数给出了最优滞后值。由下式给出(下式中的[.]是向下取整算符)

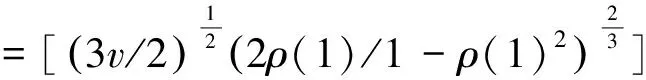
(5)

这可得到关于设定标度v的修正的重标极差估计量，并构建V统计量，从分布FV由非长期相关的虚拟假设得出临界值，将V统计量和临界值进行比较。

三、研究方法

Bootstrap方法用来处理小样本的统计特性。其基本含义就是将原始序列进行重整并对一个具体参数或统计量进行重复估计。通过序列重整，虽然原始序列的分布特性保持不变，但可能存在的相关关系会遭到扭曲[15]。由bootsrap方法估计出的置信区间进行假设检验。因为简单的bootstrap对时间序列的整理将短期相关和长期相关都消除了。因此，这种方法无法达成我们研究长期相关的目的。Srinivas和Srinivasan[6]给出了一个修正的bootstrap方法，即MBB，该方法保留了短期相关的特性但缺少长期相关。

四、数据

通过对上证指数收益率和波动率运用经典的和修正的重标极差分析法。设Ps，t是上证指数在t的收盘价，t=0，…，Ns这里Ns是上证指数的时间序列长度。上证指数在时间t的连续收益率可以表示为rs，t=log(Ps，t/Ps，t-1)其中t=1，…Ns。用收益率的绝对值来测度，对于上证指数在时间t的收益率测度表示为|rs，t︱，检验区间从1999/5/4～2009/5/14。基本统计描述由表1给出。从回报率的偏度和峰度来看不遵循正态分布。图1Q-Q概率图显示了这些特性。相对基于标准正态分布的方法[12]，从基本的统计分析结果可以看到运用boostrap方法构建置信区间的重要性并避免很多方法对不同分布所具有的敏感性。

表1 上证指数收益率的统计描述

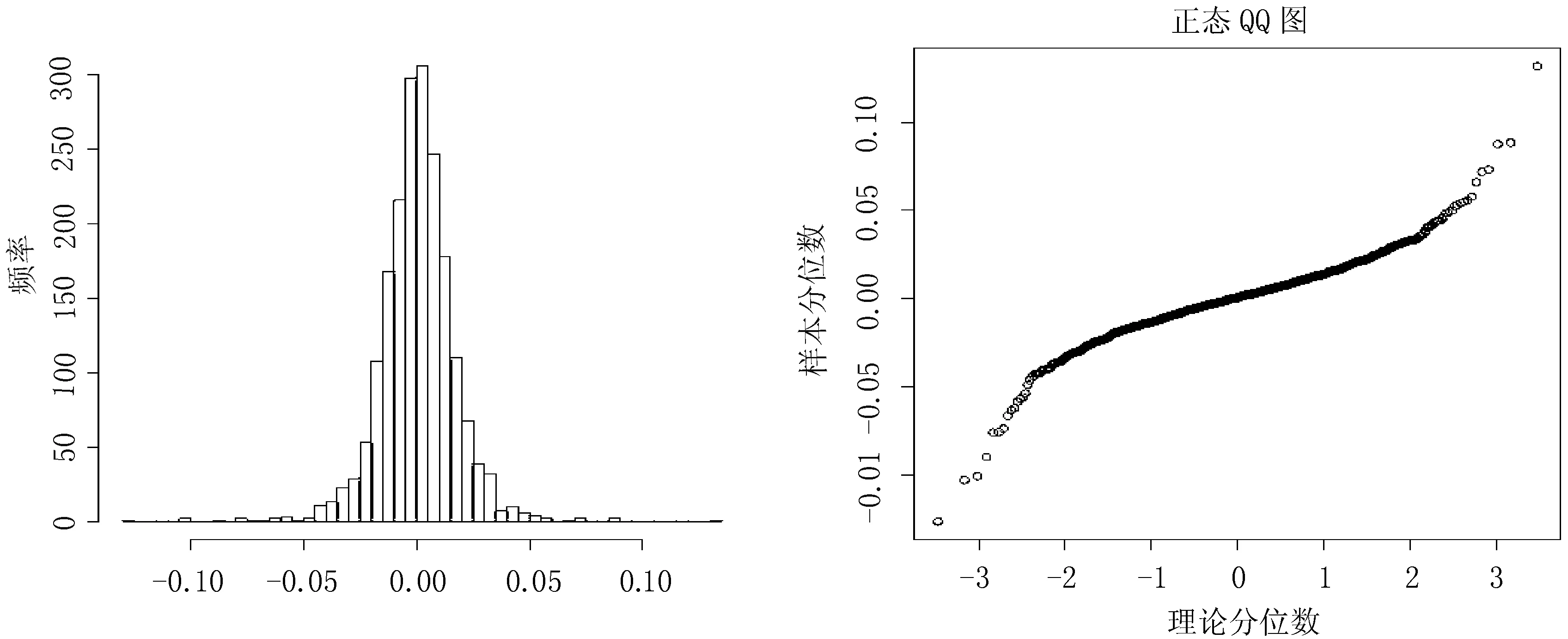
图1 上证指数的柱状图和QQ图

五、结果和讨论

表2给出由式(5)给出的最优滞后ξ*，对于收益率来说，最优滞后为4。对于波动率最优滞后的估计值为10。从滞后的估计可看出一方面上证指数的收益率不存在长期相关，另一方面波动率存在长期相关，这和一些关于新兴市场不够成熟效率不高导致存在持续性特征的研究相抵触[16]，但绝大多数研究都没有考虑要检验时间序列的统计特征，而是仅将Hurst指数H或V统计量和相应的临界值进行比较。因此这些结果应重新检测时间序列的统计特征和可能的短期相关。

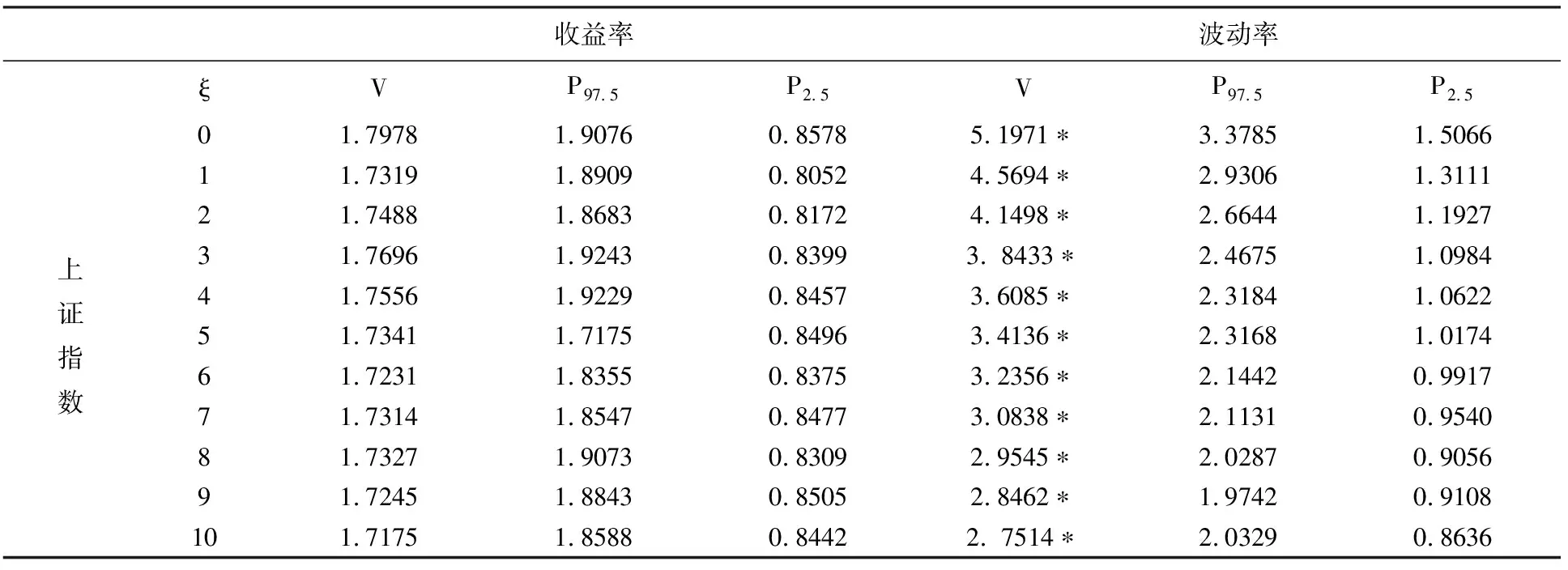
表2 V统计量和boostrap方法的置信区间

图2比较了分别由bootstrap和Lo[6]的方法得出的置信区间，其中Lo的方法只在滞后值选择正确时才是正确的。

从图2中可以看出，基于时间序列的收益率对所有检测的滞后值ξ来说，由bootstrap所得的置信区间和由Lo方法所得置信区间很接近，因为即使当ξ=0是这种情况也存在，所以短期相关或完全没有或者非常弱，并且经典R/S的估计是无偏的。对于波动率，两种方法所得置信区间直到滞后值在8和9之间才没有出现明显的冲突。对于较小滞后值，由于boostrap的临界值远大于Lo方法所得，那么最优滞后值就非(5)的结果而是当两种方法所得置信区间相等时为最优滞后值。运用R/S和M-R/S都得到拒绝收益率长期相关和接受波动率长期相关的假设检验的结果。这样看来，对于假设检验用MBB比用M-R/S可给出更重要信息。从所得结果可看到，如果正确的选择AR(1)，上证指数波动率不仅是短期相关而且也是长期相关。因为收益率没有发现有长期相关，ARFIMA模型就不适用。不过，波动率存在的短期和长期相关意味着运用诸如FIGARCH模型会比简单GARCH模型得到更好结果。波动率持续性显示外在冲击幅度以双曲衰减，比一般GARCH模型隐含的衰减幅度要慢。

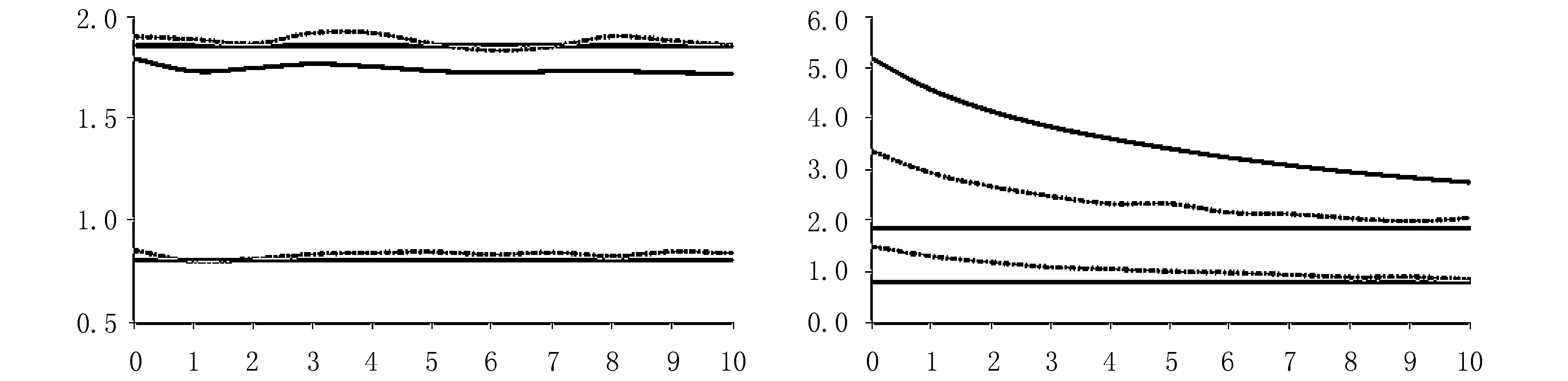
图2 收益率(左)和波动率(右)的V统计量的估计值

六、结论

本文研究了1999 到2009上证指数收益率和波动率长期相关的存在问题。我们选择经典的和修正过的重标极差方法根据V统计量来检验长期相关。为避免潜在的短期相关，分布敏感性，异方差和趋势这些复杂情况，运用具有预白和后黑的MBB方法构建假设检验的置信区间。显示上证指数的收益率不存在显著的长期相关而波动率存在显著的长期相关，并同时存在显著的短期相关。另外，我们讨论了从修正重标极差方法中找出最优滞后值的可能性。对于收益率来说所得结果和已有的一些认为中国股票市场具有持续性的研究相抵触。[16]这些研究大多数没有运用置信区间或只基于标准正态分布的置信区间。因此，研究的结果需要从新检验和从新进行解释。

参考文献：

[1]Cajueiro D，Tabak B.Long-range dependence and multifractality in the structure of libor interest rates[J].Physica A, 2007，373: 603-614.

[2]Di Matteo T.Multi-scaling in finance[J].Quantitative Finance，2007(1)：21-36.

[3]Vandewalle N，Ausloos M，Boveroux P.Detrended fluctuation analysis of the foreign exchange market[C].Budapest，Hungary：Econophysic，1997.

[4]Hurst H.Long term storage capacity of reservoirs[J].Transactions of the American Society of Engineers, 1951，116: 770-808.

[5]Lo A.Long-term memeory in stock market prices[J].Econometrica，1991，59(5): 1279-1313.

[6]Srinivas V，Srinivasan K.Post-blackening for modeling dependent annual streamflows[J].Journal of Hydrology, 2000，230: 86-126.

[7]Beran J.Statistics for Long-Memory Processes，Volume 61 of Monographs on Statistics and Applied Probability[M].New York：Chapman and Hall，1994.

[8]Lillo F，Farmer J.The long memory of the efficient market[J].Studies in Nonlinear Dynamics and Econometrics, 2004，8(3): 1-15.

[9]Embrechts P，Maejima M.Selfsimilar Processes[M].Princeton：Princeton University，2002.

[10]Mandelbrot B，Wallis J.Joah，joseph and operational hydrology[J].Water Resources Research, 1968(4): 33-57.

[11]Peters E.Fractal Market Analysis-Applying Chaos Theory to Investment and Analysis[M].New York：John Wiley&Sons，Inc，1994.

[12]Weron R.Estimating long-range dependence：finite sample properties and confidence intervals[J].Physica A, 2002，312(1-2): 285-299.

[13]Teverosky V，Taqqu M，Willinger W.A critical look at lo's modified r/s statistic[J].Journal of Statistical Planning and Inference, 1999，80(1-2): 211-227.

[14]Wang W，van Gelder P，Vrijling J，et al.Detecting long-memory：Monte carlo simulations and application to daily streamflow processes[J].Hydrology And Earth System Sciences Discussions, 2006(3): 1603-1627.

[15]Davison A，Hinkley D.Bootstrap Methods and Their Application[M].Cambridge：Cambridge University Press，1997.

[16]Los C A，Yu B.Persistence characteristics of the Chinese stock markets[J].International Review Of Financial Analysis，2008(1)：64-82.