数据挖掘技术在松花江水质预测中的应用

赵 英，崔福义，郭 亮

(哈尔滨工业大学城市水资源与水环境国家重点实验室，150090 哈尔滨，zhaoying@hit.edu.cn)

数据挖掘技术在松花江水质预测中的应用

赵 英，崔福义，郭 亮

(哈尔滨工业大学城市水资源与水环境国家重点实验室，150090 哈尔滨，zhaoying@hit.edu.cn)

为更好地实现松花江水质预测，对水质的科学管理起到指导作用，应用人工神经网络技术(ANN，Artifical Neural Networts)，利用松花江四方台监测站某连续3年水质数据，建立水质预测模型，实现对松花江主要污染指标CODMn的预测.为保证预测模型具有较高的预测精度，将数据按月分期，应用聚类分析法对数据进行处理，剔除异常数据，使有效数据能够均匀分布.并通过测试研究验证聚类分析法处理数据后对预测精度的影响效果.结果表明，将聚类分析法应用到水质预测中后，可较大地改善模型预测效果，成绩显著.

水质预测;预测模型;聚类分析法;人工神经网络

近年来，随着我国工业化以及城镇化进程加快，全国各地流域环境遭受不同程度污染，对人体健、生态安全以及生产和生活构成重要影响.松花江流域干流为沿江城市的主要饮用水源，监测数据表明，目前水质污染状况非常严重，已对吉林省、黑龙江省生态环境和人民生产生活造成了重大影响.面对新的形势和要求，目前我国流域环境监测、水质预测等技术方法与环境污染的客观要求已明显滞后.因此，研发应对水环境监测、预测新方法，提高科学的环境管理和综合决策能力，在今后很长一段时期是十分紧迫和必要的.

2002～2006年松花江水域水质状况见表1.可以看出，2002～2006年劣Ⅴ类水质所占的百分数总体呈上升趋势，由此可知松花江水域水质污染状况有加重的趋势，可见建立松花江水域的预测模型，探讨未来水质的变化情况具有一定意义，对于松花江水域的管理、防治水污染、确保饮用水安全起到积极的作用.从主要污染指标一栏中可以看出，2002～2006年5年中主要污染指标包含CODMn、石油类、氨氮、生化需氧量、挥发酚，其中CODMn连续5年出现，可见CODMn的超标是造成松花江水域污染的最主要因素，因此，确定以 CODMn为预测对象.

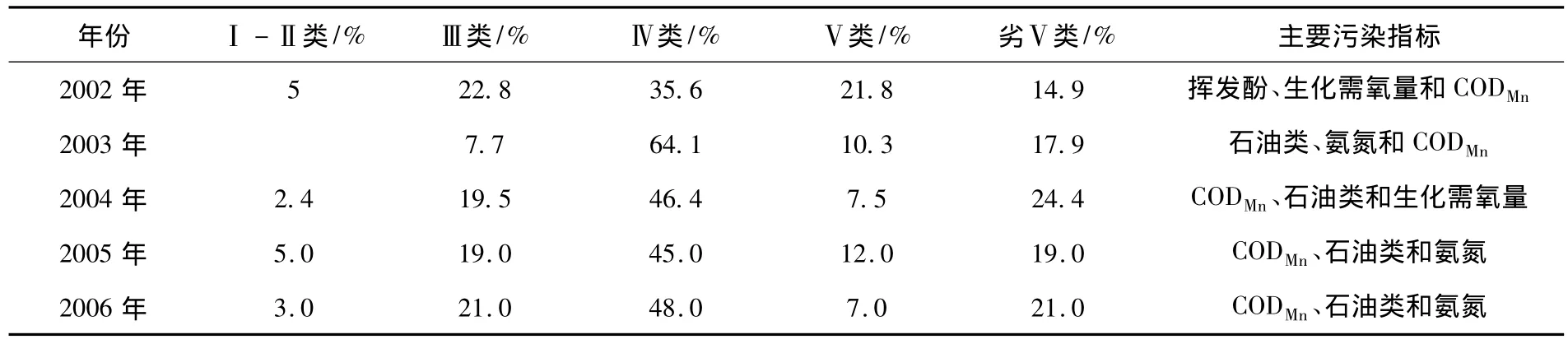
表1 2002－2006年松花江水域水质类别分析和主要污染指标对比

在综合分析松花江主要污染指标、水厂日常检测的原水水质参数种类、课题实际需要以及对CODMn值产生影响等因素后，确定水温、浊度、色度、pH值、氨氮、亚硝酸盐、电导率、碱度、水流量9种水质参数为CODMn的影响因子.除此之外任何水质参数的变化都是连续的，因此，也将当日的CODMn作为影响因子，以10种影响因子预测次日的CODMn.

1 实验方法

1.1 数据处理方法的选择

数据挖掘技术有很多种，但其在水质预测领域中的应用并不多.分析本文水质数据的特点，就单个水质参数而言，这些数据变化幅度不大，且都是正实数，不包含向量等复杂数据，并且数据为日监测数值，频度不大.聚类分析法是数据挖掘技术中较常用的一种方法，处理过程简单易懂，实用性较强.因此，综合本文数据特点选择聚类分析法即可以方便地解决数据处理的问题，达到预期效果［1－4］.

聚类分析是依据样本间关联的度量标准将其自动分成几个类，且使同一类中的样本相似，而属于不同类的样本相异的一组方法.一个聚类分析系统的输入是一组样本和一个度量两个样本间相似度(或相异度)的标准，聚类分析的输出是数据集的几个类(簇)，这些类构成一个分区或分区结构.聚类分析的一个附加结果是对每个类的综合描述，这种结果对于进一步深入分析数据集的特征尤为重要.这样应用聚类分析法可以将水质数据中的离群数据即异常数据剔除掉，提高预测模型精度［5－9］.

1.2 聚类分析法应用分析

聚类分析可以根据聚类中心点来进行数据筛选，一方面可以剔除孤立点，另一方面还可以剔除一些距离中心点过远的异常数据，不仅可以剔除异常数据，还可以使过滤后的数据具有良好的规范性［10－13］.

在选择研究数据时，剔除的是预测模型中对预测对象有影响的水质参数的异常值.根据上节确定的影响因子，水温、浊度、色度、pH值、氨氮、亚硝酸盐、电导率、碱度、水流量9种水质参数均为聚类分析对象，此外训练时预测对象的数据也可能存在异常，因此，将次日的CODMn值也作为聚类分析对象，即本研究共计10组研究数据.

本文现有包含以上10组水质参数的松花江四方台监测站某连续3年日检测数据1 028组，因为每个月份的数据均具有不同的水质特点，按照月份分期，首先选取K－平均算法进行聚类分析，剔除样本数目过少的类，因为将每个月的数据分成3组(按3年的划分)，在计算中，如果每组的数据样本数少于该月样本总数的10%，剔除该类，并重新进行划分计算.接着对样本与中心之间的距离进行分析，剔除距离较远的样本，采用欧式距离进行计算，剔除所有距离大于500的异常样本点，从而使所获得的数据具有较好的规范性.

1.3 处理过程及结果分析

应用聚类分析法时采用SPSS(Statistical Package for the Social Science)软件，其是目前世界上最著名的数据分析软件.SPSS最突出的特点是操作界面极为友好，使用Windows的窗口方式即可展示各种管理和分析数据方法的功能，使用对话框就可展示出各种功能选择项，无需编程，只根据需要进行图形用户界面操作就可以实现数据的分析和处理.

在本文聚类分析研究中采用K－平均算法，其具体流程如下:

1)任意选择3个样本作为初始类的中心;2)根据类中对象的平均值，将每个样本重新聚合到最类似的类;3)更新类的平均值，即计算每个类中样本的平均值，将其作为中心点;4)重复2)、3)直到不再发生变化.

使用K－平均算法进行聚类，根据各个类的样本数目来剔除孤立点.第一次聚类结果见表2.

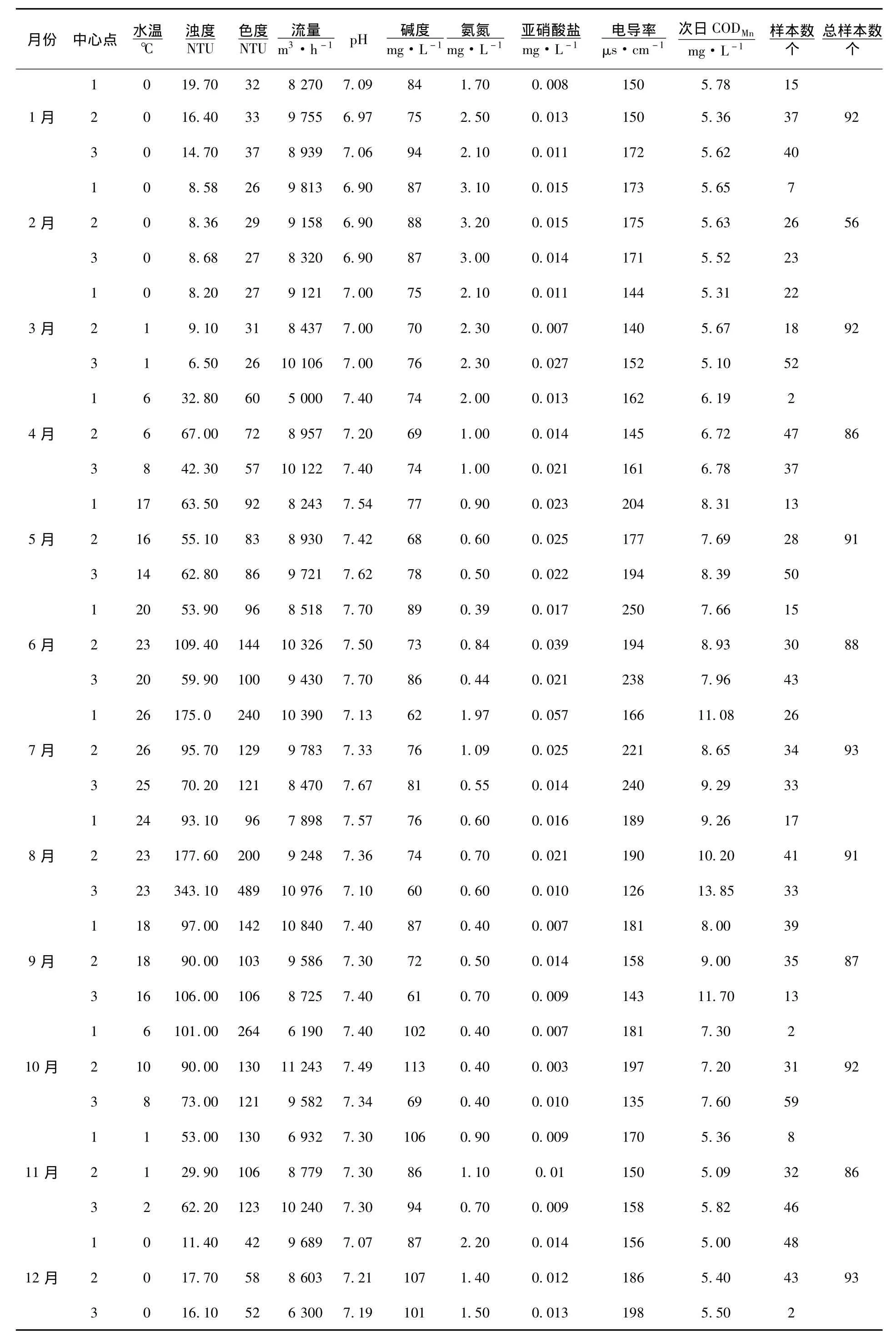
表2 K－平均算法聚类结果(1)

从表2中选取类样本数少于该月总样本数10%的类，进行剔除，选取的类分别是4月类1、10月类1、11月类1、12月类3.剔除这些类，并对4月、10月、11月、12月重新进行聚类.得到的结果如表3所示.

躺着想了许久才发现面膜还没洗，该死，又过时间了，脸上的水分都被吸走了。就像他死后，我的感情也被有他在的那段时间吸走了。

分析表3注意到4月类2样本数目仍然少于该月样本总数10%的类，剔除该类，重新对4月数据进行聚类计算，结果如表4所示.

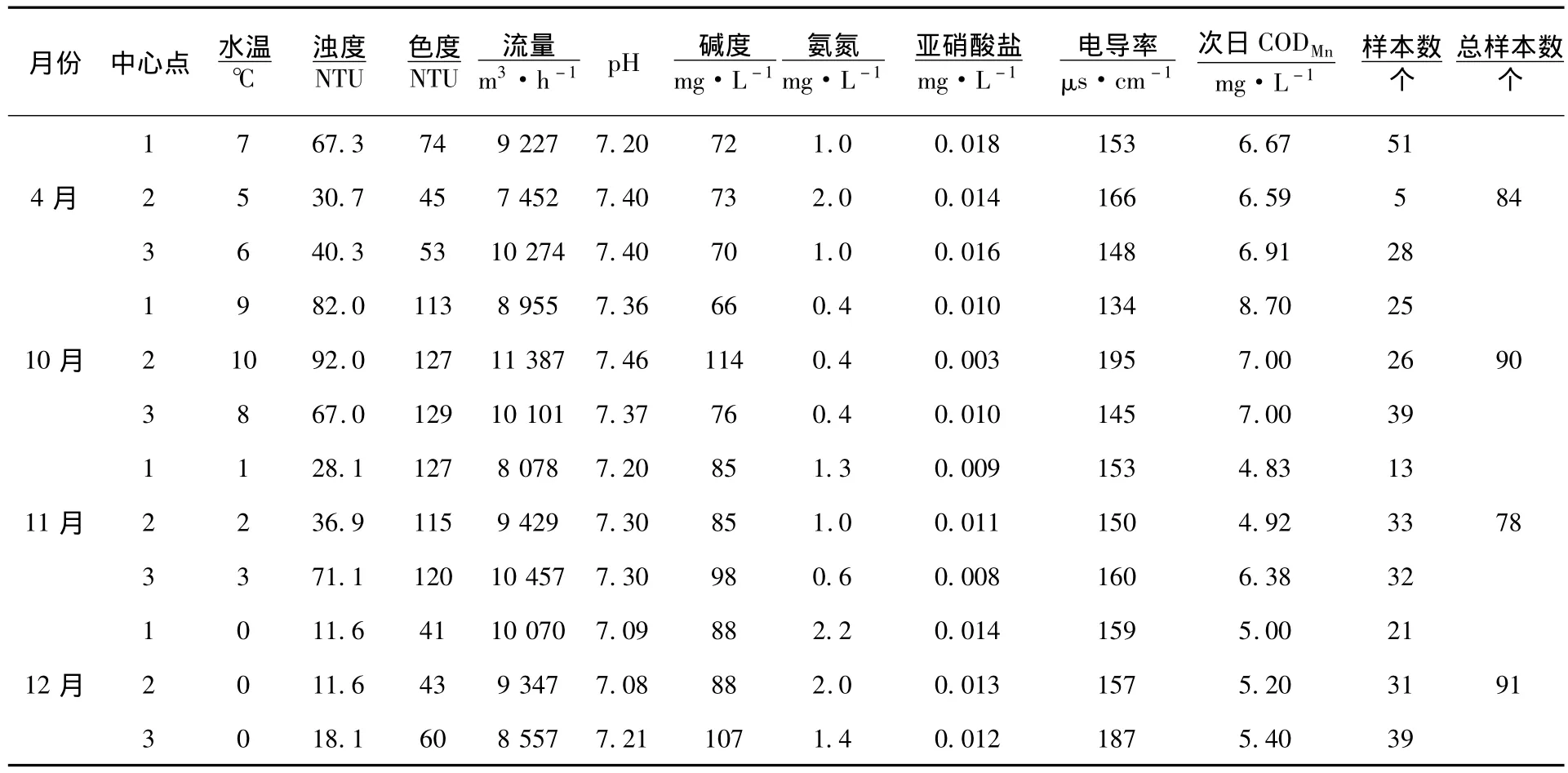
表3 K－平均算法聚类结果(2)

表4 K－平均算法聚类结果(3)

至此，获得了36个可以表征各个月特征的聚类中心点.以这些中心点为中心，计算所属类内各样本Xi与中心点X0的距离，采用欧式距离进行计算，剔除所有di≥500的异常样本点.

在剔除数据的同时考察剩余样本的个数.其中m为剔除后该月剩余样本数目.剔除情况如表5所示.

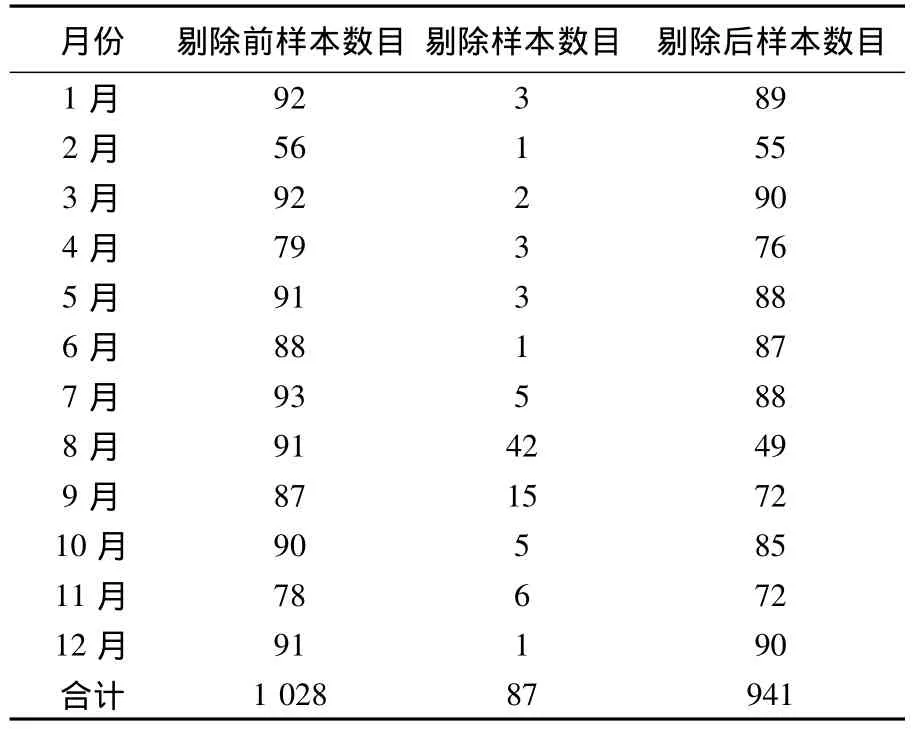
表5 K－平均算法聚类后样本分布情况(1) 个

从表5可以看出，8月份与9月份样本被剔除的最多，8月份剔除样本数达本月监测个数的46%，9月份为17%.由于水质的变化相当复杂，受很多因素影响，本文在剔除异常数据时是以水域某一时段(某月)内的通常状况为标准，对于非正常状态下对水域的影响因素考虑较少，为避免过多地删除数据，规定在某一时段内(某月)因机械或人为等因素产生一些异常数据不应该大于本时段内所监测数据个数的10%，若大于这个值，说明该月可能存在一些水质异常变化，这些值虽然偏离常规状态下的监测值，但也是水质真实状况的反应，不应该予以剔除.在8、9月份初步得到的异常值都大于10%，再次对这两个月的数据进行处理，将剔除所有di≥800的异常样本点，减少剔除异常数据数目，避免删除反映水质真实状况的数据.剔除情况如表6所示.

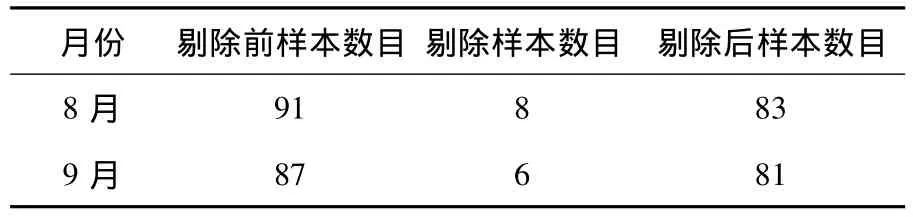
表6 K－平均算法聚类后样本分布情况(2) 个

表6中8、9月份的剔除样本数均小于该月监测个数的10%.剩余样本总数为984.

2 水质预测模型的建立

2.1 预测方法的选择及可行性分析

经过综合分析认为:人工神经网络模型属于一种黑箱模型，其在没有明确提供给过程内部的物理演化过程知识的情况下，也可以在一个过程的输入与输出之间直接建立关系，即使这些数据中含有噪声或错误［14－15］.这些特性说明ANN网络非常适合复杂的松花江水质预测模型的建立，可以帮助进一步捕捉、探索其水质演变过程中的规律.并且神经网络的建模过程非常灵活，可以采用不同的非线性函数来模拟其过程的非线性特征.因此，确定选择人工神经网络技术作为本文的建模方法.

2.2 应用MATLAB建立网络模型

MATLAB是美国Mathworks公司1982年推出的数学软件，它具有强大的数值计算能力和优秀的数据可视化能力［16］.其提供的神经网络设计与仿真GUI，是进行神经网络系统分析与设计的绝佳工具，使用户能够方便地通过图形用户界面进行神经网络的建模与仿真，无需编程.本文应用MATLAB的GUI功能实现建模与仿真.

模型规模较大，不便于训练，也会降低网络的性能.理论已经证明，具有单隐层的BP神经网络模型，当隐层神经元数目足够多时，可以以任意精度逼近任何一个具有有限间断点的非线性函数［17］，因此，本文建立的是单隐层BP神经网络.

由于影响因子共有10项，模型输入有10个变量，预测对象是次日的CODMn，即输出为1个变量.对于隐含层神经元个数的确定，有很多文献介绍了一些方法，但只是一些经验方法，并不具有权威性，并且针对不同水域、不同情况的预测模型，即使输入、输出变量相同，当达到最佳预测效果时，其隐含层神经元个数都不一定是相同的.因此，根据经验，隐含层分别从10～20选值，同时在选择隐含层神经元传递函数时，分别选用LOGSIG和TANSIG函数.BP网络最后一层神经元的特性决定了整个神经网络的输出特性.当最后一层神经元采用Sigmoid型函数，整个网络的输出就被限制在一个较小的范围内;如果最后一层神经元采用PURELIN型函数，则整个网络输出可以取任意值，因此，选择输出层的神经元传递函数为PURELIN.

在确定好上述参数和函数后，应用MATLAB的GUI工具建立网络模型.图1是建立的网络模型之一.

因为隐含层神经元个数分别选择从11～20，神经元传递函数分别选择LOGSIG和TANSIG函数，这样就根据隐含层神经元个数和传递函数的不同建立20种模型，分别应用不同的训练集数据进行训练，选择最优模型作为预测模型.

3 聚类分析法应用效果分析

为考察聚类分析法对数据处理的效果，对其处理后得到的结果应用到水质预测模型中，并与未经过处理的数据进行对比，考察其应用效果.

3.1 传统方法预测精度

由于未应用聚类分析法处理数据，有效数据共有1 028组，经划分得到训练集数据992组，测试集数据36组.

利用上述训练集数据，应用MATLAB软件建模，经过对比分析，得到最优模型结构为隐含层神经元个数为16，传递函数是TANSIG，将其作为预测模型.

为了使模型测试结果具有一致性和普遍性，测试集选用前文某连续3年中其中1年每月1、2、3日的监测值，若某一日的值不存在，则选用顺延日期的监测值，这样每月3组数值，共形成36组测试集.应用预测模型对测试集数据进行预测研究，得到的预测值与实测值结果如表7所示.

CODMn预测值与实测值对比曲线和误差曲线如图2，3，图中的预测时间从1月开始至12月止，时间顺序与表7中的时间顺序相同.

在对比曲线中，对预测值与实测值二组数据进行相关性分析，可知相关系数为0.886.通过对预测误差曲线中的数据进行分析可以得出:最大预测误差为11.61%，最小预测误差为1.18%，平均预测误差为4.76%.

表7 传统方法CODMn预测值与实测值 mg·L－1

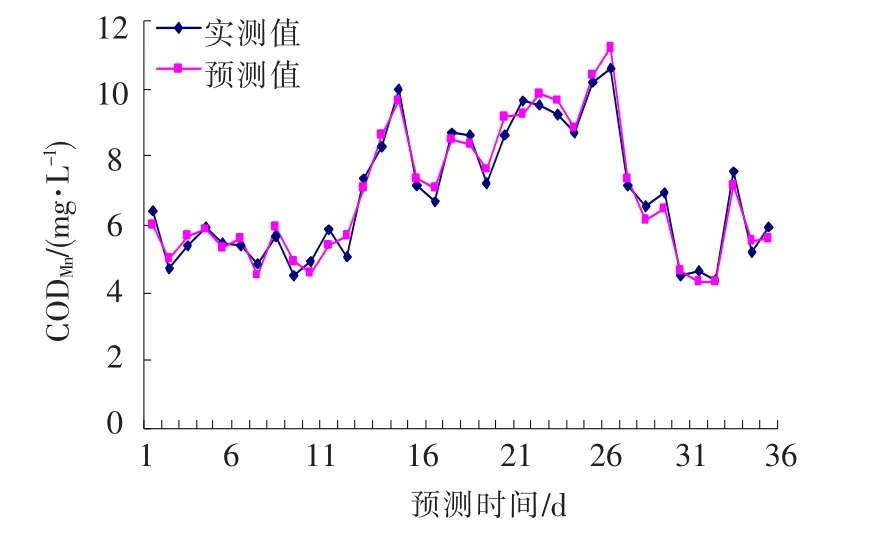
图2 CODMn预测值与实测值对比曲线

3.2 聚类分析法预测精度

应用聚类分析法处理数据后得到有效数据984组，划分成训练集数据948组，测试集数据36组，为了使对比具有同等性，测试集数据与前文相同.

应用MATLAB软件建模，经过对比分析得到最优预测模型结构为隐含层神经元个数19，传递函数是LOGSIG，将其作为预测模型.

应用预测模型对测试集数据进行预测，得到的预测值与实测值结果如表8所示.

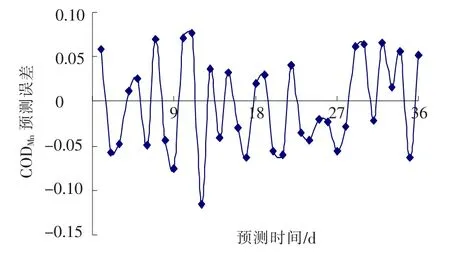
图3 CODMn预测误差

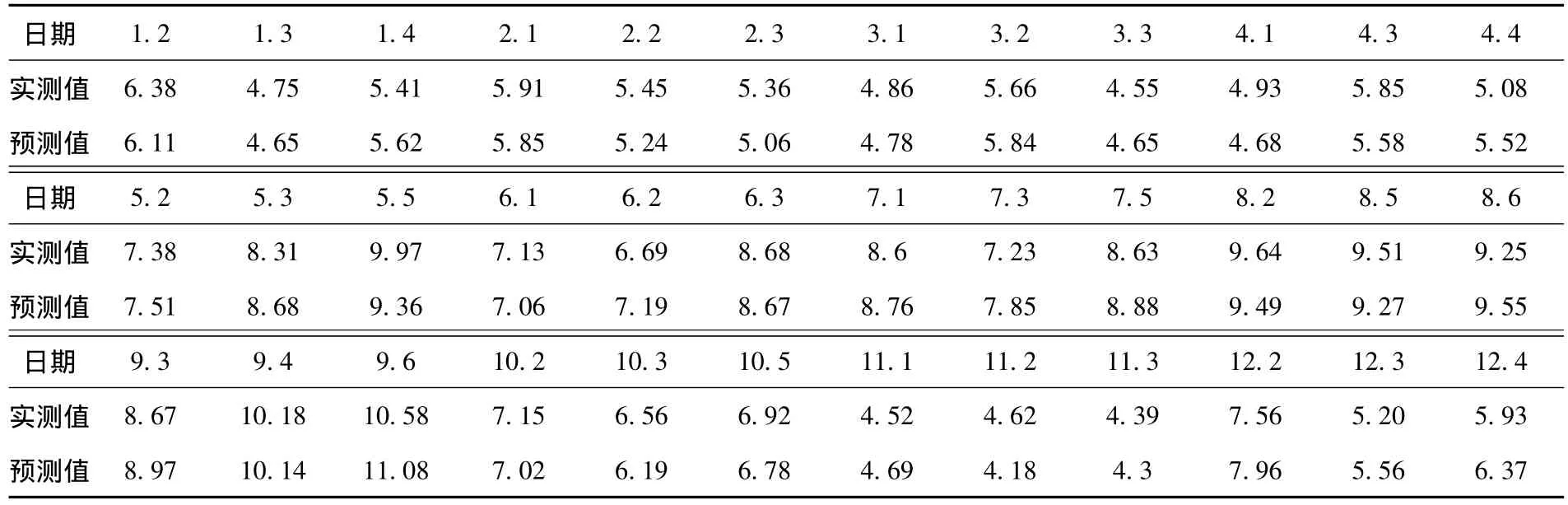
表8 聚类分析法应用后CODMn预测值与实测值 mg·L－1

CODMn预测值与实测值对比曲线和误差曲线如图4，5，图中的预测时间从1月开始至12月止，时间顺序与表8中的时间顺序相同.在对比曲线中，对预测值与实测值二组数据进行相关性分析，可知相关系数为0.925.通过对预测误差曲线中的数据进行分析，可以得出:最大预测误差为9.52%，最小预测误差为1.15%，平均预测误差为3.91%.

3.3 实验结果分析

从以上的对比研究可以看出，应用聚类分析方法对训练数据进行处理后，预测模型的预测效果得到较大提高.比较两者预测值与实测值的相关系数，可知应用该方法后的相关性要明显好于应用前;后者比前者最大预测误差降低了2.09个百分点，可见数据经过处理后，偏离聚类中心的异常点被删除掉，因此，最大误差降低很多;两者的最小预测误差几乎接近，是因为聚类过程中保留了离中心点位置较近的所有数据，并不影响预测的最小误差;从整体效果上看，数据经过聚类处理后离聚类中心点的平均值要小，因此，后者的平均误差比前者小，从数据上看降低了0.85个百分点，可见将聚类分析法应用到水质预测中可较大地改善模型预测效果，成绩显著.

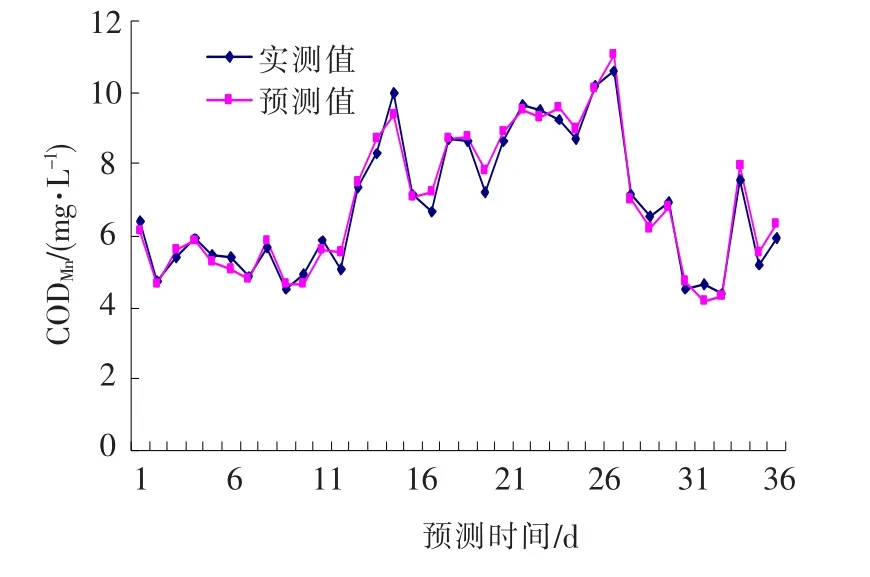
图4 CODMn预测值与实测值对比曲线

图5 CODMn预测误差

4 结语

本研究将数据挖掘技术、人工神经网络技术引入到水质预测模型研究中，可实现对地表水体的水质预测.本研究成果不仅可应用到松花江四方台监测站，也可以推广到其他地表水体的任何水质参数的水质预测中，为地表水体水质预测提供有效的方法，从而为水厂的安全、正常生产提供借鉴和指导.

［1］MASTROGIANNIS N，BOUTSINAS B，GIANNIKOS I.A method for improving the accuracy of data mining classification algorithms［J］.Computers ＆ Operations Research，2009，36(10):2829 －2839.

［2］YIN Yunfei.A proximate dynamics model for data mining［J］.Expert Systems with Applications，2009，36(6):9819－9833.

［3］CHU B，TSAI M，HO C.Toward a hybrid data mining model for customer retention［J］.Knowledge－ Based Systems，2007，20(8):703 －718.

［4］廖晓玉.空间数据挖掘在地表水水质评价与预测中的应用研究［D］.长春:东北师范大学，2006.

［5］DIXON M，GALLOP J R，LAMBERT S C，et al.Data mining to support anaerobic WWTP monitoring［J］.Control Engineering Practice，2007，15:987 －999.

［6］EL－SEBAKHY E A.Data mining in forecasting PVT correlations of crude oil systems based on type－1 fuzzy logic inference systems［J］.Computers ＆ Geosciences (2008)， doi:10.1016/j. cageo.2007.10.016.

［7］YANG Yubin，LIN Hui，GUO Zhongyang，et al.A data mining approach for heavy rainfall forecasting based on satellite image sequence analysis［J］.Computers＆ Geosciences，2007，33:20－30.

［8］SENCAN A.Modeling of thermodynamic properties of refrigerant/absorbent couples using data mining process［J］.Energy Conversion and Management，2007，48:470－480.

［9］CHEN Qiuwen，MYNETT A E.Integration of data mining techniques and heuristic knowledge in fuzzy logic modelling of eutrophication in Taihu Lake［J］.Ecological Modelling，2003，162:55 －67.

［10］SHAW M J，SUBRAMANIAM C，TAN G W，et al.Knowledge management and data mining for marketing［J］.Decision Support Systems，2001，31:127 －137.

［11］GIBERTA K，SPATE J，SANCHEZ－MARRE M，et al.Chapter twelve data mining for environmental systems［J］.Developments in Integrated Environmental Assessment，2008，3:205 －228.

［12］周东华.数据挖掘中聚类分析的研究与应用［D］.天津:天津大学，2006.

［13］GELBARD R，CARMELI A，BITTMANN R M，et al.Cluster analysis using multi－ algorithm voting in cross－ cultural studies［J］.Expert Systems with Applications，2009，36(7):10438 －10446.

［14］MAIER H R，MORGAN N，CHOW C W K.Use of artificial neural networks for predicting optimal alum doses and treated water quality parameters［J］.Environmental Modelling ＆ Software，2004，19(5):485 －494.

［15］SHETTY G R，MALKI H，CHELLAM S.Predicting contaminant removal during municipal drinking water nanofiltration using artificial neural networks［J］.Journal of Membrane Science，2003，212(1/2):99 －112.

［16］张宜华.精通MATLAB5［M］.北京:清华大学出版社，1999.

［17］庄镇泉，王熙法.神经网络与神经计算机［M］.北京:科学出版社，1994:100 －112.

Application of data mining technology in water quality forecast of Songhua River

ZHAO Ying，CUI Fu-yi，GUO Liang

(State Key Laboratory of Urban Water Resource and Environment，Harbin Institute of Technology，150090 Harbin，China，zhaoying@hit.edu.cn)

To better achieve water quality forecast of Songhua River and instruct scientific management of water quality，a water quality forecasting model is set up by ANN technology and is trained by water－quality data from Sifangtai Monitoring Station of the Songhua River.The model could be applied to forecast CODMnthat is one of the main pollution indicators in Songhua River.To improve forecasting accuracy，the data is divided into 12 groups and handled by excluding abnormal data based on clustering analysis.At last a test is carried out to verify the effect of clustering analysis，and the results indicate that the clustering analysis in waterquality forecasting model can improve the forecasting effect significantly.

water quality forecast;forecasting model;clustering analysis;artificial neural networks

X321

A

0367－6234(2011)10－0033－07

2010－05－21.

中国博士后基金资助项目(20110491056);黑龙江省博士后基金资助项目(LBH－Z10172);2011年哈尔滨工业大学科研创新基金资助项目.

赵 英(1978—)，女，博士，讲师;

崔福义(1958—)，男，教授，博士生导师.

(编辑 刘 彤)