基于分段斜槽技术的电机斜槽特性分析

梁文毅 陆天雄 张 翔

（杭州易泰达科技有限公司 杭州 310008）

1 引言

电机斜槽技术由于可有效改善电机响应性能在各类电机中广泛应用。对于电机斜槽的分析研究，目前普遍采用的是三维有限元法，其最大缺点是计算量极其庞大，对计算机性能要求过高。为解决该问题，相关文献提出了在二维有限元中采用分段斜槽进行异步电机斜槽分析的方法[1]，但是对于影响计算精度的分段方式和分段数没有进行相关理论分析。

本文阐述了在电磁场有限元仿真软件EasiMotor中，采用分段斜槽技术，成功解决了各类电机的斜槽分析功能。在此基础上，对电机斜槽的分段方式、分段数进行深入分析，详细讨论了分段数对计算精度的影响，并给出了相关结论。

2 分段斜槽技术原理

对于普通直槽电机内二维时变电磁场的定解问题，其数学描述可表示为[2]

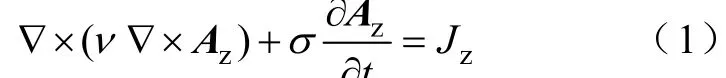
电机内电路方程为

电机的转矩平衡方程为

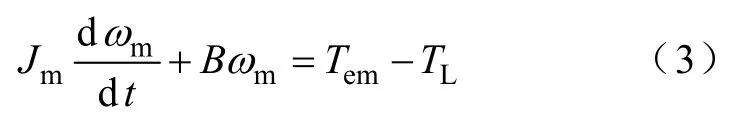
式中Az——矢量磁位；

Jz——传导电流密度；

Rs——绕组电阻；

Lσ——绕组漏抗；

ψs——绕组磁链；

Jm——转动惯量；

B——摩擦系数；

TL——负载转矩；

Tem——电磁转矩，采用Maxwell张量法求解。

对于斜槽电机，在EasiMotor中采用分段斜槽原理[1,3]进行分析。假设将斜槽电机轴向均匀分为n段，则对于其中任意第i段，式（1）可改写为

对于电压方程，可以改写为

采用有限元网格剖分，将式（4）离散化求解[2,4]，并结合式（3）～式（6）可以求解斜槽电机的各类时变问题。

3 分段对计算精度的影响

分段方式和分段数多少对斜槽电机电磁场性能分析产生关键影响。分段数越多，越接近实际斜槽情况，但是计算量也将大幅度增加。

在有限元求解中，反电动势与电磁转矩的准确求解是计算精度的保证，因此以下的分析中， 针对电磁转矩和反电动势的计算精度，进行分段方式和分段数的选择分析。

3.1 忽略齿槽效应时的分段模型

为分析分段对计算精度的影响，作如下假设：①电机斜槽角度为电角度β；②不考虑电机开槽对磁场的影响；③绕组电流以集中电流进行考虑。

假设某一时刻电机的磁场分布如图1所示，纵坐标表示电机基波磁场的空间分布，电流I为单位电流，导条（或者绕组）轴向投影长度L为单位长度，导条运行速度v为单位转速，则此时导体在该磁场下的转矩、反电动势可统一表示为

图1 电机斜槽分段模型Fig.1 Multi-slices model of skew motor

采用分段斜槽时，设电机轴向分段数为n，则此时导体在该磁场下的转矩、反电动势可统一表示为

而对于任意μ次谐波，该式可表示为

3.2 分段方式对收敛速度的影响

在文献[3]中提到了当轴向分段数为n段时，其每一段的斜槽角度取为

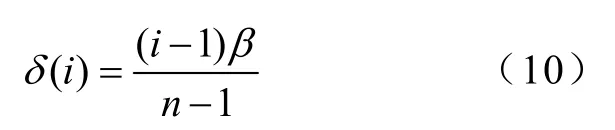
用图表示该分段方式，如图2a所示（方式1）。这里对另外一种轴向分段方式进行分析，如图2b所示（方式2），取每一段的斜槽角度为

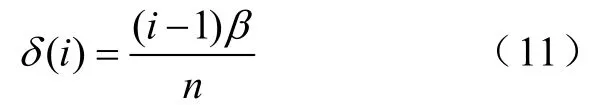
图2 轴向分段方法比较Fig.2 Demonstration of two slice methods

当采用图2a分段方式时，式（8）可以整理为

而当采用图2b分段方式时，式（8）可以整理为

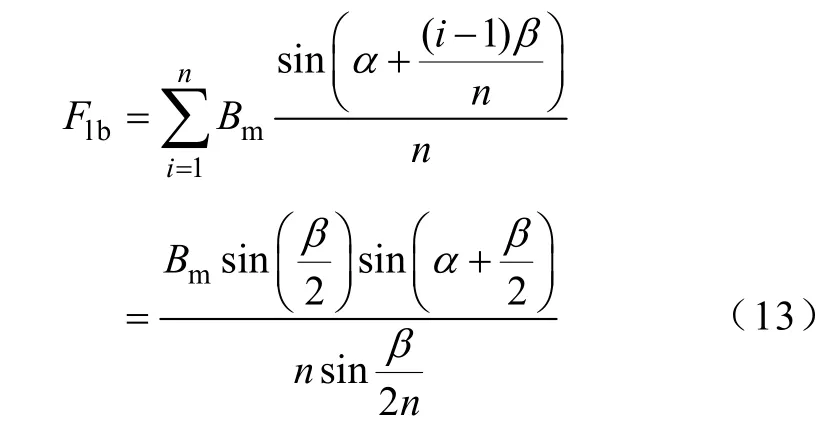
以误差ε考核两种不同分段方式下，计算精度随着的分段数的变化，其中，ε定义为

则根据式（7）、式（12）和式（13）可以得

由上述两式可发现，轴向分段的计算精度与位置α的选取无关。

分别取斜槽角度（电角度）为30°、60°、90°作为典型情况，比较ε1a和ε1b可以得到图3，图中横坐标为轴向分段数，纵坐标为不同分段数下的最大误差。由图3可知，分段方式2（见图2b）的收敛性能远远优于分段方式1（见图2a）。

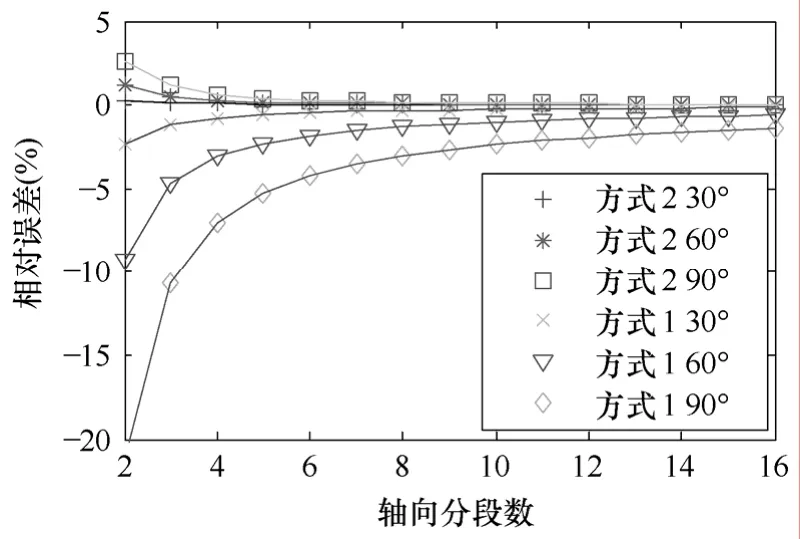
图3 两种分段方式收敛精度比较Fig.3 Convergence comparison of two slice methods

3.3 分段数对计算精度的影响

为分析斜槽分段数及斜槽角度对计算精度的影响，对气隙磁场基波、3次、5次、7次谐波随分段数及斜槽角度（电角度）分别取5°、15°、30°、45°、60°、90°变化的情况进行分析，这里轴向分段方式采用分段方式2。图4所示为导体在各次磁场中、不同斜槽角度情况下，分段数对其计算精度影响的分析结果。

分析图中曲线，可以得到如下结论：

（1）当电机斜槽角度较小时，可以取较小的轴向分段数；当斜槽角度增加时，轴向分段数需增加。

（2）一般情况下，利用有限元法分析电机的瞬态性能时，其斜槽分段数可以按照表1进行选择。

（3）同样的斜槽分段数，高次谐波磁场计算精度要低于基波及低次谐波磁场结果，但高次谐波相对数值较小，因此其对性能计算产生误差影响较小。

图4 分段数对计算精度影响Fig.4 Convergence comparison of slice number

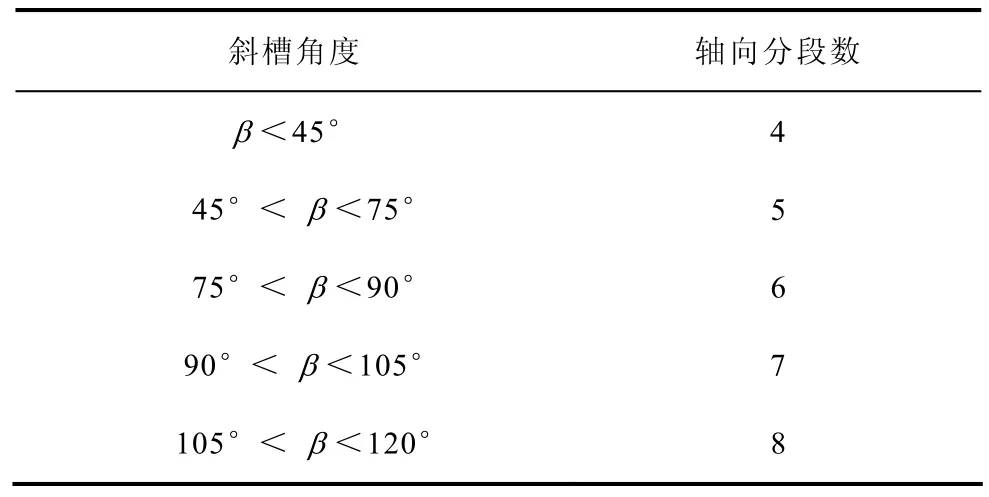
表1 轴向分段数选择Tab.1 Selection of slice number

3.4 考虑齿槽效应时的分段数分析

在上述分析中，忽略了开槽对电机磁场的影响，实际上，开槽后电机的反电动势和电磁转矩的瞬时值都将发生变化。

由于开槽，气隙磁场波形中将叠加齿谐波，该齿谐波将在三相绕组中感应齿谐波反电动势；对于异步电机，该齿谐波磁场将引起附加转矩。显然，它们对计算性能的影响与普通的谐波磁场的影响一致，因此这里不再重复讨论。

开槽对永磁同步电机转矩的影响，主要是齿槽转矩，假设齿槽转矩沿圆周一周的周期数为Nc，并设定齿槽转矩为正弦波变化，则可以推导得到

根据式（17），进行齿槽转矩分析时，轴向分段数需满足下式

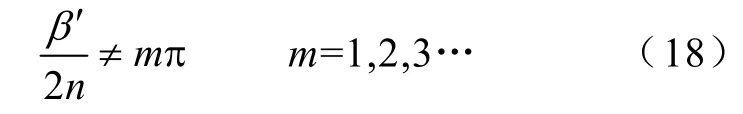
一般情况下，为了有效消除齿槽转矩，电机斜槽角度取为齿槽转矩周期的整数倍，即β′=2kπ，代入式（18），得到

事实上，为了精确分析齿槽转矩，通常分段数取得相对较多，一般首先满足n＞k，在此基础上，根据式（17）针对斜槽角度为齿槽转矩的1倍、2倍、3倍等情况进行分析比较，得到齿槽转矩计算精度与分段数的关系曲线如图5所示。

通常情况下，齿槽转矩计算其轴向分段数可按表2进行选择。

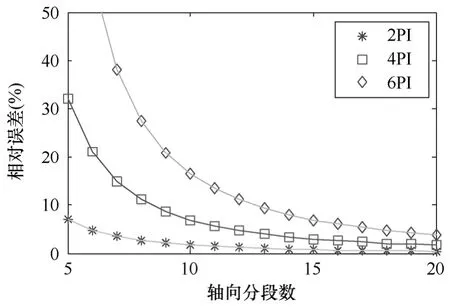
图5 分段数对齿槽转矩计算精度影响Fig.5 Cogging torque convergence comparison of slice number

表2 齿槽转矩轴向分段数选择Tab.2 Slice number selection for cogging torque caculation

4 软件仿真验证

为了验证前述关于分段方式、分段数解析分析的结论，本文利用EasiMotor有限元仿真进行验证，同时，本文采用了Flux软件对电机直轴和斜槽情况分别进行仿真比较，验证EasiMotor斜槽分析的正确性。

4.1 EasiMotor电机模型

在EasiMotor软件中建立某无齿曳引电机模型，模型参数见表3。

表3 电机基本参数Tab.3 The parameters of hoisting motor

图6所示为该曳引电机在EasiMotor软件中自动生成的结构模型和网格剖分模型，该电机采用32极72槽结构，轴向斜槽数为1个定子齿距。

图6 曳引电机二维有限元模型Fig.6 The 2D FEM model of motor

4.2 分段的有限元验证

在第2节的分析中， 忽略了齿槽以及各次谐波的因素，为了综合考虑以上因素，利用有限元法对两种分段方式以及分段数对计算精度的影响进行验证，分析采用EasiMotor软件，电机模型如图6所示，分析结果如图7所示，显然有限元分析结果与解析分析结果一致性良好。

图7 两种分段方式有限元比较Fig.7 FEM results comparison of two slice methods

4.3 有限元仿真比较

为对EasiMotor斜槽计算正确性进行验证，在EasiMotor 2.5与Flux 10.3中分别建立直槽/斜槽模型，验证EasiMotor计算的正确性。图8所示为电机采用直槽结构，在EasiMotor 2.5与Flux10.3软件中，对电机空载反电动势进行仿真结果比较，两者曲线几乎一致吻合。

图8 EasiMotor与Flux直槽仿真比较Fig.8 Simulation comparison between EasiMotor and Flux for linear model

当电机斜过一个齿距时，分别采用EasiMotor分段斜槽方法和Flux3D进行仿真，根据前述，在EasiMotor中轴向分段数采用6段，仿真结果如图9所示。由图9比较可见，EasiMotor软件采用分段斜槽方法进行电机斜槽分析时，计算结果与三维有限元分析结果高度吻合。

图9 EasiMotor与Flux斜槽仿真比较Fig.9 Simulation comparison between EasiMotor and flux for skew model

5 实验结果

基于EasiMotor仿真分析结果，本文进一步进行实物样机的测试分析，图10所示为电机空载反电动势（线电压）测试结果。

在图10中，比较实测数据与EasiMotor有限元分析结果（分段数取6），发现两者可以得到几乎完全相吻合的结果，该实验结果证明了EasiMotor基于分段斜槽技术的斜槽特性分析的正确性。

图10 测试结果与EasiMotor仿真结果比较Fig.10 Comparison between EasiMotor simulation and test

6 结论

斜槽对电机电磁性能有很大影响，因此在电机设计分析过程中，需要重点关注斜槽因素。EasiMotor在二维有限元中，采用分段斜槽的方法对斜槽电机进行分析，相较于三维有限元分析，可以大量节省计算资源，同时，在合理选择分段方式和分段数后，分段斜槽技术完全可以满足工程应用、科学研究的精度要求。

[1] 江建中，傅伟农，斜槽异步电动机的多截面有限元法分析[J].电工技术学报，1997，12(10)：1-7.Jian Jianzhong,Fu Weinong.Multi-slice finite element analysis of skewed induction motors[J].Transactions of China Electrotechnical Society,1997，12(10)：1-7.

[2] 胡敏强，黄学良.电机运行性能数值计算方法及其应用[M].南京: 东南大学出版社，2003.

[3] Joao Bastos,Nelson Sadowski,Marcel Dekker.Electromagnetic modeling by finite element methords[M].New York: Marcel Oekker,Inc,2003.

[4] Jin Jianming.The finite element method in electromagnetics[M].New York: John Wiley& Sonc,Inc.,2002.