基于改进型遗传算法的舰艇航路规划研究*
田 鹤 李启华 孟一鸣
(海军兵种指挥学院 广州 510430)
1 引言
航线设计问题本质上是航路任务规划问题。航路规划是在特定约束条件下寻找运动体从初始点到目标点并且满足某种性能指标最优的运动轨迹[1]。对于一个优化问题,如果其目标函数是可微的,并且问题的规模不是很大,我们可以采用一些传统的优化方法解决,如可视图法、人工势场法等,可是对于目标函数不可微甚至不连续,或者虽然目标函数可微但问题的规模非常大的优化问题,很多传统的优化方法往往不再适用[2]。由于遗传算法不要求目标函数的可微及连续性,而且可以在容许的时间范围内找到大规模优化问题的满意解,因此,近年来,遗传算法已成为路径规划中使用较多的一种方法。
该方法被广泛应用于舰艇、飞行器和机器人的航路规划中,但是考虑到基本的遗传算法存在搜索时间长,初始种群生成质量差等问题,本文对其进行改进,即采用蚁群算法的搜索策略生成航线的初始种群,然后用遗传算子对其进行遗传操作,进而搜索出最优航线,仿真结果表明,改进后的遗传算法在航路的搜索效率、初始种群的生成质量、及最优航线的选择上有了明显的提高。
2 遗传算法用于航路规划
2.1 初始群体的产生方法
初始种群是遗传算法迭代运算的起点,它由一定数目的个体所组成,当网格数目较多时产生初始种群并非易事。由于遗传算法的初始种群生成没有统一的模式,因此考虑采用蚁群的搜索策略生成航线初始种群。采用蚁群算法的前行搜索遵循以下三条规则:
1)前行网格点必须是可行点;
2)搜索时避开已选择的网格点;
3)搜索时如果下一网格点均不满足上述两条件,则删除该点,从上一点开始重新选择。
经过蚁群搜索后生成的两条初始航线如图1所示。
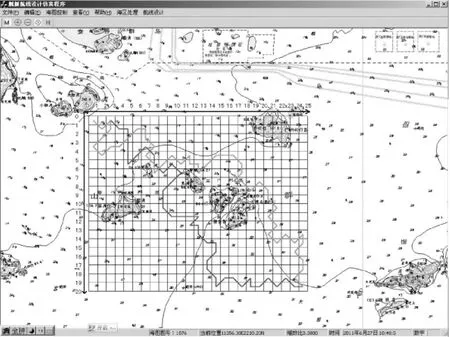
图1 初始航线生成示意图

图2 网格编码示意图
2.2 种群的编码方法
由于采用蚁群算法的搜索策略生成航线的初始种群,因此种群的编码方法既要适用于蚁群算法的单步搜索,又要方便遗传算子对其进行操作,基于此考虑采用变长网格序号的方法进行编码。在采用网格序号进行编码时首先要对任务海区进行网格离散化。离散具体方法可参考相关文章[7],在此不做详细介绍。序号法比直角坐标表示网格点简洁,同时在操作过程中可以将网格的序号和直角坐标关联起来,由于直角坐标更便于表示网格之间的相对位置,因此在对航线进行适应度评价时可以利用网格对应的直角坐标计算航线的航程及检验航线的可行性。图中直角坐标和网格的转换关系为[3]:

式中N表示蚂蚁搜索过程中经过的网格点的序号,x,y表示对应的直角坐标,其中,mod表示取余操作,int表示取整操作。图1所示航线如果用序号编码表示为:(0,1,7,12,17,18,24),用直角坐标表示形式为:((0,0),(1,0),(2,1),(2,2),(2,3),(3,3),(4,4))。由此可见采用网格序号编码较直角坐标编码具有编码长度短、简明、直观的优点。编码过程中网格点的数据结构为:
struct GridNode//每个节点的数据结构包括该节点x,y坐标该节点的编号o
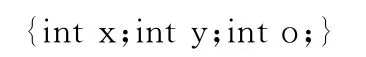
航线个体的数据结构表示为:struct antindividual{
double value;//目标值
double fitness;//适应度值
int grid_n;//对应的航线网格节点数
struct GridNode node[100];//网格节点数组 }
2.3 适应度函数的建立
个体的适应度函数直接影响到遗传算法的计算效率[4]。一般在用遗传算法解决某一优化问题时,首先针对该问题进行目标函数的构建,然后再由目标函数转化为适应度函数。舰艇航路规划时主要考虑三方面因素:即安全性、隐蔽性、及时性[5~6]。针对上述三个因素,在进行航路规划时主要从威胁代价、航程代价两个方面进行目标函数的构建。
2.3.1 航程代价函数模型
舰艇航线的航程为航路上各转向节点(各网格点)之间的距离之和。以Dcost表示航程代价,则其表达式为:

式中N为航路段数,n为网格节点数,li为第i航路段的长度,x,y分别为航路段中网格节点所对应的直角坐标。
2.3.2 威胁代价函数模型
威胁代价模型包括威胁概率模型和威胁函数模型[7]。
1)各种威胁概率模型
(1)水深威胁概率模型。水深威胁主要指可能不满足舰艇吃水的浅水区域。以浅水区域中心为圆心,以覆盖浅水区域的距离R为半径画圆,令舰艇距圆心的距离为d,建立其威胁概率函数模型
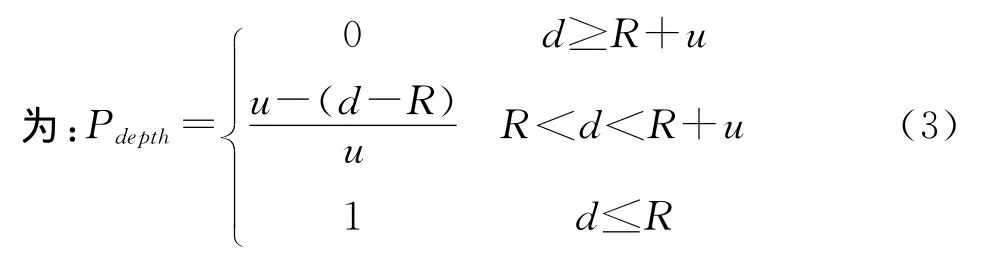
上式中,u为水深安全系数修正值,为一固定值,且u>0。
(2)障碍物威胁概率模型。障碍物威胁区域可以用一圆形区域近似表示。设R是影响区域的最大半径,d是舰艇到障碍物区域中心的距离,建立其威胁概率函数模型为:

上式中γ为障碍物安全系数修正值,为一固定值,且γ>0。
(3)军事威胁概率模型。军事威胁一般为敌火炮、导弹等火力威胁,其威胁区域一般为敌武器系统的有效杀伤区域,基本上是以火力发射点为圆心,武器射程为半径的圆。设武器系统的最大杀伤范围为R,舰艇到威胁区域中心的距离为d,建立其威胁概率函数模型为:

上述三个模型的威胁概率值在距离最大处为0,在距离最小处为1,且威胁概率模型具有连续性,满足距离越小,威胁程度越大的原则,可以较好地描述威胁源随距离变化的威胁概率分布情况,在进行航路规划时,可以针对不同的任务情况特点,对不同的威胁赋予不同的权重系数。
2)威胁代价函数模型
由于一整条航线是由各个网格节点之间的航路线段组成的,因此可以将整条航线的威胁代价转为对每个网格点的威胁代价的累加。根据这一思想,建立威胁代价函数模型为:
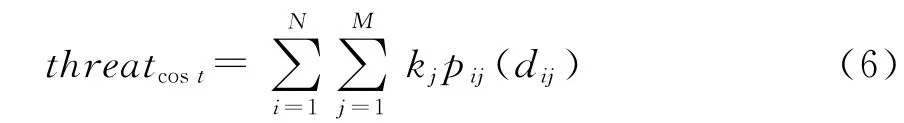
上式中N为网格节点数,M为威胁源数目,pij(dij)为j威胁源对网格点i的威胁概率,dij表示网格点i到威胁源j的最近距离,kj为威胁源j的权重系数。
2.3.3 目标函数模型
建立了航程代价函数模型和威胁代价函数模型后,可综合建立航线的目标代价函数为:
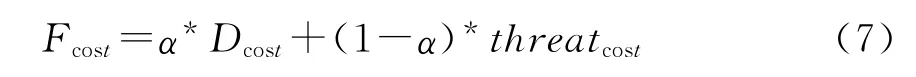
代入各自的计算公式为:
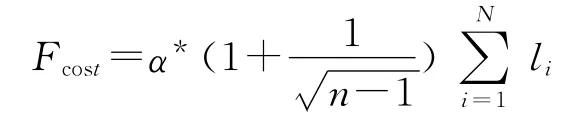
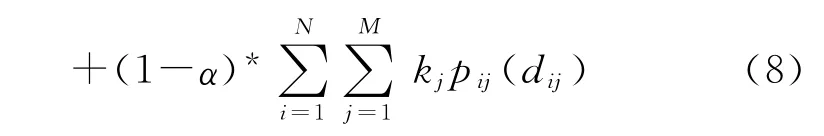
2.3.4 适应度函数模型
航线代价函数与适应度函数的转化结合遗传算法对适应度函数的约束条件,可以采用以下形式来实现航线目标代价函数与航线适应度函数之间的转换[8]:

上式中,β为一系数修正值,Cmin为一正的固定值。经过上式的转换,即将代价函数的最小值问题转换为求适应度函数的最大值问题,完全符合遗传算法对适应度值的求解约束条件。
2.4 遗传算子的设计
2.4.1 选择算子
采用比例选择算子,使个体按照与适应度成正比的概率向下一代群体繁殖。具体方法为计算出每一个个体的适应度值,然后计算该适应度值占所有个体适应度值的比例大小,比例大的被选中的概率高,比例低的被选中的概率小,经过N次循环,就得到N个适应度值相对比较高的航线个体。
2.4.2 交叉算子
采用重合点单点交叉的方法。具体方法为随机选出两条航线,从起始节点开始查找两条航线的重合点(即网格序号相同点),然后对其进行标记,查找完毕后,任意选择其中一个交叉点进行交叉,即将该点之后的两条航线部分互换。采用这种交叉方式优点是便于操作,而且可以保证交叉后的两条航线也是可行的。
2.4.3 变异算子
考虑采用插入和删除的方法。插入操作的具体方法为:随机选择一条航线个体的网格节点,然后将网格节点周围最近的一个可行网格点插入航线个体,比较新生成航线个体和未插入节点之前的航线个体的适应度值大小,若适应度值提高,则用新航线个体替代以前航线个体,若不提高或降低,则选择以前航线个体。删除操作的具体办法为:查找航线个体中有没有相同序号的网格节点,若有则将两相同序号之间的冗余序号,连同两相同节点中的一个一并去掉,得到一条网格节点变少,适应度值提高的新航线个体。
2.5 终止条件的设定
遗传操作在进行跌代时的终止遵循以下规则:
1)强制终止。即设定最大进化代数T,当超过最大进化代数时,迭代操作强制终止。
2)条件终止。即如果种群在进化过程中每一代的最优个体的适应度值趋于一恒定值时,迭代终止。条件终止的公式为:
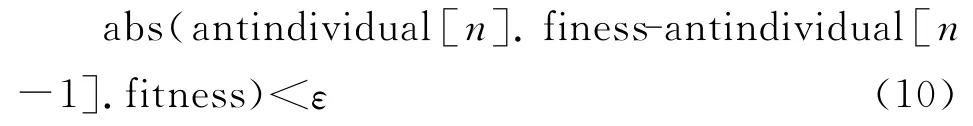
ε为一固定值。abs()为取绝对值函数。
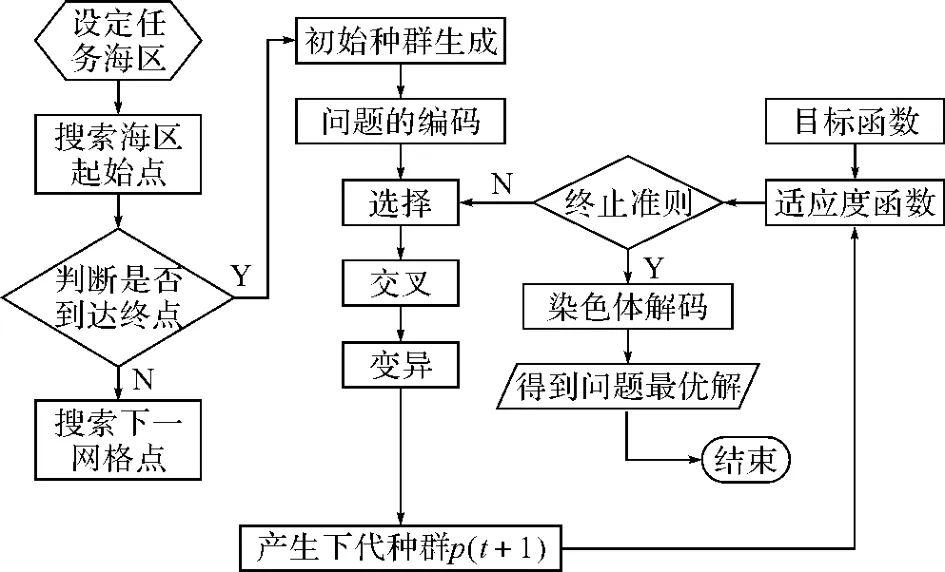
图3 仿真实现流程图
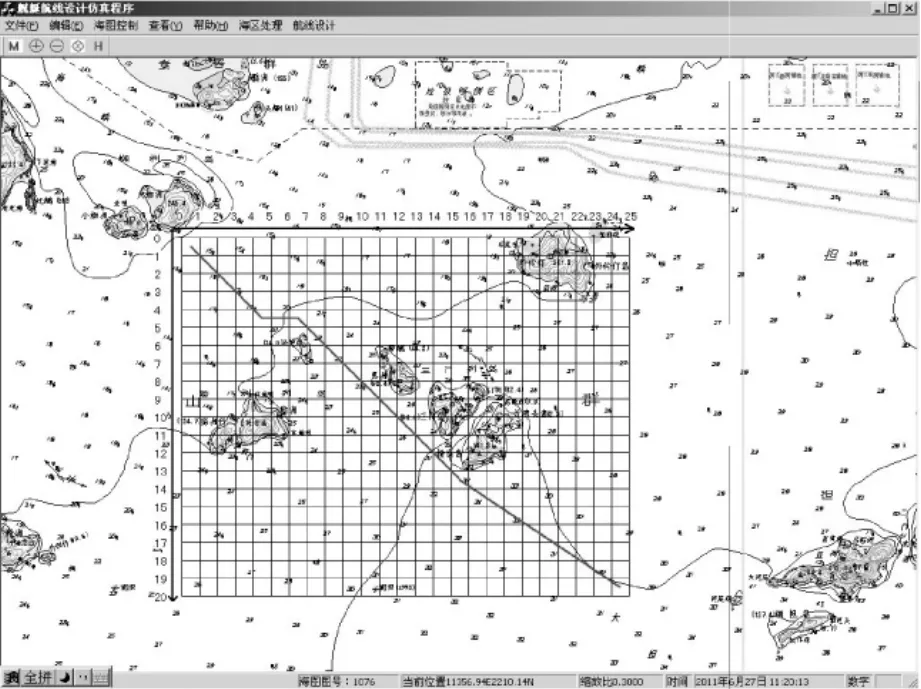
图4 仿真验证示意图
3 仿真实现
利用遗传算法进行航路规划的编程仿真实现,编程时采用流程图如图4所示,根据流程图所示过程,采用 VC++6.0进行编程实现[9,12],遗传参数分别为{M,T,Pc,Pm}={20,100,0.6,0.01},仿真实现后的最优航线如图所示。
4 结语
通过仿真试验证明,采用简化的蚁群方法生成初始航线种群时,可以保证航线初始种群的可行性,提高了遗传操作的效率,而且采用网格点序号的编码方法,编码方法简单,易于对其进行遗传操作,经过一定代数的操作之后即可以得到满足条件的航线。
[1]刘环宇,董受全.简约航路规划方法[J].火力与指挥控制,2008,33(7):61~63
[2]巩敦卫,孙晓燕.协同进化遗传算法理论及应用[M].北京:科学出版社,2009:1~3
[3]王莹,刘维亭.基于改进蚁群算法的舰船航路规划研究[J].现代电子技术,2010,21(5):186~196
[4]周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999:157~159
[5]张高.基于蚁群算法的舰艇航线设计问题研究[D].广州:海军兵种指挥学院,2009:34~36
[6]杜新海,等.航海学[M].广州:海潮出版社,1995:38~39
[7]汲万峰,姜礼平,朱建冲.基于遗传算法的航路规划模型研究[J].军事运筹与系统工程,2010,24(2):52~55
[8]汤先拓.基于遗传算法的舰艇航线自动生成研究[J].广州:海军兵种指挥学院,2009:41~42
[9]孙鑫,余安萍.VC++深入详解[M].北京:电子工业出版社,2009:49~56
[10]熊瑜,饶跃东.基于改进蚁群算法的无人飞行器航迹规划[J].计算机与数字工程,2010,38(7)
[11]宋久元,滕国库,胡丽霞.路径规划算法的改进及在车载导航中的应用[J].计算机与数字工程,2010,38(8)
[12]张岳新.VisualC++程序设计[M].苏州:苏州大学出版社,2002:102~104

