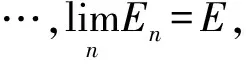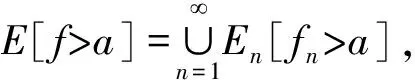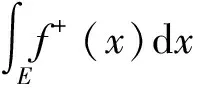希尔伯特空间上的L测度和L积分
郑利凯
(内蒙古民族大学 数学学院,内蒙古 通辽 028000)
我们知道n维欧氏空间Rn上的Lébesque测度和Lébesque积分[1-2]是现代数学的基础,那么Lébesque测度和Lébesque积分是否可以推广到抽象的函数空间上呢? 这是现代数学需要研究的课题.许多文献对这一问题进行了深入研究[3-5].下面将Rn上的Lébesque测度和Lébesque积分推广到Hilbert空间上,给出Hilbert空间上Lébesque测度和Lébesque积分的定义.
1 Hilbert空间上的Lébesque测度
首先,若Hilbert空间X为零空间,即X={0},则X的Hilbert维数为0.那么定义X的Lébesque测度为0,即mX=0.
若X为非零有限维Hilbert空间,则X必有完全规范正交系.设X的完全规范正交系的基数即Hilbert维数为n,则n≠0.下面证明,X与n维欧氏空间Rn同构.即存在由Hilbert空间X到n维欧氏空间Rn的映射T,使得∀x,y∈X及数α,β,满足:
T(αx+βy)=αT(x)+βT(y),
其中
引理1n维Hilbert空间X和n维欧氏空间Rn同构.
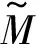

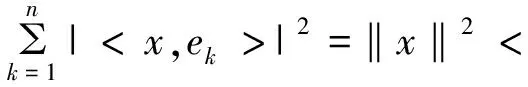
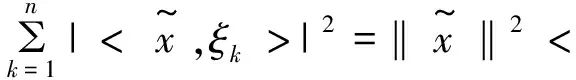
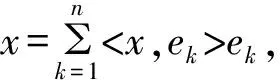
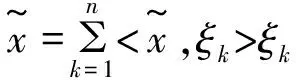
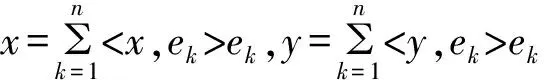
所以T是X到Rn上的同构映射.
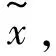

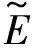
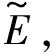
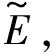
根据Rn中勒贝格测度的知识,可以得到以下结论:
定理1 Hilbert空间X中凡是具有正测度的集必含有不可测子集.
2 Hilbert空间上的Lébesque积分
下面将n维欧氏空间Rn上的Lébesque积分推广到n维Hilbert空间X上.
2.1 Hilbert空间上的Lébesque可测函数
定义3 设f(x)为定义在n维Hilbert空间X上的实函数,如果对于任何有限实数a,E[f>a]都是可测集,则称f(x)为定义在X上的Lebesgue可测函数,或称f(x)可测, 其中E[f>a]={x|x∈X,f(x)>a}.
根据Rn中勒贝格测度的知识,可以得到以下结论:
定理2 设f(x)是定义在n维Hilbert空间X中可测集E上的实函数,下列任一条件都是f(x)在E上可测的充要条件:
(i)对任何有限实数a,E[f≥a]都可测;
(ii)对任何有限实数a,E[f (iii)对任何有限实数a,E[f≤a]都可测; (iii)对任何有限实数a,b(a 定理3 (i)设f(x)是定义在n维Hilbert空间X中可测集E上的可测函数,而E1⊂E为E的可测子集,则f(x)看作定义在E1上的函数时,它是E1上的可测函数. 定理4 设f(x),g(x)是定义在n维Hilbert空间X中可测集E上的可测函数,则E[f>g]与E[f≥g]都是可测集. 定理5 设f(x),g(x)是定义在n维Hilbert空间X中可测集E上的可测函数,则下列函数(假定它们在E上有意义)在E上皆可测: (i)f(x)+g(x);(ii)|f(x)|;(iii)1/f(x);(iv)f(x)·g(x). 根据Rn中勒贝格积分的定义,容易得到下面的定理: (ii)设分划D′比D细,则s(D,f)≤s(D′,f),S(D,f)≥S(D′,f); (iii)对于任意两个分划D,D′,总有s(D,f)≤S(D′,f); 下面给出Hilbert空间中有界集上有界函数的Lébesque积分的定义. 定义6 设f(x)为n维Hilbert空间X中测度有限的可测集E上的有界函数,记: 分别称为f(x)在E上的上,下积分. 根据Rn中勒贝格积分的有关知识,容易得到下面的定理: 定理9 设f(x)是n维Hilbert空间X中测度有限的可测集E上的有界函数,则f(x)在E上Lebesgue可积的充要条件是:∀ε>0,∃E的分划D,使得: 这里ωi=Bi-bi. 定理10 设f(x)是n维Hilbert空间X中测度有限的可测集E上的有界函数,则f(x)在E上Lebesgue可积的充要条件是f(x)在E上可测. 首先,讨论定义在n维Hilbert空间X中的可测集E(不要求mE<)上的非负实函数f(x)的Lebesgue积分. 同时f(x)可用一列定义在En上而函数值随着n逐渐增大的有界函数fn(x)来逼近: 定义7 设f(x)为n维Hilbert空间X中的可测集E上的非负可测函数,定义: 为f(x)在E上的Lebesgue积分. 下面,讨论定义在n维Hilbert空间X中的可测集E(不要求mE<)上的一般实函数f(x)(不要求f(x)≥0)的Lebesgue积分. 令f+(x)=max{f(x),0},f-(x)=max{-f(x),0},则f(x)=f+(x)-f-(x).不难证明f(x)在E上可测等价于f+(x)与f-(x)在E上可测,且有: 为f(x)在E上的Lebesgue积分.特别当此积分有限时,称f(x)在E上Lebesgue可积. 这样就把Lébesque积分推广到Hilbert空间上,开辟了新的数学研究领域. 参考文献: [1]程其襄,张奠宙,魏国强,等.实变函数与泛函分析基础[M].2版.北京:高等教育出版社,2003:106-122. [2]周民强.实变函数论[M].北京:北京大学出版社,2001:171-182. [3]陈希孺.关于测度的一个收敛定理[J].数学进展,1965(1):90-97. [4]李梅.关于测度的扩张及其完备化[J].南华大学学报:自然科学版,2003(1):65-68. [5]闫国军,宿金勇.Π类上测度的扩张[J].郑州大学学报:自然科学版,1998(2):21-24.
2.2 Hilbert空间中有界集上有界函数的Lébesque积分
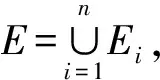
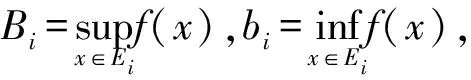

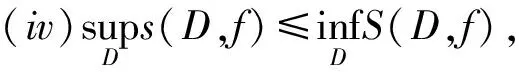
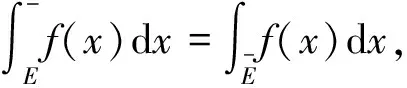
2.3 Hilbert空间中无界集上一般实函数的Lébesque积分