负二项分布可靠度的E-Bayes估计
苏清华,胡中波
(1. 孝感学院 数学与统计学院,湖北 孝感 432000;2. 武汉理工大学 理学院,湖北 武汉 430074)
在生产、生活中人们对产品的可靠性要求越来越高,如果用成败型实验对产品进行可靠性测试,那么产品寿命是以成败次数来衡量的. 负二项分布就是此类测试产品寿命服从的分布之一.
在高可靠性产品的重复独立抽样检验中,θ(0<θ<1)为每次抽到合格品的概率,当第r个合格品出现时终止试验.X为第r个合格品出现之前不合格品的个数,则X服从参数为r和θ的负二项分布,其分布律为:
(1)
其中:r>0已知,θ为产品的可靠度(或合格品率、成功率).
目前已有不少文献探讨了求负二项分布可靠度的Bayes估计、经验Bayes估计和多层Bayes估计的方法,但几乎都是在平方损失的情况下进行讨论. 而E-Bayes估计可以看作是对多层Bayes估计的修正,自E-Bayes估计法提出以来[1],主要研究的是几何分布、二项分布和Pascal分布可靠度的估计[2-4],以及失效概率和状态概率的估计[5-6].本文作者在文献[7]中给出了熵损失函数下,先验分布为幂分布时,负二项分布可靠度的E-Bayes和多层Bayes估计. 本文则进一步在熵损失函数下,给出了当负二项分布可靠度的先验分布为Beta分布时,可靠度的Bayes估计、E-Bayes估计及多层Bayes估计,并通过数值试验讨论先验分布为幂分布时,负二项分布可靠度的E-Bayes估计和多层Bayes估计的优越性.
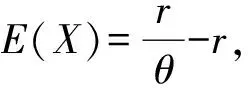
(2)
其中δ是θ的估计,且L(θ,δ)关于δ是严凸的.
给定负二项分布(1)中可靠度θ的先验分布为Beta分布,其密度为:
(3)
其中:a>0,b>0,0<θ<1.当b=1时,Beta分布即为幂分布,其密度为:π(θ|a)=aθa-1.
1 可靠度的Bayes估计
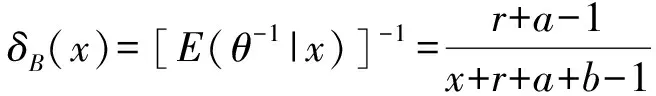
证明令δ(x)是θ的任一估计,在熵损失函数(2)下,δ(x)的Bayes风险为:
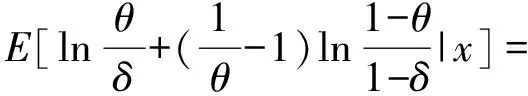
(4)
对上式关于δ求导并令其等于零,可得:δ=[E(θ-1|x)]-1,且当δ→1或0时后验风险趋于+,从而δ=[E(θ-1|x)]-1即为使后验风险最小的估计,故对于任何先验分布在熵损失函数(2)下,负二项分布可靠度θ的唯一Bayes估计为:δB(x)=[E(θ-1|x)]-1.
给定θ的先验分布为Beta分布(3),则根据Bayes定理,θ的后验密度函数为:
于是,在熵损失函数(2)下,先验分布为Beta分布(3)时,θ的唯一Bayes估计为:
令b=1,即可得可靠度的先验分布为幂分布时,负二项分布(1)的可靠度θ的唯一Bayes估计为:
2 可靠度的E-Bayes估计
由模型(1)在高可靠度成败型试验中获得的样本数据大部分包含的次品数极少,一般X=0,1,2,因此可靠度θ较大的可能性大,而较小的可能性小. 根据构造多层先验分布的增函数法[8],应选取θ的增函数作为θ的先验分布的密度函数的核,因此Beta分布(3)中应选择a>1,0 定理2 对负二项分布(1),在熵损失函数(2)下: 1)若可靠度θ的先验分布为Beta分布(3),且取a,b在θ上的先验分布分别为:π(a)=U(1,c),π(b)=U(0,1),其中:c为待定参数,则θ的E-Bayes估计为: (x+1)(x+r+c)[ln(x+r+c)-1]+(x+1)(x+r+1)[ln(x+r+1)-1]- x(x+r+c-1)[ln(x+r+c-1)-1]-x(x+r)[ln(x+r)-1]}; (x+1)(x+r+c)[ln(x+r+c)-1]+(x+1)(x+r+1)[ln(x+r+1)-1]- x(x+r+c-1)[ln(x+r+c-1)-1]-x(x+r)[ln(x+r)-1]}; E-Bayes估计是对多层Bayes估计的一种修正,以下给出θ的多层Bayes估计,以便与θ的E-Bayes估计进行比较. 定理3 对负二项分布(1),在熵损失函数(2)下: 1)若可靠度θ的先验分布为Beta分布(3),且取a,b在θ上的先验分布分别为π(a)=U(1,c),π(b)=U(0,1),其中c为待定参数,则θ的多层Bayes估计为: 2)若可靠度θ的先验分布为幂分布,且取a在θ上的先验分布分别为π(a)=U(1,c),其中c为待定参数,则θ的多层Bayes估计为: 证明θ的多层先验密度为: 则θ的后验密度为: 从而θ在熵损失函数(2)下的多层Bayes估计为: 表和δ-的计算结果 本文给出了熵损失函数下,当可靠度的先验分布为Beta分布和幂分布时,负二项分布可靠度θ的Bayes估计、E-Bayes估计及多层Bayes估计.首先,由定理2和定理3中所得结果可见,E-Bayes估计公式不涉及积分,计算更简单;其次,数值试验结果表明,先验分布为幂分布时可靠度的E-Bayes估计和多层Bayes估计相差较小,精度都较高,但E-Bayes估计稳健性更高.因此,E-Bayes估计作为对多层Bayes估计的修正方法,更优越,更便于在实际中应用. 参考文献: [1]HanMing,DingYuan-yao.SythesizedexpectedBayesianmethodofparametericestimate[J].JournalofSystemsScienceandSystemsEngineering,2004,13(1):98-111. [2]韩明.Pascal分布的参数估计[J].纯粹数学与应用数学,2006,22(4):510-515. [3]韩明.产品可靠度的E-Bayes估计[J].大学数学,2007,23(3):83-87. [4]熊常伟,张德然,张怡,等. 几何分布可靠度的Bayse估计[J].统计与决策,2007,20(2):21-22. [5]MingHan.E-Bayesianestimationoffailureprobabilityanditsapplication[J].MathematicalandComputerModeling,2007,45( 9/10 ):1272-1279. [6]韩明.状态概率的E-Bayes估计与多层Bayes估计[J]. 运筹与管理,2006,15(5):70-74. [7]苏清华,刘次华.熵损失下负二项分布可靠度的E-Bayes估计[J].湖北师范学院学报:自然科学版,2009,29(3):14-17. [8]韩明.多层先验分布的构造及其应用[J]. 运筹与管理,1997,6(3):31-40.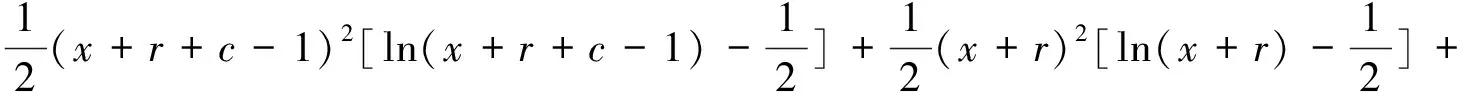
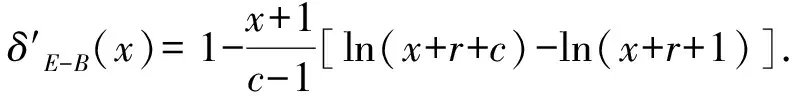
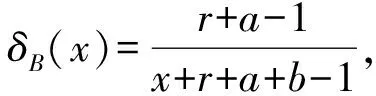
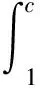
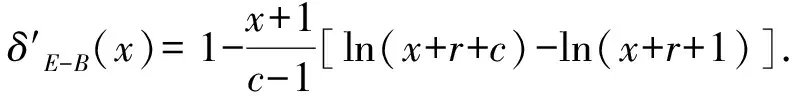
3 可靠度的多层Bayes估计


4 数值试验
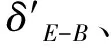
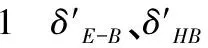
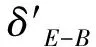
5 结束语

