BC毛虫树的BC子树数

2011-06-05 06:41惠志昊

杨雨，惠志昊

(1.平顶山学院国际教育交流学院,河南平顶山 467000；2.平顶山学院数学与信息科学学院,河南平顶山 467000)

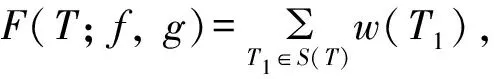
如果树T有一条路径，使得T的每个顶点如果不在该路径上，则一定与路径上的某个顶点相邻，则称此树为毛虫树；若T同时又是一棵BC树，则称T为一棵BC毛虫树，本文给出了BC毛虫树的概念，并用生成函数的方法来研究毛虫BC树的BC子树数及它的特殊性质.

1 BC毛虫树的BC子树数

定理1[3]n顶点星形BC树K1,n-1有2n-1-n个BC子树,比任一个n顶点BC树所含的BC子树都多；路径BC树Pn有(n-1)2/4个BC子树, 比任一个n顶点BC树所含的BC子树都少.

定理2[3]星形BC树K1,n-1中含顶点vi(i=1,2,…,n-1)的BC子树的个数为2n-2-1.

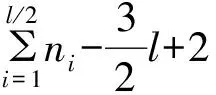
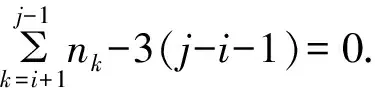
图1 直径长度为l的BC毛虫树T′

证明用归纳假设证明,l=2时BC毛虫树即为星形BC树，由定理1知其成立.

假定对于直径为l-2的BC毛虫树T是成立的,

即:

(1)

直径长度为l的BC毛虫树T′, 由BC毛虫树的特点可知,T′的BC子树由四部分构成.

1)T的所有BC子树；

2)K1,nl/2-1的所有BC子树；

3)T中的含顶点v的BC子树与K1,nl/2-1的含顶点v的BC子树相结合生成的BC子树；

4)T的含顶点v的奇长路径子树与K1,nl/2-1的边(v,w)合并形成的BC子树, 经计算此种类型的有(l-2)/2个.

即η(T′)=η(T)+η(K1,nl/2-1)+η(T,v)×η(K1,nl/2-1,v)+(l-2)/2

由定理1和2可知:η(K1,nl/2-1)=2nl/2-1-nl/2，η(K1,nl/2-1,v)=2nl/2-2-1.

分析BC毛虫树的性质，BC毛虫树T的含顶点v的BC子树的个数为:

η(T,v)=(2nl/2-1-2-1)+2nl/2-1-3×(2nl/2-2-2-1)+2nl/2-1-3×2nl/2-2-3(2nl/2-3-2-1)+

结合式(1)可得:

(l-2)(l-4)/8+(2nl/2-1-nl/2)+(2nl/2-2-1)[(2nl/2-1-2-1)+

2nl/2-1-3×(2nl/2-2-2-1)+2nl/2-1-3×2nl/2-2-3(2nl/2-3-2-1)+

…+2nl/2-1-3×2nl/2-2-3×2nl/2-3-3…2n2-3(2n1-2-1)]+(l-2)/2=

定理得证.

定理4BC毛虫树T′同上, 叶子数按照区域进行划分，从左到右依次是X1,X2,…,Xl/2, 将前i部分的叶子全部移到X1之后, 所产生的BC毛虫树记为T″, 则直径长度:

证明记由树T′变换成T″后各部分的顶点数目为：

因此：

故:

(2)

式(2)小于等于0等价于:

即:

(3)

式(3)成立时η(T″)≤η(T′), 定理得证.

由于BC树性质比较特殊，国外有很多相关的研究[1，4-5]，同时毛虫树的相关研究也很多[7-8]，本文结合毛虫树和BC树的特性，给出了BC毛虫树的概念，并对它的BC子树数进行了计算，同时给出了它的一个特殊性质.

参考文献:

[1]Harary F,Plummer M D.On the core of a graph[J].Proc London Math Soc,1967,17:305-314.

[2]Yan W,Yeh Y-N.Enumeration of subtrees of trees[J].Theoretical Computer Science,2006,369:256-268.

[3]杨雨，王德强.两类BC树的BC树的计数[J].大连海事大学学报,2007,S1:62-65.

[4]Harary F,Prins G.The block-cutpoint-tree of a graph[J].Publ Math Debrecen,1966,13:103-107.

[5]Mkrtchyan V V.On trees with a maximum proper partial 0-1 coloring containing a maximum Matching[J]. Discrete Mathematics,2006,306: 456-459.

[6]Frank Harary, Allen J Schwenk.The number of caterpillars[J].Discrete Mathematics,1973,6(4):359-365.

[7]Slobodan K Simica, Enzo Maria Li Marzib, Belardob F.On the index of caterpillars[J].Discrete Mathematics,2008,308:324-330.

[8]卞瑞玲.毛虫树的性质[J].山东大学学报:理学版,2002,37(6):504-507.