舰机协同防空作战信息网络的复杂性分析与实证
徐圣良,姜青山,单利建
(1.海军兵种指挥学院,广州 510430;2.海军航空工程学院,山东 烟台 264001;3.中国人民解放军91561部队,广州 510320)
0 引言
航母编队防空是急待研究的新课题,在航母编队防空作战中,舰艇与飞机的协同作战能够极大地提高防空作战效能[1],因此舰机协同防空作战理论作为一种提高航母编队防空作战效能的新方法被提出来[2]。关于防空作战效能的评估,前人一般采用ADC效能评估、模糊综合评判等方法,采用这些方法建立的模型存在参数不确定的缺点。在航母编队防空作战中,以信息为纽带将分布在不同阵位的舰艇、飞机等各种作战平台联结成一个复杂的作战网络,使得作战进程呈现出典型的复杂网络特征,采用复杂网络理论的研究方法建立的模型具有更贴近实际的优势。因此,本文试图利用近几年来发展起来的网络复杂性理论,对舰机协同作战系统的信息网络模型和特征进行研究,这是研究航母编队防空作战的一种新方法,具有创新意义。
1 航母编队舰机协同信息网络结构
1.1 指挥控制网络结构分析
航母编队是海上合成编队,其内部指挥关系非常复杂。按扁平化指挥原则,航母编队在编队内设置编队指挥所(设在航母)、航母本舰指挥所(设在航母)、舰艇群指挥所(护航舰艇组成的区域防空群,群指挥所开设在装备海上编队作战指挥系统的舰艇)。
1.2 航母编队指挥控制网络中信息的分类
航母编队指挥控制网络的信息按照战术用途可分为情报类信息、指挥控制类信息和保障类信息。
2 基于复杂网络的航母编队防空作战舰机信息协同
2.1 平台中心防空作战模式与舰机协同防空作战模式的信息协同比较
2.1.1 平台中心防空作战信息协同建模及分析
平台中心防空作战模式下的信息协同模型如图1所示,平台中心防空作战各个作战平台之间仅仅依靠战场感知节点连接,即两个平台之间通过传感器建立通信联系。以平台为中心的防空作战,信息传输是烟囱式的树状结构,信息不能快速共享[3]。

图1 平台中心防空作战:独立职责Fig.1 Platform-centric air defense operation:divided duties
2.1.2 舰机协同防空作战信息协同建模及分析
舰机协同防空作战模式下的信息协同模型如图2所示。
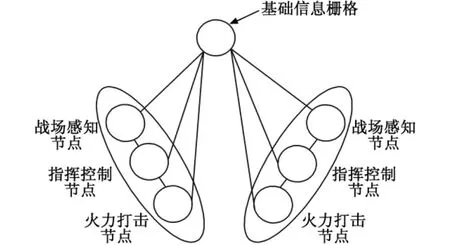
图2 舰机协同防空作战:信息协同Fig.2 Warship-aircraft cooperated air defense operation:information cooperation
与图1比较得出,舰机协同防空作战与平台中心防空作战在信息协同方面的区别在于作战平台之间的信息链接不同。平台中心防空作战各个作战平台之间仅仅依靠传感器节点连接,而舰机协同防空作战通过基础信息栅格来连接所有作战单元的战场感知节点、指挥控制节点和火力打击节点[4],信息传输是网状的结构,舰艇和飞机之间每个作战平台都能实时共享信息[5]。
2.2 基于复杂网络的舰机协同作战系统结构
与传统的平台中心防空作战模式不同,在舰机协同防空作战模式下,航母编队的作战系统更加强调信息互联、互通和互操作的重要性,进而形成综合所有作战资源的舰机协同作战系统。基础信息栅格将传感器网、指挥控制网、火力打击网的计算机组成一个大系统,实现编队内各分系统的协同。这一作战样式的变革带来了航母编队作战系统内部结构的变化,系统各组成单元以基础信息栅格为依托,以信息流为纽带,把编队的战场感知网络、指挥控制网络和火力打击网络的节点联结成了纵横交错的复杂网络结构,可以构建舰机协同防空作战系统的拓扑模型,如图3所示。
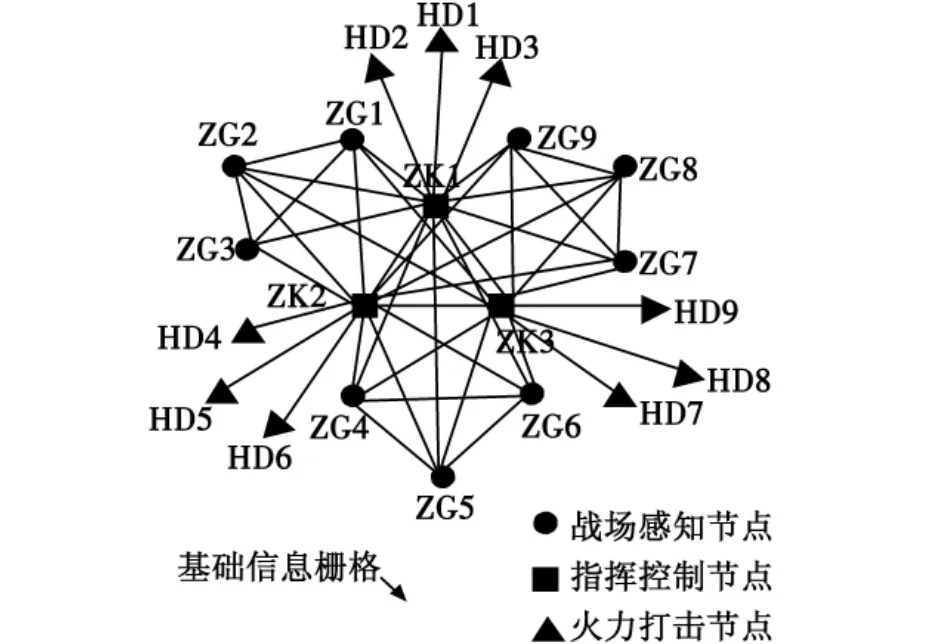
图3 舰机协同防空作战系统拓扑模型Fig.3 Topological model of warship-aircraft cooperatied air defense operation system
原则上说,任何包含大量单元(或元素)的复杂系统,当人们把构成单元抽象成“节点”,单元(或元素)之间的相互作用抽象为“边”时,都可以当作复杂网络来研究。图3中,各网格单元构成了网络模型的节点,单元之间的交互关系构成了节点之间的连接,因此航母编队防空作战系统可作为复杂网络研究。
3 基于复杂网络的航母编队作战系统信息网络的描述
3.1 网络特征评价参数
反映网络结构特征的参数有很多,最重要的有以下几点。
1)节点的度k。节点i的度ki是指节点i具有的连接边的数量,或者是指节点i的邻接节点的数量。在编队中是各种传感器、指挥控制台、通信设备和武器装备的邻接节点的数量。
2)节点的度分布P(k)。节点的度分布P(k)是指随机选择网络中任意一个节点,该节点的度恰好为k的概率,反映了网络拓扑的连接情况。在编队中是各种装备的度恰好为k的概率。
3)节点之间的距离dij。节点对(i,j)之间的距离dij是指连接节点i和节点j之间最短路径的边的数量。
4)平均路径长度L。网络的平均路径长度L定义为任意两个节点之间的距离的平均值,其一般表达式为
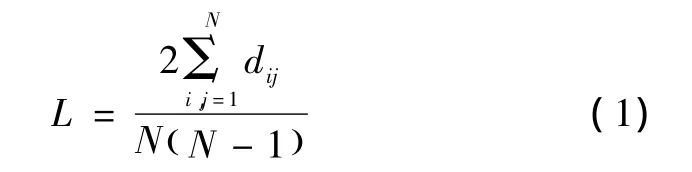
其中:N为网络节点数。网络的平均路径确定了网络中任一对节点间的最具有代表性的路径长度,在现实网络中一般当平均路径小时,信息交换的速度愈加快捷[6]。
5)聚类系数。节点的聚类系数定义为与该节点连接的各节点之间实际存在的边数和总的可能的边数之间的比值,其一般表达式为
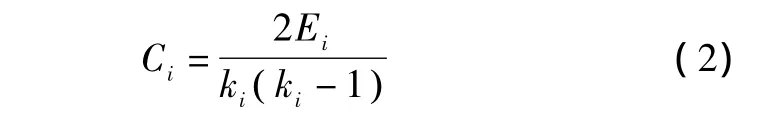
整个网络的平均聚类系数定义为

其中:Ei是实际存在的边数。整个网络的聚类系数C就是所有节点聚类系数的平均值。在现实网络中一般当聚类系数大时,个体之间的联系愈加紧密[7]。
3.2 航母编队舰机协同防空作战系统信息网络物理连接拓扑结构
以美国典型航母编队为例进行分析,以一次防空作战过程为作战想定,假设航母编队中参加作战的有1艘航母、6艘巡洋舰或驱逐舰、20架舰载战斗机、1架预警机,航母编队的指挥控制网络,将编队范围内的各防空作战平台连成一个开放、动态、实时的复杂网络。若该网络中两个节点存在(有线或无线的)通信链路,则认为这两个节点存在物理连接。将美军航母编队作战系统中的各种传感器、指挥控制台、通信设备和武器装备抽象成节点,各节点之间的信息传输抽象成边时,整个系统可以看成一个网络,航母的各种传感器、指挥控制台、通信设备和武器装备等节点共有70个,如表1所示。“提康德罗加”级巡洋舰(舰艇群指挥所)的节点有42个,“伯克”级与“斯普鲁恩斯”级驱逐舰的节点有34个,E-2C预警机的节点有31个,F/A-18战斗机的节点有30个[8],限于篇幅原因,不详细列举。画出该网络的拓扑结构如图4所示。

表1 航母防空节点Table 1 The air defense nodes of aircraft carrier
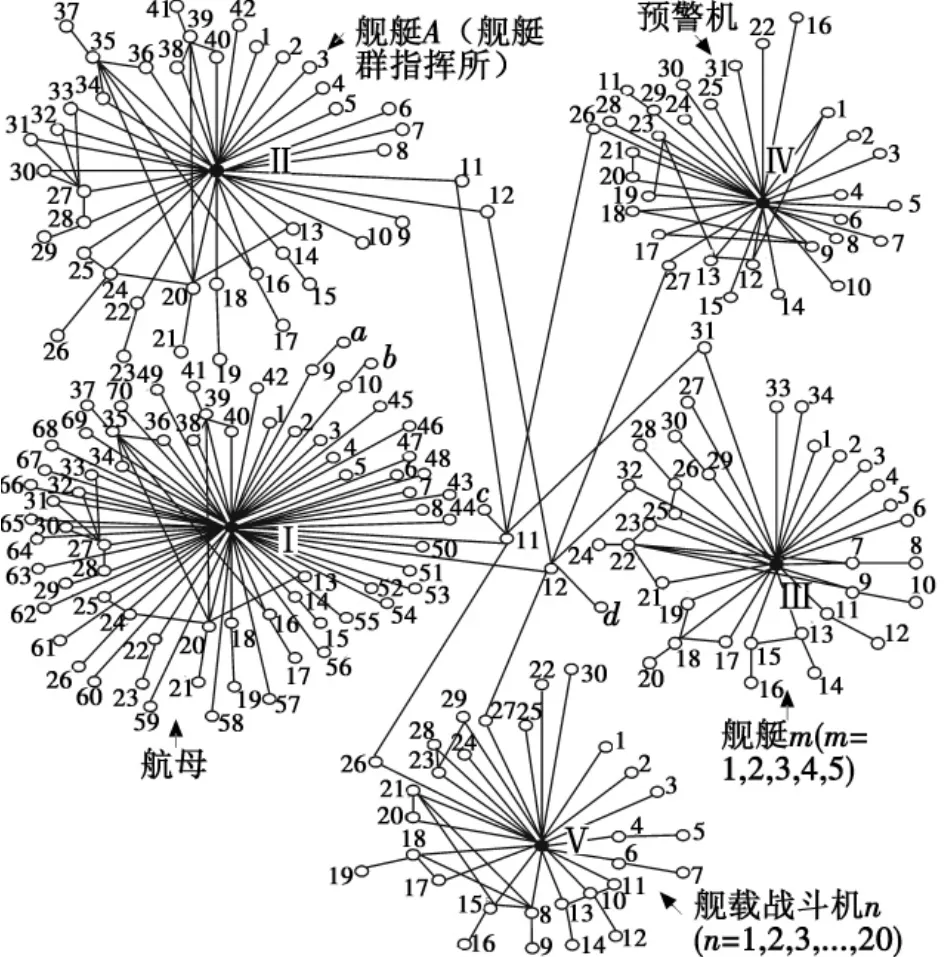
图4 舰机协同防空作战系统网络的拓扑结构Fig.4 Topological structure of warship-aircraft cooperated air defense operation system network
图中节点旁边的数字表示节点的序号,黑色节点分别表示航母、驱逐舰、预警机、舰载机的网络交换机。该网络通过节点a、b、c、d与岸指或友邻兵力进行通信。
3.3 航母编队作战系统信息网络仿真结果及静态特性分析
由图4可以得到编队作战系统信息网络节点度的统计数据,如表2所示。

表2 编队作战系统信息网络节点度的统计数据Table 2 Degree statistical data of formation operation system information network nodes
根据表2得到的数据,分别得到节点的度分布在笛卡尔坐标系和对数坐标系下随节点数变化,如图5和图6所示。

图5 笛卡尔坐标下度分布随节点度数变化Fig.5 Nodes'degree distribution vs degree value in Cartesian coordinates
综合分析上述结果,可以得出编队的作战系统网络具有如下复杂性特征。
1)连接结构的复杂性。航母编队舰机协同防空作战系统信息网络的连接结构既非完全规则也非完全随机。观察表1,48.4%的节点的度为1,而占网络节点总数2.9%的28个节点(分别为编队中1艘航母、6艘舰艇、1架预警机和20架舰载战斗机的网络交换机)却占有网络的绝大部分连接。同时从图5看出,编队作战系统信息网络的度分布随节点度数是一条递减的曲线,虽然网络中节点数比较少,但其对数坐标下网络节点的度分布仍接近幂率分布(幂指数γ≈1.49),如图6所示,因而可判断该网络具有无尺度网络特性[7]。
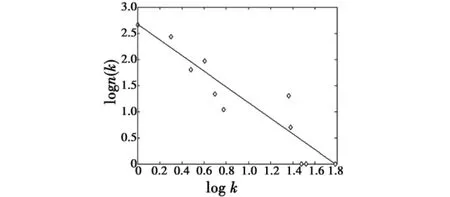
图6 对数坐标下度分布随节点度数变化Fig.6 Nodes'degree distribution vs degree value in logarithm coordinates
2)网络的小世界特性。由式(1)算出该网络的平均路径长度L=2.864。由式(2)、式(3)算出网络的聚类系数C=0.188。可见该网络是一个具有小的平均路径长度和大的聚类系数(C=0.188算是较大的)的小世界网络[7]。
3)网络连接的稀疏性。在图4中,航母编队作战系统信息网络节点有942个,而边却只有2437条,一个有N个节点的具有全局耦合结构的网络的节点连接数目为O(N2),而该作战系统信息网络的连接数目通常为O(N),所以该作战系统信息网络跟大多数实际网络一样都是很稀疏的[7]。
4 编队作战系统复杂网络特性分析及结论
航母编队防空作战系统信息网络构成了一个复杂网络,具有复杂网络的很多典型的特性,这些特性可以揭示航母编队舰机协同防空作战效能提升的规律。
4.1 无尺度特性分析
航母编队的作战系统具有无尺度特性。无尺度网络对随机节点故障具有极高的鲁棒性,因为其网络的度分布具有极端的非均匀性:绝大多数节点的度都非常小,而有少量节点的度相对很大[9]。在实际作战中,受敌攻击随机崩溃的节点大都是度很小的节点,去掉这些节点对整个网络的连通性不会产生大的影响。然而,正是这种非均匀使得无尺度网络对蓄意攻击具有高度的脆弱性:有意识地攻击网络中极少量度最大的节点(如中心交换机)就会破坏整个网络的连通性,该网络将处于崩溃状态,因此应重点保护好中心交换机。
从图4中可以直观地看出,该模型多数节点的连接数很少,而少数节点的连接数很多,故该网络存在少量的“关键”节点和大量的“末梢”节点。这种现象既与复杂网络无尺度的基本特性一致,又符合指挥控制系统的设计规范,如高一级的指挥控制单元具有更多的指挥和感知的职责优势,故连接具有一定的聚集性,而像末端的雷达等战场感知单元仅负责向上一级汇报或在小范围内共享信息,故节点度很小。度分布反映了网络拓扑中节点的连接情况,也是区别于随机网络和规范网络的重要特征之一。对该网络的度进行统计,其结果如图4所示,从图中可以看出,笛卡尔坐标系下,信息系统网络的度分布虽然呈现一定的不均匀性,但对数坐标系下度分布的幂律分布则相对清晰些,使用非线性最小二乘法拟合其度分布曲线,可以得出尺度因子值为1.49,但同时发现其耦合效果并不是特别理想,一方面可能与实验数据的统计规模有关,另一方面也可能是系统无尺度程度不高的原因。
4.2 小世界特性分析
航母编队的作战系统具有小世界网络特性。这种既具有较短的平均路径长度又具有较高的聚类系数的网络,在实际作战中,某种武器装备被攻击(即某个节点被破坏)后,若重新连接该武器装备的概率很小,网络的平均路径长度将下降很快,若能重新连接,得到的网络与原始的网络的局部属性差别不大,从而网络的聚类系数变化也不大。在紧张的实战中若非必要可不用立即连接该武器装备。
拓扑图对应的网络平均路径长度L=2.864,聚类系数C=0.188,可以看出:网络的平均路长较短,这主要与部队“扁平化体制”需求有关,直接缩短了信息处理和传达的步骤;同时,网络的聚类系数相对较大,这与加强舰艇与飞机作战平台协同作战与信息共享有着直接的关系。通过与文献中收集的各种网络拓扑相应的参数进行比较可以发现[10]:该网络与小世界现象的特性要求基本近似。
航母舰艇编队舰机协同防空作战系统信息网络的优点主要表现在以下几点。
1)网络的时效性强。由上面的分析,我们知道航母编队作战系统信息网络具有小世界特性,主要体现在网络的平均路径长度短,网络的聚类系数比随机网络要大很多,使得网络的连接性比随机网络要好很多,这样有利于信息在网络中的传播,使得在很短时间内经过很少的“跳数”,就能够从一个节点到达另一个节点。
2)安全部署方便。由于航母编队作战系统信息网络是一个非均匀网络,使得网络对于随机故障的鲁棒性很高。它所面临的最主要威胁是来自对其关键节点的选择性攻击。所以在进行安全部署时,着重保护这些关键节点应做到:增加关键节点的冗余度;适当增加关键节点的带宽,提高关键节点的处理速度;在对网络进行病毒预防时,对关键节点进行免疫等等。这样可以充分利用网络本身的特点,顺应网络的进化趋势,达到事半功倍的效果。
航母编队舰机协同防空作战系统信息网络的缺点主要表现为以下两点。
1)网络抗毁性差。由于航母编队作战系统的非均匀特性,使得网络存在少量的关键节点(集散节点),它们具有很高的连接度,在整个网络中具有举足轻重的作用。一旦这些关键节点(集散节点)故障或被攻击,就足以使整个网络崩溃。这是非均匀网络的致命缺陷[11]。
2)病毒传播性强。由于集散节点连接很多其他节点,所以任何一个遭受病毒入侵的节点,都可能感染到网络中的集散节点。而一旦集散节点被感染,它就会把病毒传播给众多的其他节点,这就导致了病毒迅速在整个网络里传播。
5 结语
本文分析了航母编队舰机信息协同网络的结构,列举了指挥控制系统中信息的分类,把网络复杂性理论应用于航母编队舰机信息协同的研究,分别建立平台中心防空作战模式和舰机协同防空作战模式的信息协同模型,通过数学推理进行定量计算,从拓扑结构对航母编队作战系统信息网络的静态几何量进行了研究。航母编队作战系统信息网络是一个动态的网络,下一步还可以对航母编队作战系统信息网络演化动力学性质、网络演化性质、网络演化机制、网络结构的稳定性等方面进行深入研究。
[1]李相民,张安,张耀中.空袭中防方已知攻方编队数量情况下的效能评估[J].电光与控制,2008,15(4):1-4.
[2]徐圣良,姜青山,张培珍.舰机协同防空作战理论的研究与进展[J].舰船科学技术,2010,32(7):135-139.
[3]阳曙光,时剑,李为民.联合火力打击协同式指挥控制模式及其军事概念建模[J].电光与控制,2008,15(2):1-4.
[4]张翔,黄俊,魏贤智.多批编队目标的实时火力分配决策[J].电光与控制,2008,15(4):31-33.
[5]姚宗信,李明,陈宗基.多机协同作战任务决策方法多智能体结构框架[J].电光与控制,2008,15(3):1-4.
[6]汪小帆,李翔,陈关荣.复杂网络理论及应用[M].北京:清华大学出版社,2006.
[7]ALBERT R,BARABASI A.Emergence of scaling in random networks[J].Science,1999,286(15):509-512.
[8]刘永辉.国外航空母舰作战指挥[M].北京:军事科学出版社,2007.
[9]朱涛,常国岑,施笑安.网络中心战的无尺度特性研究[J].电光与控制,2008,15(2):5-7.
[10]ALBERT R,BARABASI A L.Statistcal mechanics of complex networks[J].Reviews of Modern Physics,2002,74(1):47-97.
[11]吴金闪,狄增如.从统计物理学看复杂网络研究[J].物理学进展,2004,24(1):19-20.

