无砟轨道垂向高频振动响应分析＊

刘林芽，吕 锐，刘海龙

(华东交通大学铁路环境振动与噪声教育部工程研究中心，江西南昌 330013)

无砟轨道垂向高频振动响应分析＊

刘林芽，吕 锐，刘海龙

(华东交通大学铁路环境振动与噪声教育部工程研究中心，江西南昌 330013)

为了分析不平顺条件下无砟轨道的高频振动特性及声辐射特性，建立了高速铁路无砟轨道车辆－轨道垂向耦合动力学模型，在轮轨表面粗糙度激励下考虑接触滤波，模拟出了轮轨垂向高频振动相互作用力，并将此力作用在按我国实际轨道结构建立的三维实体有限元模型上，仿真模拟轨道系统在随机荷载作用下的高频振动特性，得到了钢轨轨头、轨腰、轨底3处的振动响应与轨道板同一截面离钢轨不同距离的3处振动响应和竖向振动加速度级谱。结果表明:钢轨振动响应中轨头处振动响应最大，轨道板振动响应中距离钢轨越近响应也越大;在计算频域内轨道系统的高频振动主要以钢轨的振动为主，钢轨高振幅的振动主要集中在0～3 000 Hz，而轨道板的高振幅振动就主要集中在0～1 000 Hz，这为以后采用三维轨道结构面上的振动响应结果作为速度边界条件，利用声学边界元法计算轨道的声辐射奠定了基础。

高频振动;振动响应;无砟轨道;有限元模型

相对传统有砟轨道，无砟轨道以其诸多优点在国内外得到广泛应用，其中高速列车与无砟轨道产生的噪声问题受到了高度重视。在高速铁路上，轮轨滚动噪声是高速铁路的主要噪声，而滚动噪声实际上就是轮轨之间的高频振动造成的。Remington［1］从轮轨相互作用角度出发，在轮轨系统动力特性分析的基础上，建立了轮轨滚动噪声预测模型;Thompson 等［2－3］对 Remington 的模型进行了发展，考虑了更详细的轮轨接触关系，并将钢轨模型扩展为轨道模型;国内也有学者针对轮轨特点建立了轨道系统高频振动模型，分析了轨道系统高频振动特性［4－5］。本文运用车辆－轨道垂向耦合动力学理论，将车辆与板式轨道作为一个整体系统，建立了车辆与板式轨道垂向相互作用的动力学分析模型，以轮轨表面粗糙度作为激励源，并考虑轮轨接触滤波，得到在轮轨粗糙度激励下轮轨垂向高频振动相互作用力，分析了轨道系统的三维有限元模型在此垂向力作用下的垂向高频振动特性。为以后利用声学边界元法将有限元振动响应结果作为边界条件，计算轨道系统的瞬态声辐射量奠定了基础［6］。本文研究线路见图1。

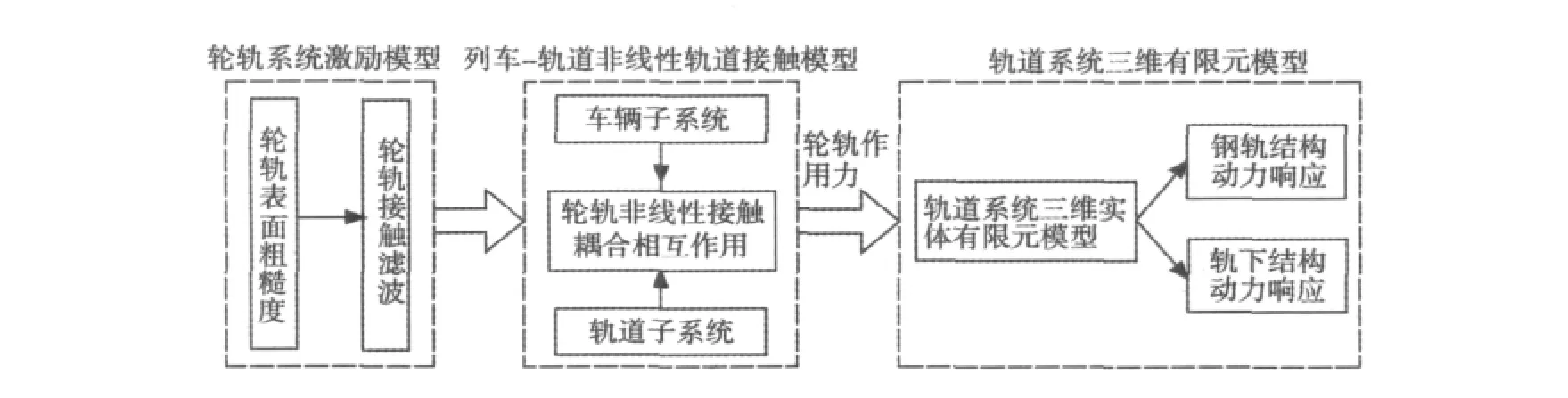
图1 研究线路图Fig.1 The circuit diagram

1 无砟轨道车辆－轨道垂向耦合动力学模型

运用车辆－轨道耦合动力学原理，将车辆和板式轨道作为一个整体系统建立了无砟轨道垂向耦合动力学模型，如图2所示。车辆系统中车体、构架、轮轴视为多刚体系统，车辆结构部件之间考虑由弹簧、阻尼元件连接;轨道系统中钢轨采用连续弹性离散点支承无限长Timoshenko梁模型，轨下胶垫(含扣件)以离散分布的粘滞阻尼和线性弹簧表示;轨道板被视为连续均布弹性基础上的自由梁，板下沥青垫层的弹性阻尼则用连续分布的阻尼和线性弹簧表示。车辆与板式轨道的垂向耦合作用通过轮轨接触来实现，轮轨力按Hertz非线性弹性接触理论进行处理。

图中:Mc和Jc为车体的质量与转动惯量;Mt和Jt为转向架的质量与转动惯量;ks1和ks2为车辆一、二系悬挂刚度;cs1和cs2为车辆一、二系悬挂阻尼;Mwi(i=1，2，3，4)为第i个车轮的质量;vc和θc为车体沉浮振动的竖向位移、车体点头振动的角位移;vti和θti(i=1，2)为前、后转向架沉浮振动的竖向位移、点头振动的角位移;vwi(i=1，2，3，4)为第i个车轮的竖向位移。

图2 车辆－轨道垂向耦合动力学模型Fig.2 Vehicles－ unballasted track vertical coupling dynamics model

1.1 上部车辆系统

上部结构为附有二系弹簧系统的整车模型，车体和转向架考虑沉浮振动和点头振动，车轮考虑沉浮运动，各振动微分方程详见文献［7］。最后可得上部车辆系统有限元振动响应方程:

式中:［M］u，［C］u和［K］u分别为上部结构的质量、阻尼、刚度矩阵;{q}u，{˙q}u和{¨q}u分别为上部结构的位移、速度、加速度矢量;{P}u为上部结构荷载矢量。

1.2 下部轨道系统

1.2.1 钢轨振动方程

板式轨道由于其结构左右对称，故可取一股轨道进行研究，钢轨视为Timoshenko梁，考虑其剪切与旋转。当列车在轨道上运行时，钢轨在轮轨力Pi和轨道板扣件作用力Rj的共同作用下，得到钢轨垂向位移vr的振动偏微分方程:

式中:ErIr为钢轨的抗弯刚度;mr为单位长度钢轨质量;vs为轨道板竖向位移;v0为车轮静压量;xpi为各车轮坐标;xj为扣件坐标;Nw为轮对数;NS为扣件数。

1.2.2 轨道板振动微分方程

根据弹性基础上梁和板计算的一般规定，当结构物的长度小于其宽度的3倍时，应当作板计算，而在长度大于3倍宽度的情况下则可当作梁计算。据此，可以将对应于单股钢轨的轨道板简化为弹性地基梁上的自由梁［8－9］。轨道板支承在有阻尼的弹性基础上其振动微分方程为:

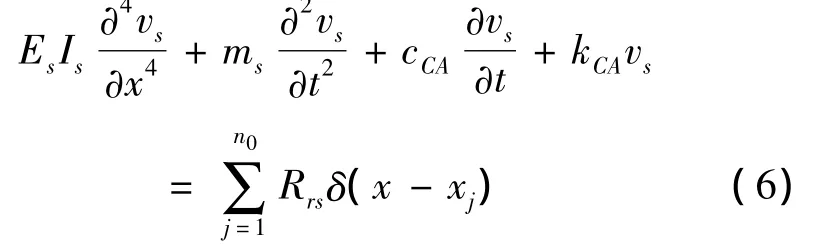
式中:ESIS为轨道板的抗弯刚度;ms为单位长度轨道板质量;cca和kCA分别为轨道板下CA砂浆垫层沿长度方向的分布阻尼和刚度;n0为单块轨道板上单股钢轨的支点数;Rrs为钢轨支点反力;δ为Diraeδ函数。

由式(2)～(6)得出下部轨道子系统的有限元振动响应方程:

式中:［M］l，［C］l和［K］l分别为下部结构的质量、阻尼、刚度矩阵;{q}l，{˙q}l和{¨q}l分别为下部结构的位移、速度、加速度矢量;{P}l为下部结构荷载矢量。

1.3 轮轨耦合

对轮轨动态相互作用关系的描述采用了动态轮轨关系模型，轮轨之间耦合采用Hertz非线性弹性接触理论［10］。

2 激励模型

2.1 轮轨表面粗糙度谱

至今为止，我国尚没有适合轮轨高频振动及轮轨噪声预测的短波轮轨联合粗糙度谱，在轮轨噪声研究中只能借用已有的拟合公式。徐志胜等［11］应用Sato谱作为轮轨表面粗糙度公式对轮轨高频振动进行了研究，获得较为可靠的结果，在此，将Sato谱作为轮轨表面粗糙度的激励源，拟合公式解析表达式如下［12］:

式中:k为粗糙度波数;A为轮轨表面粗糙度系数，A=4.15×10-8～5.0×10-7。

2.2 轮轨表面粗糙度输入模型

由于采用Herzt非线性接触理论描述轮轨接触，表面粗糙度谱不能直接输入系统，必须以时序样本的方式输入。为此，首先必须将表面粗糙度空间谱密度通过时频转换的方法转换为时序样本，即根据功率谱分别求出频谱的幅值和随机相位，然后再通过傅立叶逆变换得到轮轨表面粗糙度时域模拟样本［13］。

2.3 轮轨接触滤波

因为轮轨表面粗糙度对轮轨的激励作用与接触斑大小有关，当粗糙度波长小于接触斑时，其激励作用将削弱，这种轮轨接触区的特性称为轮轨接触区滤波作用，为了考虑这种影响，通常引入滤波函数 ，其解析表达式如下［14］:

式中:b为接触区圆半径;k为粗糙度波数;α为粗糙度相关系数;J为贝塞尔函数。

最后模拟得到了Sato谱的时域序列，如图3所示。

图3 Sato谱时域系列Fig.3 Sato spectral time－domain series

2.4 计算结果

运用Newmark法求解系统振动方程组，并采用计算机编程数值模拟求解，得到轮轨力时程曲线图如图4所示。可以看出轮轨接触力时程曲线是围绕列车单轮重70 kN来回振荡，这也说明了所计算轮轨接触力的合理性与可行性。列车采用CHR3－380型动车，钢轨为 P60轨，轨道板是CRTSⅡ型板，列车时速300 km/h，其他参数均取自文献［15］。

图4 轮轨垂向接触力时程曲线图Fig.4 Wheel－ rail vertical force －time curve

3 轨道结构有限元模型及其高频振动分析

3.1 轨道结构有限元模型

运用大型通用有限元软件根据我国轨道实际结构建立轨道系统的三维实体有限元模型，钢轨、轨道板采用三维实体单元SOLID45进行模拟;扣件系统、CA砂浆层采用COMBIN14单元进行模拟，如图5所示。

图5 轨道系统三维有限元模型Fig.5 Finite element model of rail system

3.2 轨道结构高频振动响应分析

将2.4中计算得到的垂向轮轨力加载到三维有限元模型上，并对其进行移动荷载瞬态分析，之后分别提取钢轨和轨道板跨中节点计算结果。

对钢轨的轨头、轨腰和轨底进行研究比较，取点位置如图6，其时间位移响应曲线如图7。结果表明，钢轨在垂向激励作用下，轨头处位移最大为1.04 mm，其次是轨底处位移为 0.91 mm，最小位移是轨腰处位移为0.87 mm，3处位移相差不大，且轨头处响应最大，那么钢轨的加速度响应可用最大的轨头处加速度响应表示，见图8。

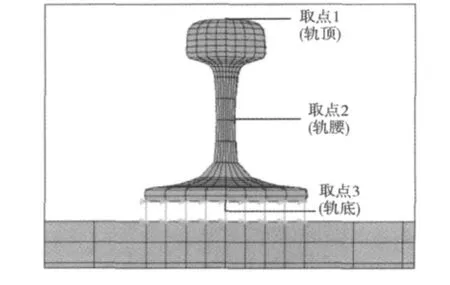
图6 钢轨取点位置截面图Fig.6 The section graph fetch points position of rail

图7 钢轨垂向位移时间曲线Fig.7 Vertical displacement－ time curve of rail

图8 钢轨垂向振动加速度曲线Fig.8 Vertical acceleration － time curve of rail

对轨道板进行动力响应分析，观察点选取如图9，其位移时间响应曲线如图10。结果表明，轨道板同一截面上距离钢轨最近的振动响应最大，距离越远响应越小，其中最大响应值为0.48 mm，那么轨道板的加速度响应可用最大的点1处加速度响应表示，见图11。

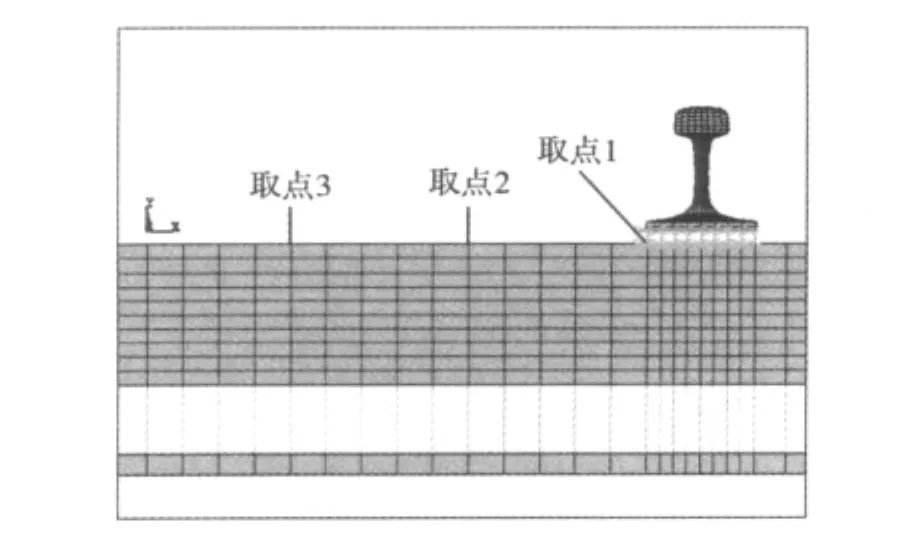
图9 轨道板取点位置截面图Fig.9 The section graph fetch points position of track slab

图10 轨道板垂向位移时间曲线Fig.10 Vertical displacement－ time curve of track slab

图11 轨道板垂向振动加速度曲线Fig.11 Vertical acceleration － time curve of track slab

由图8、图11分析钢轨轨头处和轨道板1点处垂向的加速度响应，发现钢轨最大竖向加速度为182.23 m/s2，轨道板的最大竖向加速度值为25.49 m/s2。

为了给在垂向轮轨力作用下轨道系统的瞬态声辐射量提供计算依据，对钢轨和轨道板的高频振动响应进行了计算［12］。将图8、图11结果进行时频转换，得到了钢轨以及轨道板的竖向振动加速度级谱，如图12～图13所示，加速度参考值取为0.001g。

由图12可知，900，1 800和3 000 Hz时钢轨加速度级谱有峰值，波谷出现在1 200，2 500 Hz，可以看出钢轨高振幅的振动集中在0～3 000 Hz，在更高的频域范围内由于波数过滤器作用很强，钢轨的振动加速度并不突出。

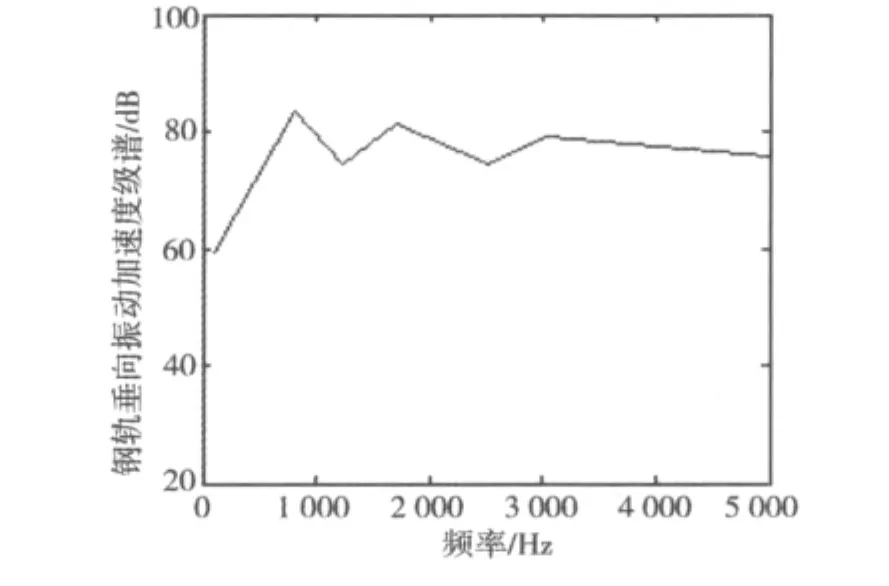
图12 钢轨竖向振动加速度级谱Fig.12 The vertical vibration acceleration spectrum level of rail

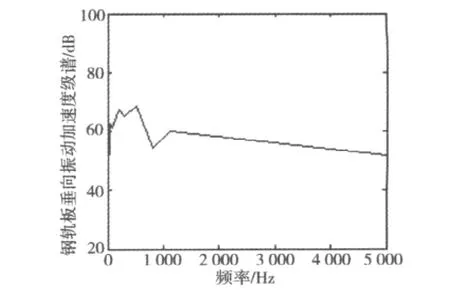
图13 轨道板竖向振动加速度级谱Fig.13 The vertical vibration acceleration spectrum level of track slab

从图13可得知，轨道板振动加速度级谱的多数波峰和波谷主要集中在0～1 000 Hz，在700 Hz时存在一个较大的波峰，这说明轨道板主要还是以低频振动为主，对高频部分的贡献很少且高频振动的衰减很快。

综上所述，在高频范围内(＞1 000 Hz)轨道系统的振动主要是以钢轨的振动为主，且符合国内外研究者在高频振动与声辐射之间的关系所做出的结论与成果［16］。所以可以预测在接下来的声辐射计算中，轨道系统的声辐射也是以钢轨引起的声辐射为主。

4 结论

(1)运用车辆－轨道垂向耦合动力学理论，在轮轨表面粗糙度激励下考虑接触滤波，模拟出了轮轨随机粗糙度谱情况下轮轨垂向高频振动相互作用力，根据我国实际轨道结构，建立轨道系统的三维实体有限元模型，以轮轨垂向作用力为激励，分析了轨道系统的振动和频率响应特性;

(2)建立成熟的二维车辆－轨道耦合动力学计算模型，可以有效计算出粗糙度激励下的轮轨垂向作用力，建立的三维轨道实体有限元模型可以计算出轮轨垂向作用力下的轨道结构面上的振动，为以后采用三维轨道结构面上振动响应结果为边界条件，利用声学边界元法计算轨道的声辐射奠定基础;

(3)在计算频域内轨道系统的高频振动主要以钢轨的振动为主，钢轨高振幅的振动主要集中在0～3 000 Hz，在更高的频域范围内由于波数过滤器作用很强，钢轨的振动加速度并不突出，而轨道板的高振幅振动就主要集中在0～1 000 Hz。

［1］Remington P J.Wheel/rail noise，Partl:ehara eterization of the wheel/rail dynamie system［J］.Journal of Sound and Vibration，1976(46):359 －379.

［2］Thompson D J.Wheel－ rail noise generation，Part IV:eontaet zone and results［J］.Journal of Sound and Vibration，1993，161(3):447 －466.

［3］Thompson D J，Jones C J C.A review of the modelling of wheel/rail noise generation［J］.Journal of Sound and Vibration，2000，231(3):519 －536.

［4］魏 伟，翟婉明.轮轨系统高频振动响应［J］.铁道学报，1999，21(2):33 －36.

WEI Wei，ZHAIWan-ming. DynamicResponseof Wheel/Rail System to High Frequency Excitation［J］.Journal of the China Railway Society，1999，20(2):33 －36.

［5］刘林芽，雷晓燕.轮轨系统高频振动研究［J］.中国铁道科学，2004，25(2):52 －55.

LIU Lin-ya，LEI Xiao-yan.Study on high frequency vibration of wheel/rail system［J］.China Railway Science，2004，25(2):52 －55.

［6］陈 嵘，王 平.客运专线无碴轨道噪声问题探讨［J］.铁道科学与工程学报，2006，3(5):60 －63.

CHEN Rong，WANG Ping.Discussion on noise of passenger dedicated railway line non － ballasted track［J］.Journal of Railway Science and Engineering，2006，3(5):60－63.

［7］雷晓燕.铁路轨道结构数值分析方法［M］.北京:中国铁道出版社，1998.

LEI Xiao-yan.Numerical analysis of railway track structure［M］.Beijing:China Railway Publishing House，1998.

［8］向 俊，赫 丹.高速列车与博格板式轨道系统竖向振动分析模型［J］.交通运输工程学报，2007(3):1－5.

XIANG Jun，HE Dan.Analysis model of vertical vibration of high － speed train and Bgle slab track system［J］.Journal of Traffic and Transportation Engineering，2007(3):1－5.

［9］雷晓燕，张 斌，刘庆杰.列车－轨道系统竖向动力分析的车辆轨道单元模型［J］.振动与冲击，2010，29(3):168－173.

LEI Xiao-yan，ZHANG Bin，LIU Qing-jie.Model of vehicle and track elements for vertical dynamic analysis of vehicle－ track system［J］.Journal of Vibration and Shock，2010，29(3):168 －173.

［10］刘林芽，雷晓燕，练松良.轨道交通轮轨滚动噪声的预测［J］.振动与冲击，2007，26(12):146 －150.

LIU Lin-ya，LEI Xiao-yan，LIAN Song-Hang.Prediction of wheel/rail rolling － noise during rail transit［J］.Journal of Vibration and Shock，2007，26(12):146 －150.

［11］徐志胜，翟婉明.轨道交通轮轨噪声预测模型［J］.交通运输工程学报，2005，5(3):14 －19.

XU Zhi-sheng，ZHAI Wan-ming.Prediction model of wheel－ rail noise for rail transit［J］.Journal of Traffic and Transportation Engineering，2005，5(3):14 －19.

［12］Sato Y.Study on high frequency vibration in track operation with high speed trains［J］.Quarterly Reports，1977，18(3):22 －27.

［13］魏 伟，赵兴钢.轮轨振动和噪声的分析［J］.噪声与振动控制，2007(4):99－102.

WEI Wei，ZHAO Xing-gang.Analysis on vibration and noise of vehicle wheel［J］.Noise and Vibration Control，2007(4):99－102.

［14］Remington P J.Wheel/railing noise，I:Theoretical analysis［J］.Journal of the Acoustical Society of America，1987，81(6):1805 －1823.

［15］雷晓燕，圣小珍.现代轨道理论研究［M］.北京:中国铁道出版社，2008.

LEI Xiao-yan，SHENG Xiao-zheng.Advanced studies in modern track theory［M］.Beijing:China Railway Publishing House，2008.

［16］刘林芽，雷晓燕，练松良.铁路轮轨噪声预测分析［J］.噪声与振动控制，2008(2):73 －76.

LIU Lin-ya，LEI Xiao-yan，LIAN Song-hang.Prediction of wheel/rail rolling － noise during rail transit［J］.Journal of Vibration and Shock，2008(2):73 －76.

Vertical high frequency vibration response analysis of ballastless track

LIU Lin-ya，LV Rui，LIU Hai-long

(Engineering Research Center of Railway Environmental Vibration and Noise，Ministry of Education，East China Jiaotong University，Nanchang 330013，China)

In order to analyze the high frequency dynamical and the sound radiation characteristics of unballasted track under an irregularity condition，the paper proposed a vehicle－track vertical coupled model of high－speed railway.Under the incentive of surface roughness and considering contact filtering，the high frequency vertical load between rail and wheels can be calculated.Applying the load on the three dimensional finite element model，based on the rail structure of actual conditions in our country，the high－frequency vibration features of track system under the influence of random vibration loads can be numerically modeled，and the vibration response at the head，waist and base of the rail，the vibration response and vertical vibration acceleration spectrum level of three different sections parallel to the rail plate were calculated.The results show that the biggest vibration response of the rail appears at the rail head while that of the rail plate turn up at the one closer to the rail.The dominate high－frequency vibration of the rail system within the frequency included in the calculation is vibration of rail of which the high amplitude range is 0 ～3 000 Hz，while，as for the rail plate，the range mainly is 0 ～1 000 Hz.The domain provided a foundation for using the calculation result of vibration response on the 3D rail structure as speed boundary and calculating orbit sound radiation by acoustic boundary method.

high frequency vibration;vibration response;ballastless track;finite element model

U213.2

A

1672－7029(2011)06－0001－06

2011－11－16

国家自然科学基金资助项目(51068007);新世纪优秀人才支持计划资助项目(NECT－09－0167)

刘林芽(1973－)，男，江西樟树人，教授，从事铁道及城市轨道交通工程振动与噪声的研究