基于反演理论在役连续刚构桥有效预应力识别＊

张兆宁，贺拴海，赵 煜

(1.长安大学 公路学院，陕西西安 710064;2.兰州理工大学土木工程学院，甘肃兰州 730050)

基于反演理论在役连续刚构桥有效预应力识别＊

张兆宁1，2，贺拴海1，赵 煜1

(1.长安大学 公路学院，陕西西安 710064;2.兰州理工大学土木工程学院，甘肃兰州 730050)

由于受环境、气候、荷载及其他外在因素的共同影响，施加于桥梁结构的预应力也随之发生变化，准确掌握其内部真实的应力状态对保证桥梁的安全运营至关重要。针对这一问题，以反演理论为基础，依据桥梁服役期间结构变位的实际监测结果，由位移反分析法得到了不同时间点梁体内存在的有效预应力数值。以某一预应力混凝土连续刚构桥为例，通过反分析得到的有效预应力为参数，重新建立有限元计算模型，分析了在设计荷载作用下梁体强度及刚度的变化情况。理论结果与实测位移的对比表明，利用反分析法可以较为精确地预测服役期间桥梁内真实的预应力状态。

连续刚构桥;反演理论;目标函数;有效预应力;识别

对已建预应力混凝土梁桥而言，在服役期间由于受到外界不同因素(如荷载、气候、自然灾害等)的共同影响，其原始强度、刚度状态均会产生相应的变化，其表现主要是位移、应力的不断增大。伴随位移场、应力场的不断扩散，梁体一些部位会出现不同程度的开裂损伤等问题，直接影响桥梁的使用性、耐久性及可靠性。为此，国内外学者通过对影响梁体强度、刚度的主要因素的分析研究表明，其中，预应力损失是引起预应力结构受力性能随时间逐渐退化的主要因素之一。目前，对引起预应力损失的成因、组成、解决措施等相关理论研究均比较深入［1－6］。但国内外在成桥状态至不同运营期间梁体实际有效预应力状态方面的相关研究还比较少，如何准确预测及实测出梁体有效预应力仍然是需要深入研究的一个课题。国内规范给出了各种预应力损失的理论计算公式［7］，但对在役预应力混凝土梁桥而言，规范中所提供的计算公式已不能再简单地加以套用。如何确定桥梁运营期间其内部真实预应力状态是亟待解决的一个工程难题。针对这一问题，本文以反演理论为基础，通过实测服役期间桥梁梁体不同时间点主要控制截面测点位移，通过建立相关反分析模型对有效预应力进行了识别，然后依据反演所得结果重新建立分析模型进行正分析，以此来评价在役预应力混凝土桥梁强度及刚度的变化过程。

1 反演基本原理

参数反演问题实际上是一个目标函数的优化问题，它直接利用正分析的过程，通过迭代最小误差函数，逐次修正未知参数的试算值，直至获得最优解［8－11］。将模型输出表示成待求参数的显函数，通过模型输出的量测值，利用函数关系反求出待求参数。对于线弹性问题中，在待求量与量测信息之间建立如下的线形方程组:

式中:［K］为未知量的影响系数阵;{x}为待求未知量阵;{y}为与量测信息有关的已知列阵。

设独立量测信息的总数N，待求未知量总数M，量测信息的最佳估计量Ui与量测值之间的误差为 εi，则有:

由此可知，当量测信息的总数大于待求未知量总数，即N＞M时，可将目标函数定义为:

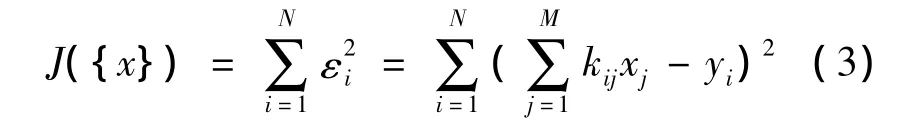
为使目标函数即最佳估计量之间误差的平方和为最小，需要满足的条件为:

将式(4)代入式(3)，利用最小二乘法原理作优化处理后，展开得到其正则方程基本表达式及矩阵形式:

由式(6)可解得直接用于求解材料特性参数的线形代数方程组的普遍表达式:

2 有效预应力反演识别

2.1 目标函数的建立

由于受环境、仪器设备、方法、读数误差等因素的综合影响，现场实测的梁体位移不可避免地存在误差。为了减小误差，量测的数量必须大于待求参数个数，然后通过优化技术得到最优参数值。目标函数的建立是优化反分析的基础，一般表示为系统的实际量测值和模型输出值偏差的某个函数。在预应力混凝土梁桥预应力识别过程中可采用最小二乘法建立如下的目标函数式:

式中:n为梁体实测位移数量;ui为梁体竖向位移实测值;vi为梁体竖向位移理论计算值。

2.2 预应力辨识参数

建立反分析模型以连续介质为基础，钢绞线可以看做是均匀连续非线性介质，其工作状态处于弹塑性范围。由于梁体预应力布置时存在平弯、竖弯及横弯情况，加之梁体构造上的差异，不同梁段处实际预应力损失也有所区别。为了简化分析，假定同一束钢绞线各个位置产生的预应力损失为一恒定值，该值综合体现各项预应力损失的共同影响。对于从整体上分析预应力损失，这种简化是可行的。因此，反分析所得的有效预应力其实为“平均综合有效预应力”，是一个宏观的整体性参数。

2.3 反演计算模型及参数

某一三跨预应力混凝土连续刚构桥(35.0 m+60.0 m+35.0 m)，设计标准为公路 － Ⅰ级，截面形式为单箱单室，主梁混凝土标号为C50，预应力钢筋采用 15.24 mm钢绞线，设计强度1 860 MPa。根据设计资料及施工期间预应力张拉控制规定，有限元分析时初始预应力输入参数取为1 395 MPa。由于梁体位移在运营期间表现为一随机动态变量，为此，通过布设于箱梁1/4中跨、3/8中跨及1/2中跨底板等测点的位移传感器来量测车辆随机通过时的动态位移。然后，将所测位移进行数理统计处理得到各测点平均效应值。为了减少温度对实测结果的影响，测试安排在清晨进行。用于反演计算所需梁体服役期间不同时间点箱梁实测竖向位移如表1所示。对应于式(1～7)，{x}为箱梁实际有效预应力值;{y}为梁体实测位移值。反演计算有限元1/2模型如图1所示。

图1 有限元计算模型Fig.1 Finite element model

表1 箱梁测点竖向位移Table 1 Vertical monitoring deflection of box girder mm

2.4有效预应力反演结果

以ANSYS分析软件为计算平台，以不同时间点实测位移进行反演计算，梁体内有效预应力迭代随次数的变化规律如图2～图7所示。

图2 有效预应力反演迭代变化曲线Fig.2 Inversion iterative chart of effective pre－stress

图3 有效预应力随迭代次数的变化规律Fig.3 Inversion iterative chart of effective pre－stress

图4 有效预应力随迭代次数的变化规律Fig.4 Inversion iterative chart of effective pre－stress

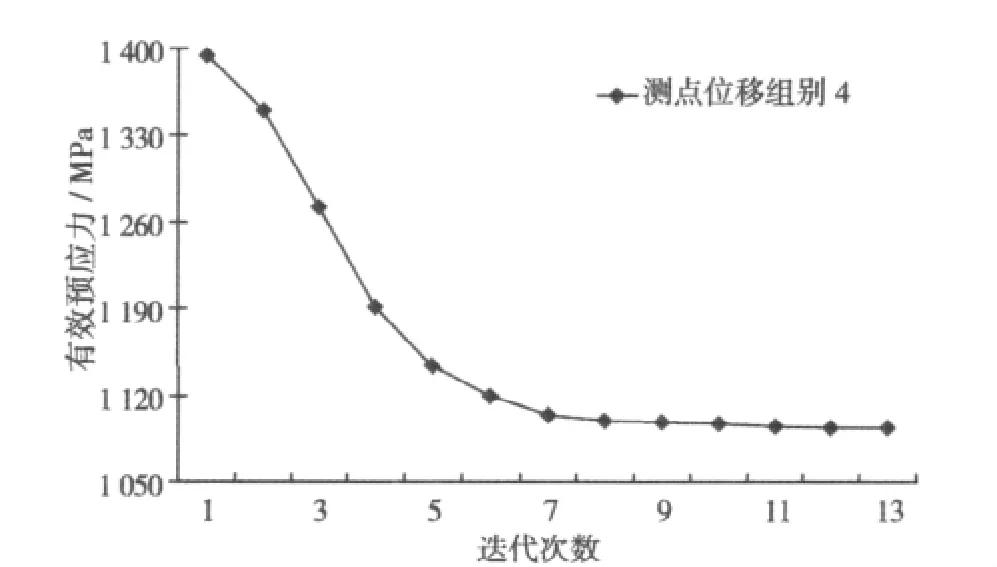
图5 有效预应力随迭代次数的变化规律Fig.5 Inversion iterative chart of effective pre－stress

通过分析计算可知，当中跨跨中实测竖向位移分别为 34.1，36.9，38.8，40.8，44.3 和 46.6 mm时，通过反演分析得到梁体在不同位移下对应的有效 预 应 力 分 别 为 1 261.0，1 191.2，1 144.1，1 094.3 ，1 008.1和 950.4 MPa。对应于上述各种情况下的预应力损失分别为 9.6%，14.6%，18.0%，21.6%，27.7%及 31.9%。

图6 有效预应力随迭代次数的变化规律Fig.6 Inversion iterative chart of effective pre－stress

图7 有效预应力随迭代次数的变化规律Fig.7 Inversion iterative chart of effective pre－stress

3 箱梁强度及刚度分析

以上述反演分析得到的有效预应力为参数，重新建立有限元计算模型进行强度及刚度分析，中跨跨径挠度及底板拉应力随不同预应力的变化曲线如图8～图9所示。

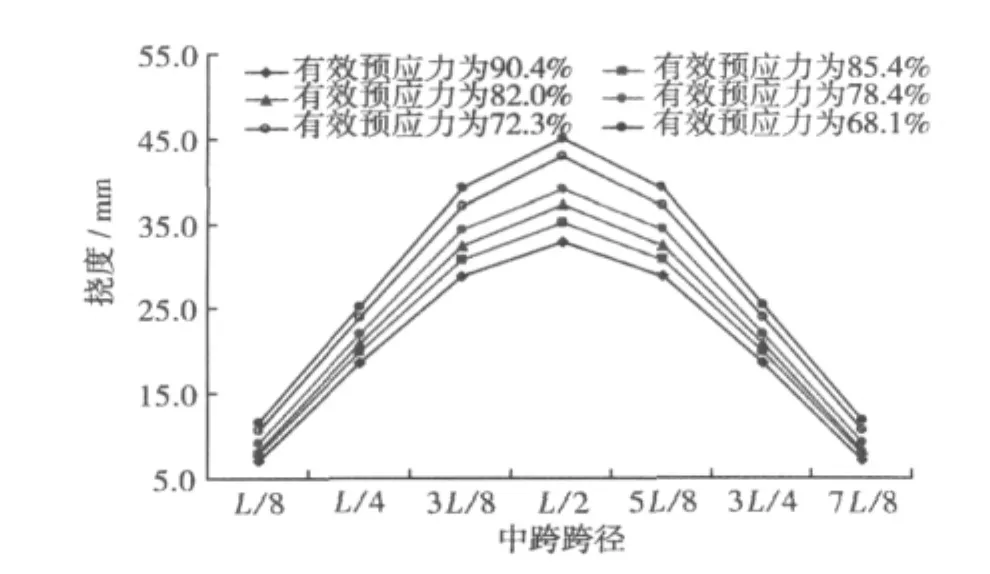
图8 中跨跨径挠度随有效预应力的变化规律Fig.8 Deflection of mid － span with different effective pre－stress

图9 中跨跨径底板拉应力随有效预应力的变化规律Fig.9 Tensile stress of bottom slab for mid － span with different effective pre－stress

通过计算可知，当施加于梁体的有效预应力分别为 90.4%，85.4%，82.0%，78.4%，72.3% 及68.1%时，中跨跨中产生的最大竖向位移分别为32.8，35.1，37.2，39.0，42.9 及 44.9 mm，实测位移与理论分析值最大误差为4.9%。在不同的有效应力作用下，中跨跨径底板最大拉应力分别为1.91，2.05，2.17，2.37，2.52 及 2.63 MPa。

4 结语

以反演理论为基础，通过建立反分析模型，以预应力混凝土箱梁服役期间控制截面实测位移进行位移反分析，计算得到其运营期间不同时间有效预应力值。利用由反演分析所得的数值作为正分析计算时的初始参数，对梁体强度及刚度进行了分析，以此来动态跟踪其应力、位移状态。本文提出的预应力反分析法为在役预应力混凝土梁桥预应力损失识别提供了一条新的思路，可为其承载能力评估提供可靠的参数，以此确保理论分析结果的可靠性及准确性。

［1］任茶仙，竺润祥.连续曲线箱梁预应力效应分析［J］.工程力学，2000，17(4):138 －144.

REN Cha-xian，ZHU Run-xiang.Analysis of prestressing effect for curved continuous box girders［J］.Engineering Mechanics，2000，17(4):138 －144.

［2］张元海，刘世忠.后张法预应力混凝土梁钢束预应力损失研究［J］.中国公路学报，2002，15(2):76 －78.

ZHANG Yuan-hai，LIU Shi-zhong.Study of the loss of pre－stress of tendon in post－tensioned prestressed concrete beams［J］.China Journal of Highway and Transport，2002，15(2):76 －78.

［3］程寿山，李兴庆，于刚勤，等.预应力连续梁桥预应力损失预测及测试方法研究［J］.公路交通科技，2006，23(4):71－73.

CHENG Shou-shan，LI Xing-qing，YU Gang-qin，et al.Research on predication and test method to prestressed a concrete continuous beam bridge［J］.Journal of Highway and Transportation Research and Development，2006，23(4):71－73.

［4］汪劲丰，项贻强，徐 兴.大跨度混凝土桥梁预应力空间效应分析［J］.浙江大学学报，2005，39(1):154－159.

WANG Jin-feng，XIANG Yi-qiang，XU Xing.Research on spatial effect of prestressing force in long－span concrete bridge［J］.Journal of Zhejiang University:Engineering Science，2005，39(1):154 －159.

［5］汪劲丰，项贻强，徐 兴.桥梁空间分析中预应力效应分析方法研究［J］.计算力学学报，2007，24(4):459 －463.

WANG Jin-feng，XIANG Yi-qiang，XU Xing.Numerical simulation of failure process of reinforced concrete specimen under uniaxial tension［J］.Chinese Journal of Computational Mechanics，2007，24(4):459 －463.

［6］李清富，辛保兵，李 科.基于SVM的预应力混凝土梁有效预应力识别［J］.郑州大学学报，2011，32(1):18－21.

LI Qing-fu，XIN Bao-bing，LI Ke.Identification of the effective pre－stress in prestressed concrete beam based on support vector machine［J］.Journal of Zhengzhou University:Engineering Science，2011，32(1):18 －21.

［7］JTG D62—2004，公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京:人民交通出版社社，2004.

JTG D62—2004，Code for design of highway reinforced concrete and prestressed concrete bridges and culverts［S］.Beijin:China Communications Press，2004.

［8］袁 勇，孙 钧.岩体工程优化反演的目标函数［J］.岩土工程学报，1994，16(2):29 －36.

YUAN Yong，SUN Jun.Objective function in optimal back analysis for rock engineering ［J］.Chinese Journal of Geotechnical Engineering，1994，16(2):29 －36.

［9］张路青，贾正雪.弹性位移反分析对地应力、弹模的反演唯一性［J］.岩土工程学报，2001，23(2):172 －177.

ZHANG Lu-qing，JIA Zheng-xue.Inversion uniqueness of elastic displacement back－analysis for ground stress，elastic modulus and poisson’s ratio［J］.Chinese Journal of Geotechnical Engineering，2001，23(2):172 －177.

［10］赵 冰，盛国刚，李 宁.位移反分析的有限元线法及其工程应用［J］.岩石力学与工程学报，2004，23(7):1146－1149.

ZHAO Bing，SHENG Guo-gang，LI Ning.Back analysis method based on finite element method of lines and its application to geo － engineering［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(7):1146 －1149.

［11］孙学先，张 慧.反演理论在悬臂灌筑平弯梁桥线形监控中的应用［J］.工程力学，2007，24(12):135－138.

SUN Xue-xian，ZHANG Hui.Appliance of inversion theory in alignment control of plane curved bridge by cantilever segmental construction［J］.Engineering Mechanics，2007，24(12):135 －138.

Effective pre－stress identification of the continuous rigid frame bridge in service based on inversion theory

ZHANG Zhao-ning1，2，HE Shuan-hai1，ZHAO Yu1

(1.School of Highway，Chang’an University，Xi’an 710064，China;2.School of Civil Engineering，Lanzhou University of Technology，Lanzhou 730050，China)

Due to the environment，climate，loads and other external factors，the pre － stress applied to the bridge is not constant.It is important for engineers to find out the accurate stress condition in order to ensure security of the bridge in service.To solve the problem mentioned above，according to actual monitoring displacement of the bridge in service at different time，the effective pre－stress is obtained by the displacement inversion method based on the inversion theory.Lastly，taking the pre－stressed concrete continuous rigid frame bridge for example，the finite element model with different effective pre－stress is established and the strength and stiffness are analyzed under design load.It is shown from the comparison results of analytical displacements and measured ones that the inverse method is an effective way to predict reasonable pre－stress for the bridge in service.

continuous rigid frame bridge;inversion theory;object function;effective pre－stress;identification

TU448.23

A

1672－7029(2011)06－0012－05

2011－11－16

国家自然科学基金资助项目(50908017)

张兆宁(1978－)，男，宁夏固原人，讲师，博士研究生，从事桥梁结构评价及可靠度研究