多值非扩张非自映射的强收敛定理
董巧丽,邓斌超
(中国民航大学理学院,天津 300300)
多值非扩张非自映射的强收敛定理
董巧丽,邓斌超
(中国民航大学理学院,天津 300300)
对多值非扩张映射构造了两个迭代算法,在自反且严格凸Banach空间中证明了强收敛定理。研究结果推广了Matsushita-Takahashi的结果。
多值非扩张非自映射;自反且严格凸Banach空间;弱序列连续的对偶映射
设E为Banach空间,C是E中的非空子集。令2E为Banach空间E中的所有子集族,CB(E)为E中非空有界闭子集族,K(E)为E中非空紧子集族。设H是CB(E)上的 Hausdorff度量,即
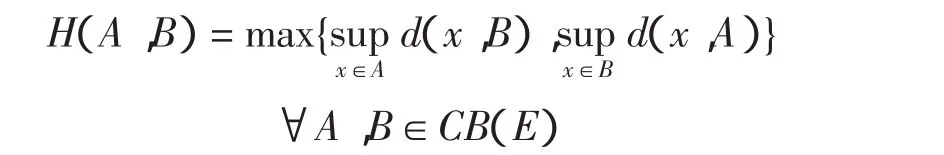
其中:d(x,B)=inf{‖x-y‖;y∈B}。T ∶C→2E称为多值非扩张映射,如果对∀x,y∈C,满足 H(Tx,Ty)≤‖x-y‖。设 F(T)={x∈D(T)∶x∈Tx}是映射 T 的不动点集,其中D(T)是映射T的定义域。
最近Matsushita-Takahashi[1]研究了如下的迭代格式

其中:Q∶E→C是太阳非扩张收缩映射。在本文中把Matsushita-Takahashi的迭代格式(1)、(2)推广到适用于多值映射的算法。设C是Banach空间E的非空闭凸子集,Q∶E→C是太阳非扩张收缩,根据下节引理1,选择适当的 u,x1∈C

其中 yn∈Txn,使得‖yn+1-yn‖≤H(Txn+1,Txn)。假设序列 αn⊂[0,1]满足条件

1 预备知识
设E为实Banach空间,J∶E→2E*为对偶映射,即

其中E*是E的对偶空间并且<·,·>是对偶内积。设C是E中的非空子集,D⊂C,则Q∶C→D称为太阳映射,如果Q(Qx+t(x-Qx))=Qx,其中对∀x∈C和t≥0,有Qx+t(x-Qx)∈C。Q∶C→C称为收缩映射,如果Q2=Q。集合D称为集合C上的太阳非扩张收缩,如果存在一个从集合C到集合D上的太阳非扩张收缩映射。
设C是光滑Banach空间中的非空闭凸子集,Q是E到C上的太阳非扩张收缩,则Q唯一。由于∀y∈C,对于映射T∶C→E,引入条件

其中:Sx={y∈K(E)∶y≠x,Qy=x};是 Sx的补集;Q是E到C上的太阳非扩张收缩。
引理1 设X是完备度量空间,且A,B∈K(X)。则∀a∈A,存在 b∈B,满足[2]
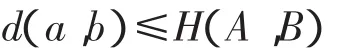
引理2 设an是非负实序列且满足
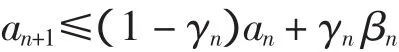
其中序列{γn}⊂(0,1)和序列{βn}⊂R,满足

引理3 设C是光滑Banach空间E中的闭凸子集,设T∶C→E是非扩张映射。假设C是E上的太阳非扩张收缩,且满足式(5),则 F(T)=F(QT)[1]。
引理4 设C是严格凸Banach空间E中的闭凸子集,设T∶C→E是非扩张映射。假设C是E上的太阳非扩张收缩。如果 F(T)≠Ø,则映射 T满足式(5)[1]。
引理5 设C是光滑Banach空间E中的非空闭凸子集,D⊂C,J∶E→E*是 E 上的对偶映射,P∶C→D是一个收缩。成立如下等价条件:
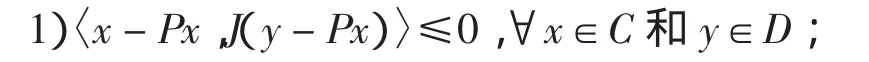
2)P既是太阳映射也是非扩张映射。
定义如下隐格式
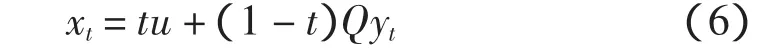
其中 yt∈Txt。

2 主要结论
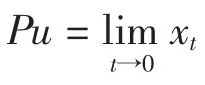
定理2 设E是自反的严格凸Banach空间且E有弱序列连续的对偶映射。C是E中的非空闭凸子集,T∶C→K(E)是非扩张映射。设C在E上太阳非扩张收缩。假设 F(T)≠Ø 满足 T(y)=y,∀y∈F(T),序列 αn满足条件 H1)~H3),则由式(3)定义的序列 xn→Pu,n→∞,其中 P ∶C→F(T)=F(QT)是唯一的太阳非扩张收缩映射。
证明 第一步证明:QT是非扩张多值映射,即
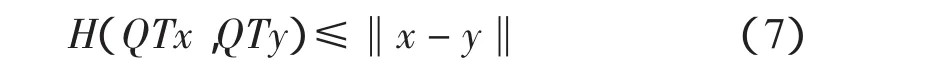
因为Q和T是非扩张映射,可得
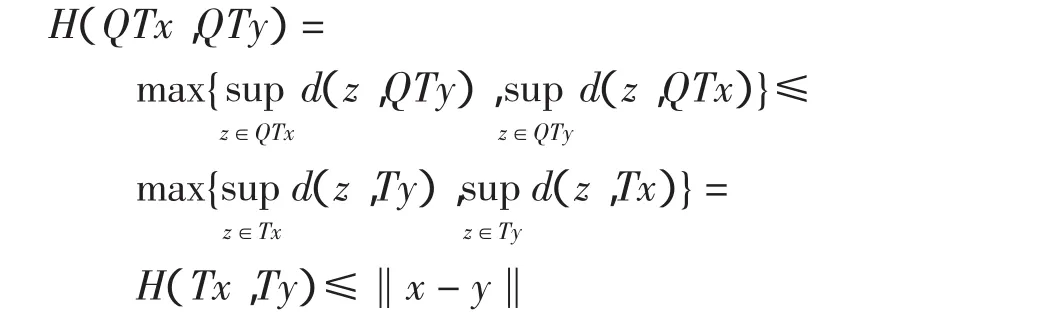
根据引理 3,可取 z∈F(T)=F(QT),根据定理条件有z=Tz。由 yn∈Txn,可得

其中 M=max{‖u-z‖,‖x0-z‖},因此序列 xn,yn和Qyn有界。则可得
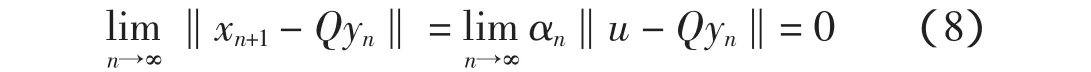
第二步证明
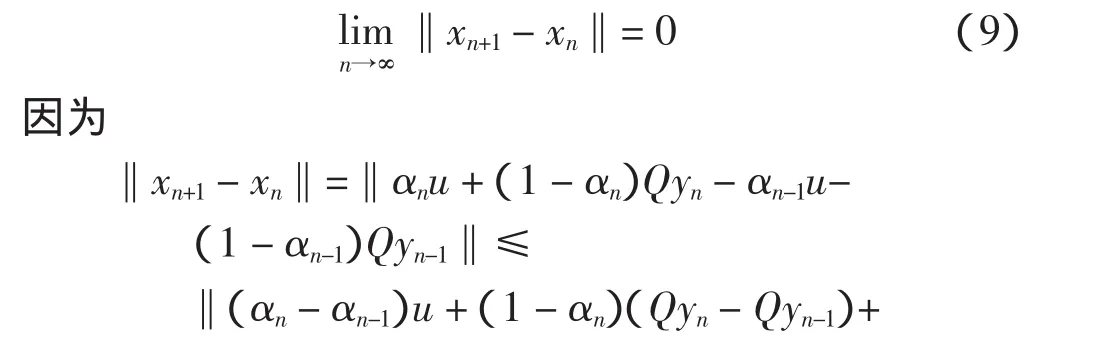

由 yn∈Txn,可得 Qyn∈QTxn,因此有
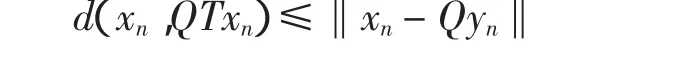
联立式(8)、式(9)和上式,得
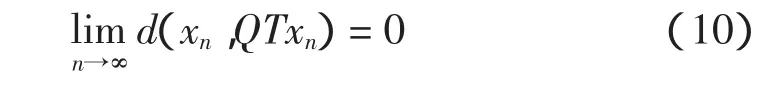
据定理1,可知F(T)是K上的太阳收缩且P∶K(E)→F(T)是唯一的太阳非扩张收缩映射。
第三步证明

取序列xn+1中的子列xnk+1,满足
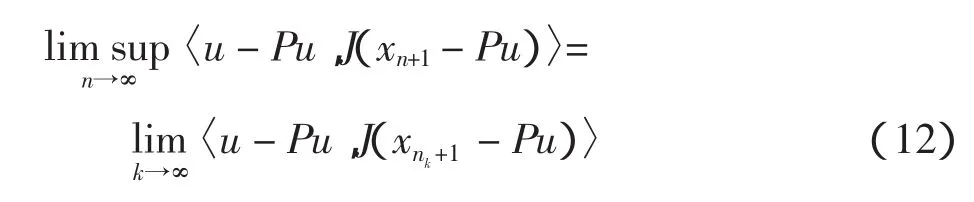
根据Banach空间E的自反性和序列xn的有界性,假设序列xnk⇀x*。由QTx*的紧性可推出存在一个序列zn∈QTx*满足
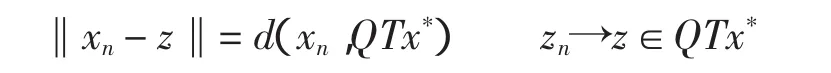
设z≠x*。由具有弱序列连续对偶映射的Banach空间满足 Opoal条件,及式(7)和式(10)可得

这是矛盾的。所以

因为对偶映射J∶E→E*是弱序列连续的对偶映射,根据式(12)、式(13)和引理 5,可得
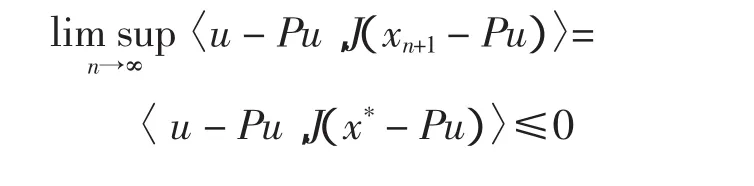
第四步证明
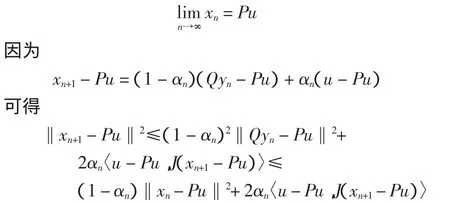
定理3 设E是自反的严格凸Banach空间且E有弱序列连续的对偶映射。C是E中的非空闭凸子集,T∶C→K(E)是非扩张映射。设C是E上太阳非扩张收缩。假设 F(T)≠Ø 满足 T(y)=y,∀y∈F(T),序列 αn满足条件 H1)~H3),则由式(4)定义的序列 xn→Pu,n→∞,其中 P ∶C→F(T)=F(QT)是唯一的太阳非扩张收缩映射。
证明 根据定理2中式(11)中类似的证明,可得
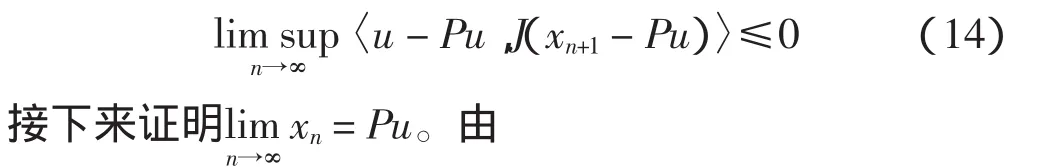
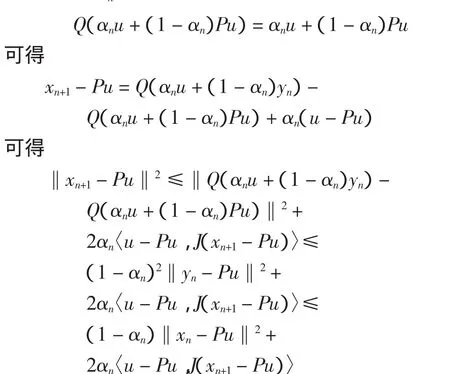
[1]MATSUSHITA S,TAKAHASHI W.Strong convergence theorems for nonexpansive nonself-mappings without boundary conditions[J].Nonlinear Anal,2008,68:412-419.
[2] NADLER S B,JR.Multi-valued contraction mappings[J].Pacific J Math,1969,30:475-487.
[3] SONG Y,CHO Y J.Iterative approximations for multivalued nonexpansive mappings reflexive Banach spaces[J].Math Inequal Appl,2009,12:611-624.
Convergence Theorems for Multivalued Nonexpansive Nonself Mappings
DONG Qiao-li,DENG Bin-chao
(Civil Aviation University of China College of Sciences Tianjin 300300)
Constructing two iterative schemes for mutivalued nonexpansive nonself-mappings and prove strong convergence theorems in a reflexive and strictly convex Banach space.The results generalize and extend the results of Matsushita-Takahashi.
multivalued nonexpansive nonself mapping;reflexive and strictly convex Banach space;weakly sequentially continuous duality mapping
O177.91
A
1674-5590(2010)02-0062-03
2010-05-12;
2010-08-31
中国民航大学科研启动基金项目(08QD10X);中央高校基本科研业务费(ZXH2009D021)
董巧丽(1979—),女,河南濮阳人,讲师,博士,研究方向为偏微分方程数值解.
(责任编辑:杨媛媛)

