基于辛几何构作一类新的带仲裁的认证码
陈尚弟,赵大伟
(中国民航大学理学院,天津 300300)
基于辛几何构作一类新的带仲裁的认证码
陈尚弟,赵大伟
(中国民航大学理学院,天津 300300)
具有仲裁的认证码既要防止敌手的欺骗,又要防止收方和发方的互相欺骗。利用有限域上辛几何构造了一类具有仲裁的认证码,计算了其容量参数。假设编码规则是按照均匀概率分布选择,给出了敌手模仿攻击、敌手替换攻击、发方模仿攻击、收方模仿攻击和收方替换攻击的成功概率。研究结论表明可用辛几何构作许多带仲裁的认证码。
辛几何;带仲裁的认证码;有限域
为解决通信系统中发方与收方互不信任的问题,Simmons引入了具有仲裁认证码的模型,简称为A2-码。在这个模型中有4个参与者:收方、发方、敌手和仲裁。敌手可以对系统进行模仿攻击(I)和替换攻击(S),发方可以进行模仿攻击(T),收方可以进行模仿攻击(R0)和替换攻击(R1),关于这5种攻击的定义见文献[1];将这 5 种攻击成功的概率分别记为 PI、PS、PT、PR0、PR1。仲裁者了解通信系统的全部但不参与通信活动,只有当发方与收方发生争端时才出面解决争端,因此假定仲裁者是诚实的。文献[2-7]利用有限域上典型群的几何空间构造了若干认证码。本文将辛几何用于构造具有仲裁的认证码,并计算了有关参数和各种攻击成功的概率。
1 辛空间
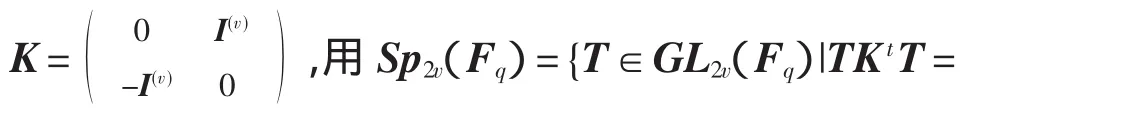
显然,Sp2v(Fq)是GL2v(Fq)的一个子群,则定义Sp2v(Fq)在F(2v)q上的作用如下向量空间联同辛群Sp2v(Fq)在其上的作用称为Fq上2v级辛空间。

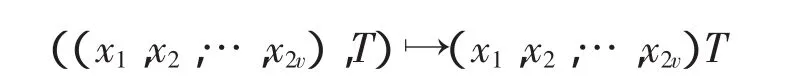
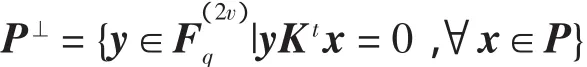
显然,P⊥是的(2v-m)维子空间,称为P的对偶子空间。
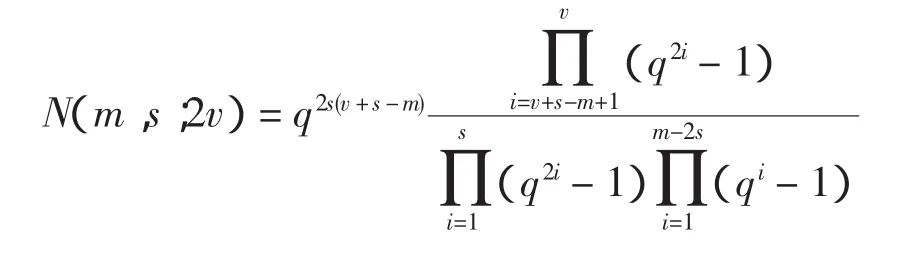
2 构造
设 m1+m2<v,2r<m-m1-m2。设 V1、V2分别为中固定的(m1,0)型、(m2,0)型子空间,V1与 V2正交,并且 V1∩V2=0。取 V=V1⊕V2,则 V 是一个(m1+m2,0)型子空间,而V⊥是一个(2v-m1-m2,v-m1-m2)型子空间。信源集S是所有包含V且含于V⊥的(m,r)型子空间的集合;发方的编码规则集ET是V在V⊥中的补子空间的集合;收方的解码规则集ER是V1在V⊥中的补子空间的集合;信息集M是含于V⊥并且满足与V的和为(m,r)型子空间的所有(m-m1-m2,r)型子空间的集合。对任意 s∈S,m∈M,eT∈ET及 eR∈ER,规定:

首先证明此构作是一个A2-码。
引理 1 1)∀Q∈S 及 eT∈ET,则 Q∩eT=P∈M;
2)∀P∈M,则Q=P+V是相应于P的唯一信源,且存在 eT∈ET,使得 P=Q∩eT。
证明 1)取∀Q∈S,则Q是一个包含V且含于V⊥的(m,r)型子空间。取∀eT∈ET,则 eT是 V 在 V⊥中的补子空间。设P为V在Q中的补子空间,显然P⊂V⊥,则 Q=P⊕V=P⊕V1⊕V2,显然 P=Q∩eT,并且dimP=m-m1-m2,从而

其中PKtP的秩为2r。从而P是一个含于V⊥并且满足与 V 的和为(m,r)型子空间的(m-m1-m2,r)型子空间,即有P∈M是一个信息。
2)设P∈M是一个信息,即P是一个含于V⊥并且与 V 的和为(m,r)型子空间的(m-m1-m2,r)型子空间。令 Q=P⊕V,则 V⊂Q⊂V⊥,并且 Q 是一个(m,r)型子空间,从而Q∈S是一个信源。记Q在V⊥中的补子空间为V3,则V⊥=Q⊕V3=P⊕V⊕V3,令eT=P⊕V3,则eT是V在V⊥中的补子空间,即eT∈ET是一个发方编码规则,并且满足P=Q∩eT。
设Q1是相应于P的另一个信源,则V⊂Q1⊂V⊥并且Q1⊃P,从而Q1⊃P⊕V=Q,又因为dim Q1=dim Q,于是则有Q1=Q,即Q=P+V是相应于P的唯一信源。
因为辛群Sp2v(Fq)可迁的作用在同型子空间的集合上,所以可设
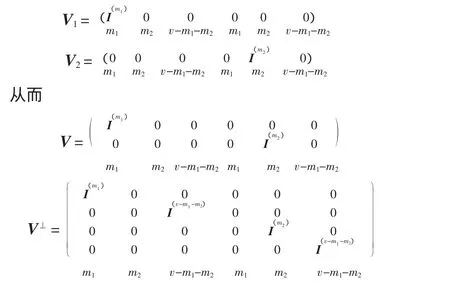
引理2 信源的个数是

证明 因为信源Q是包含V且含于V⊥的(m,r)型子空间,故Q形为
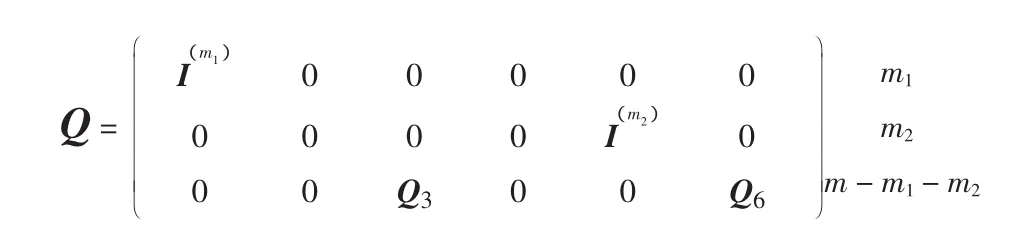
其中(Q3Q6)为2(v-m1-m2)维辛空间中的(m-m1-m2,r)型子空间,从而|S|=N(m-m1-m2,r;2(v-m1-m2))。
引理3 发方编码规则的个数是
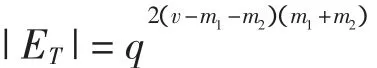
证明 因为任一发方编码规则eT是V在V⊥中的补子空间,从而eT具有如下形式
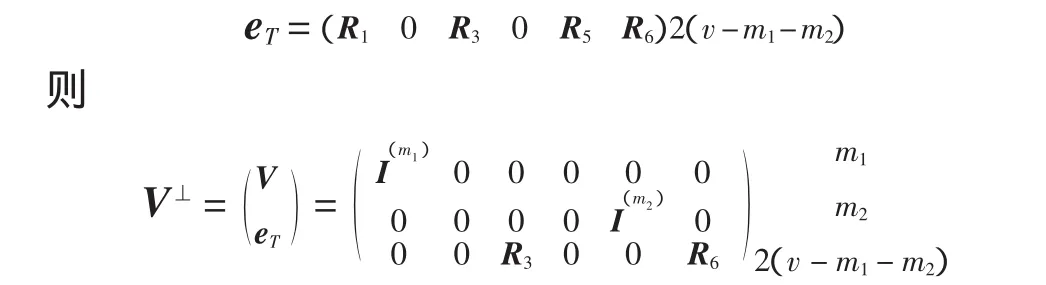
从而(R3R6)为中的2(v-m1-m)2维子空间,只有一个,而 R1、R5任意,所以|ET|=q2(v-m1-m2)(m1+m2)。
引理4 收方解码规则的数量
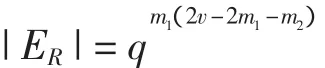
证明 因为任一收方解码规则eR是V1在V⊥中的补子空间,则eR有如下形式

引理5 对∀P∈M,设与P相关联的eT及eR的个数分别为 a、b,则
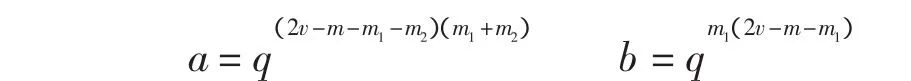
证明 取定P
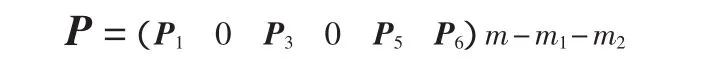
则相应于P的eT有如下形式

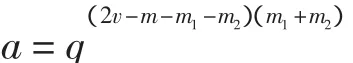
引理6 信息的数量
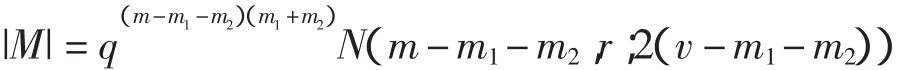
证明 由于对∀P∈M,存在唯一的Q∈S及a个eT∈ET使得 P=Q∩eT。所以引理7 1)∀eT∈ET,与eT相关联的eR的个数为c=qm1m2;
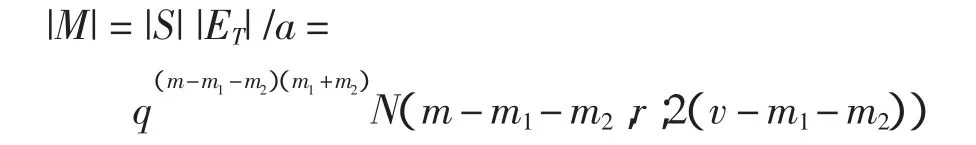
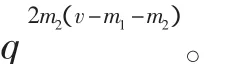
证明 1)取定
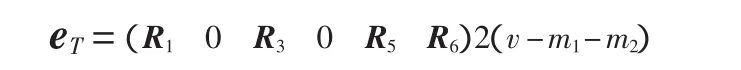
则与eT相关联的eR有如下形式
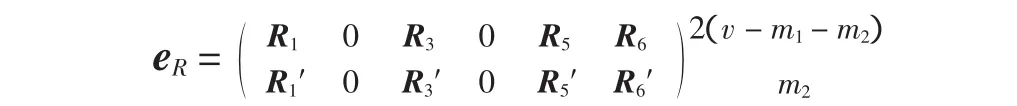
2)取定
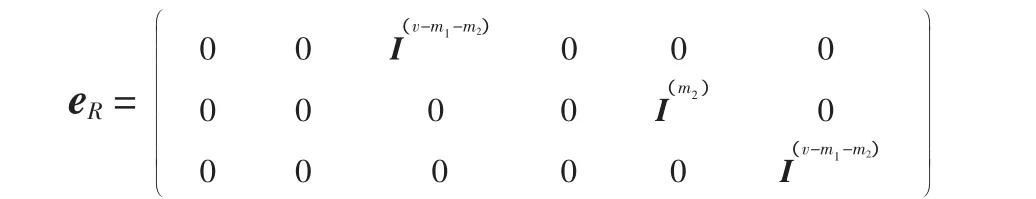
则与eR相关联的eT有如下形式
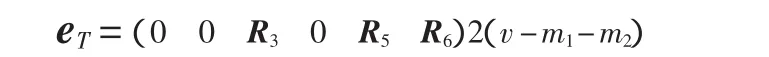
从而可得d=q2m2(v-m1-m2)。
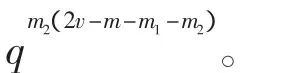
证明 取定 P=(0 0 P30 P5P6)m-m1-m2,与P相关联的eR如引理7中(2)所示,则P中与eR相关联的eT有如下形式
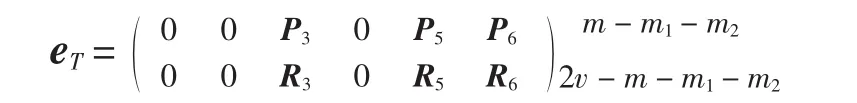

引理9 设P1、P2是共同包含一个发方编码规则eT的两个不同信息,令 k=dim(P1∪P2),则(m-m1-m2+1)≤k≤2(m-m1-m2),并且有
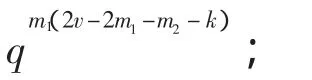

证明 1)由 dimP1=dimP2=m-m1-m2,P1≠P2以及信息的定义可得m-m1-m2+1≤k≤2(m-m1-m2)。(P1∪P2)可表示为
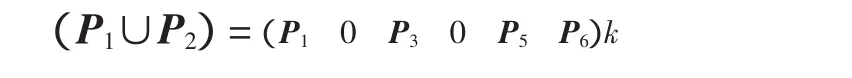
则与(P1∪P2)相关联的 eR可表示为

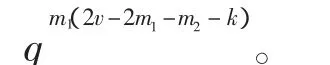
2)取定

则(P1∪P2)包含的与eR相关联的eT形式如下
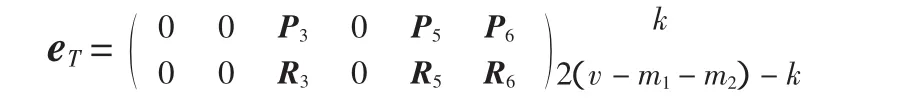
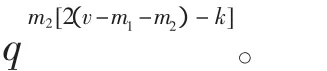
定理1 此构作所得A2-码的参数为

定理2 在此构造所得A2-码中,若编码规则eT及eR都按等概率分布选取,则各种攻击成功的最大概率分别为
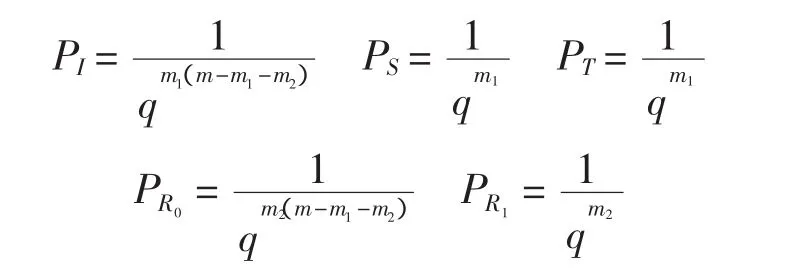
证明 1)设敌方用信息P欺骗收方,模仿攻击成功当且仅当P包含于收方的解码规则,由于包含P的eR的数目为b=qm1(2v-m-m1),故
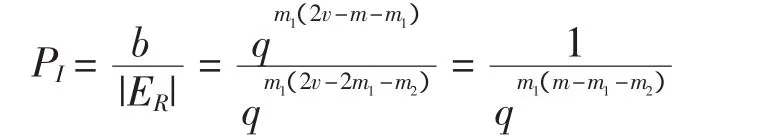
2)设敌方截获发方发送的信息P1并且用P2替换后发给收方,只有当P1包含的信源s1与P2包含的信源s2不同,并且收方把P2当成合法的信息接收,敌方的替换攻击才成功。因为P1⊂eT⊂eR,故敌方的最优策略为选取 eT′⊃P1,使 P2=s2∩eT′,且 dim(P1∪P2)=k尽可能小,则

3)设发方发送一个信息P且P⊄eT,模仿攻击成功当且仅当P⊂eR,因为eR⊃eT,故发方要选取P使包含P的eR尽可能多(eR⊃eT)且P⊄eT,易知这样的eR数最多为qm1(m2-1),而包含eT的eR的个数为c=qm1m2,故
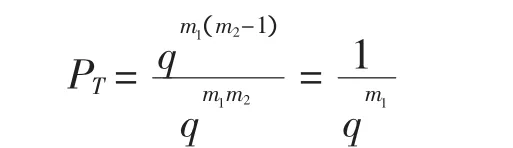
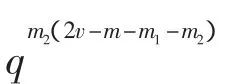

5)设收方收到信息P1后却声称收到P2,只有当P1包含的信源s1与P2包含的信源s2不同,并且P2可以由发方的编码规则加密得到,收方的替换攻击才成功。由于 P1⊂eT⊂eR,故收方的最优策略为选取eT′满足P1⊂eT′⊂eR,使 P2=s2∩eT′,且 dim(P1∪P2)=k 尽可能小,故

[1] SIMMONS G J.Message Authentication with Arbitration of Transmitter/Receiver Disputes[C]//Proc Eurocrypt′87,Berlin:Springer Verlag,1988:151-165.
[2]GAO YOU,SHI XINHUA,WANG HONGLI.Construction of authentication codes with arbitration from singular sympleetic geometry over finite fields[J].Acta Scientiarum Naturalium Universitatis Nankaiensis,2008(6):72-77.
[3] 马文平,王新梅.基于伪辛几何的具有仲裁的认证码的构造[J].应用数学学报,2000,18(4):294-297.
[4] 马文平,王新梅.基于酉几何的等概的具有仲裁的认证码的构造[J].应用数学学报,2001,24(2):271-276.
[5] 李志慧,李瑞虎.利用伪辛几何构作带仲裁的认证码[J].兰州大学学报(自然科学版),2005,41(5):123-126.
[6]高 有,陶亚媛.利用有限域上交错矩阵构造Cartesian认证码[J].高校应用数学学报,2007,22A(4):385-390.
[7] 王红丽,高 有.利用奇异伪辛几何构作具有仲裁的认证码[J].河北理工大学学报(自然科学版),2008(2):65-70.
Construction of Authentication Codes with Arbitration over Symplectic Geometry
CHEN Shang-di,ZHAO Da-wei
(College of Science,CAUC,Tianjin 300300,China)
Unconditionally secure authentication codes with arbitration protects against deceptions from the transmitter and from receives as well as those from the opponent.This paper describes a new construction of authentication codes with arbitration using symplectic geometry over finite fields,and their size parameters are computed.Assuming that the encoding rules one chosen according to a uniform probability distribution,the probabilities of a successful impersonation by the opponent, a successful substitution by the opponent, a successful impersonation by the transmitter,a successful impersonation by the receiver and a successful substitution by the receiver.This illustrates many authentication codes with arbitration can be constructed from symplectic geometry.
symplectic geometry; authentication codes with arbitration; finite field
O157.4
A
1674-5590(2011)02-0051-04
2010-04-21;
2010-07-19
天津市自然科学基金项目(08JGYBJG13900);中国民航大学科研项目(09CAUC-S02)
陈尚第(1964—),男,山西应县人,教授,博士,研究方向为代数图论、密码和编码.
(责任编辑:杨媛媛)

