基于Lyapunov函数的不确定模糊控制系统设计
巩长忠,王 灿
(中国民航大学理学院,天津 300300)
基于Lyapunov函数的不确定模糊控制系统设计
巩长忠,王 灿
(中国民航大学理学院,天津 300300)
研究一类不确定T-S模糊系统的稳定性问题,考虑了平行与非平行分配补偿控制器的设计,并把线性矩阵不等式方法运用到了非平行分配补偿控制器中。基于Lyapunov函数把系统稳定的充分条件延伸到了不确定模糊控制系统。最后通过数值实例说明了本结论的有效性。
参数不确定;T-S模糊系统;Lyapunov函数;平行分配补偿器;非平行分配补偿器;线性矩阵不等式
T-S模糊系统近年来得到广泛研究,已成为处理非线性控制问题有效方法。对参数不确定T-S模糊系统的研究,已取得不少有价值的理论成果。文献[1-3]研究了不确定模糊系统的稳定性问题。文献[4]中给出了一些T-S模糊系统稳定性的条件。文献[5-7]中对离散和连续模糊系统提出了非平行非线性分配补偿器。
文献[8]通过模糊Lypunov函数方法,对模糊控制系统的稳定进行了研究,给出了系统稳定的充分条件。但并没有考虑参数不确定性。在此基础上,本文研究了参数不确定T-S模糊系统,通过线性矩阵不等式方法得到不确定系统稳定的充分条件并把线性矩阵不等式方法运用到了非平行分配补偿器中。
1 基于T-S模型的不确定模糊控制系统
在本文中,考虑如下T-S模糊控制系统
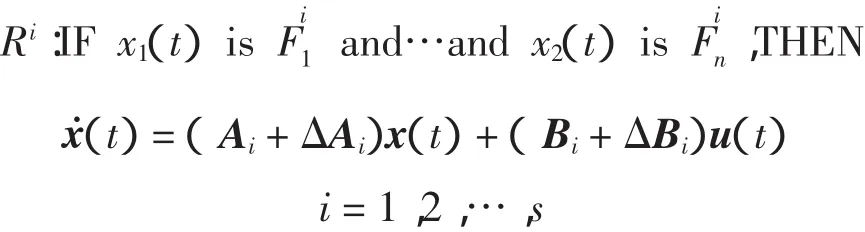
其中:x(t)=[x1,…,x(nt)]∈Rn是状态向量;u(t)∈Rm是系统的控制输入;,…是模糊集合;Ai∈Rn×n,Bi∈Rn×m分别是系统矩阵和输入矩阵;ΔAi、ΔBi是适当维数的时变矩阵,其在系统模型中表示参数不确定性;s是模糊模型的规则数。
应用单点模糊化、乘积推理和中心加权反模糊化推理方法,得全局模糊系统模型
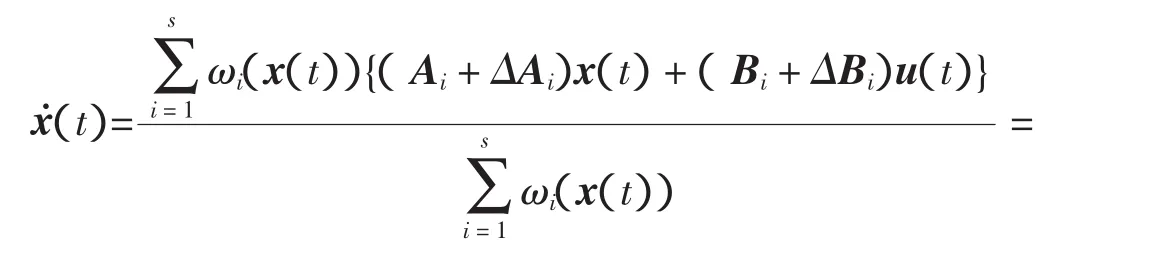
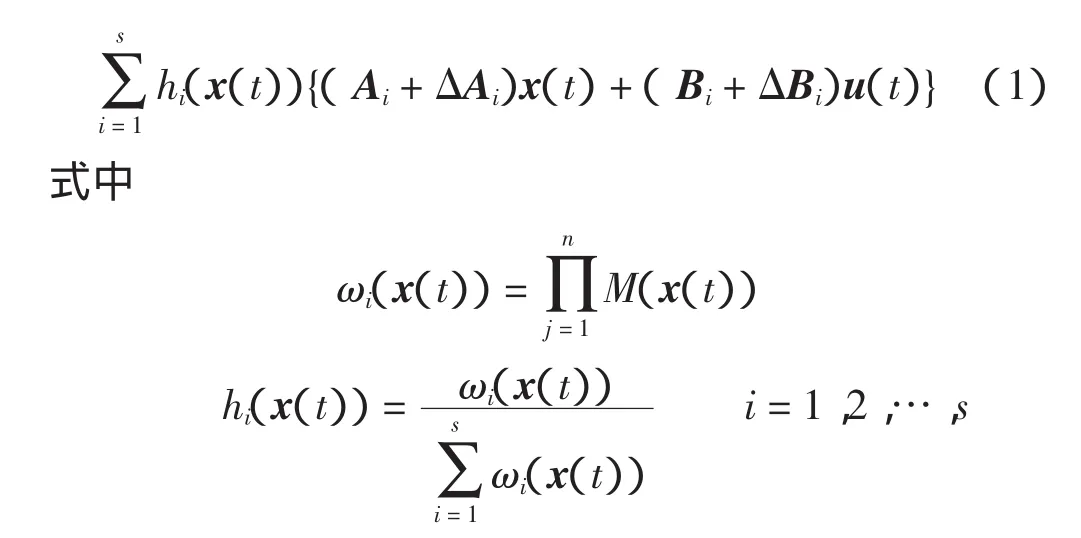
并且有以下基本性质
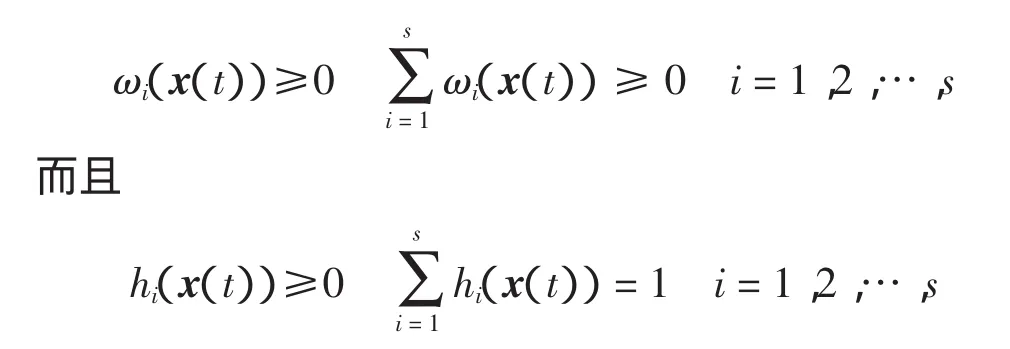
式(1)可写为如下形式

为了简单方便,在x(t)和hi(x(t))中省略了t。
假设 假设参数不确定性矩阵是范数有界的,其形式为

式中:Di、E1i和E2i是已知的适当维数矩阵;Fi(t)是未知的函数矩阵,其每个元素是可测的函数,并且满足FTi(t)Fi(t)≤I,这里I是单位阵。
引理1 对具有适当维数的常数矩阵D、E及对称常数矩阵S,矩阵不等式
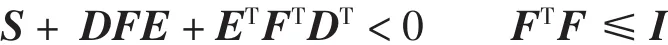
成立的充分必要条件是:存在ε>0,满足下面的矩阵不等式[9]
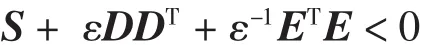
引理2 已知对称矩阵W∈Rn×n及矩阵B∈Rn×n,如果存在常量 α >0,矩阵 L∈Rn×n,U∈Rn×n,和正定矩阵 P∈Rn×n,J∈Rn×n使得线性矩阵不等式

成立,则U是非奇异的,并且K=αLU-1满足如下的非线性矩阵不等式[10]
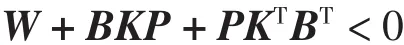
“*”表示对称位置的转置矩阵。
2 主要结论
在此部分中,将分析系统⑴的稳定性和控制器的设计。
1)稳定性分析和平行分配补偿控制器设计
考虑如下平行分配控制器
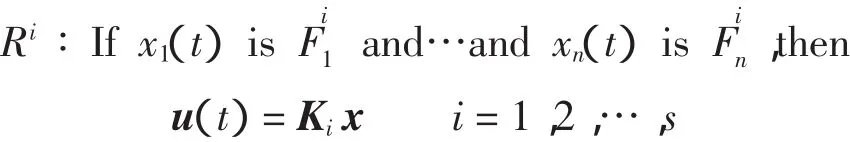
全局模糊控制器为
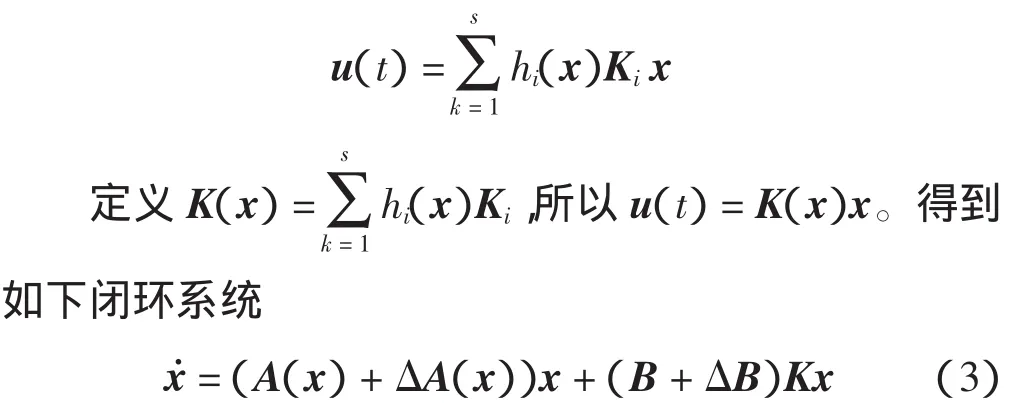
定理1 如果控制增益参数矩阵{Ki}si=1给出,存在 PT=P>0,ε1>0,ε2>0,使得
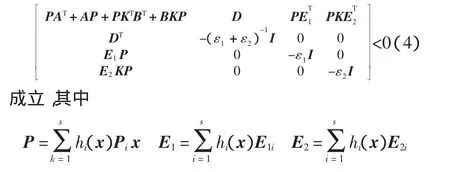
则式(3)渐近稳定。
证明 考虑如下函数:V(x)=xTP-1x。对V沿系统(3)求导,可得
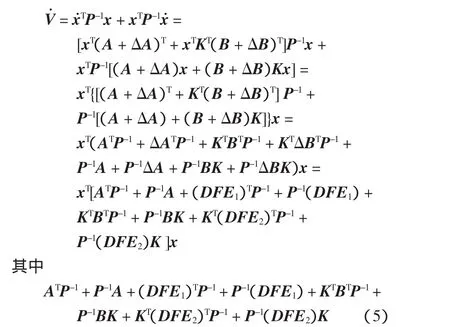
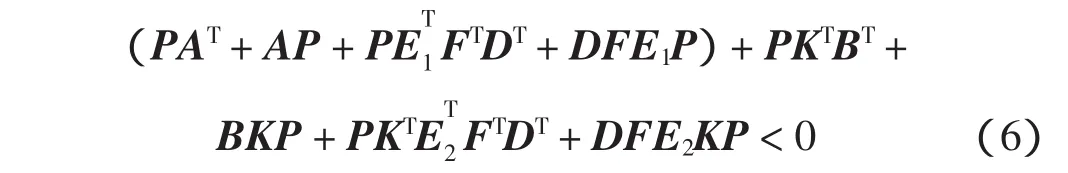
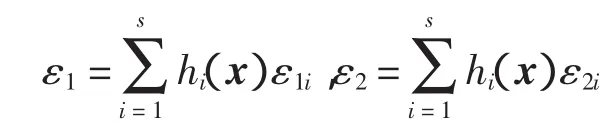

利用Schur补得到式(4)。所以系统(3)渐近稳定。

成立,则系统(3)渐近稳定。
证明
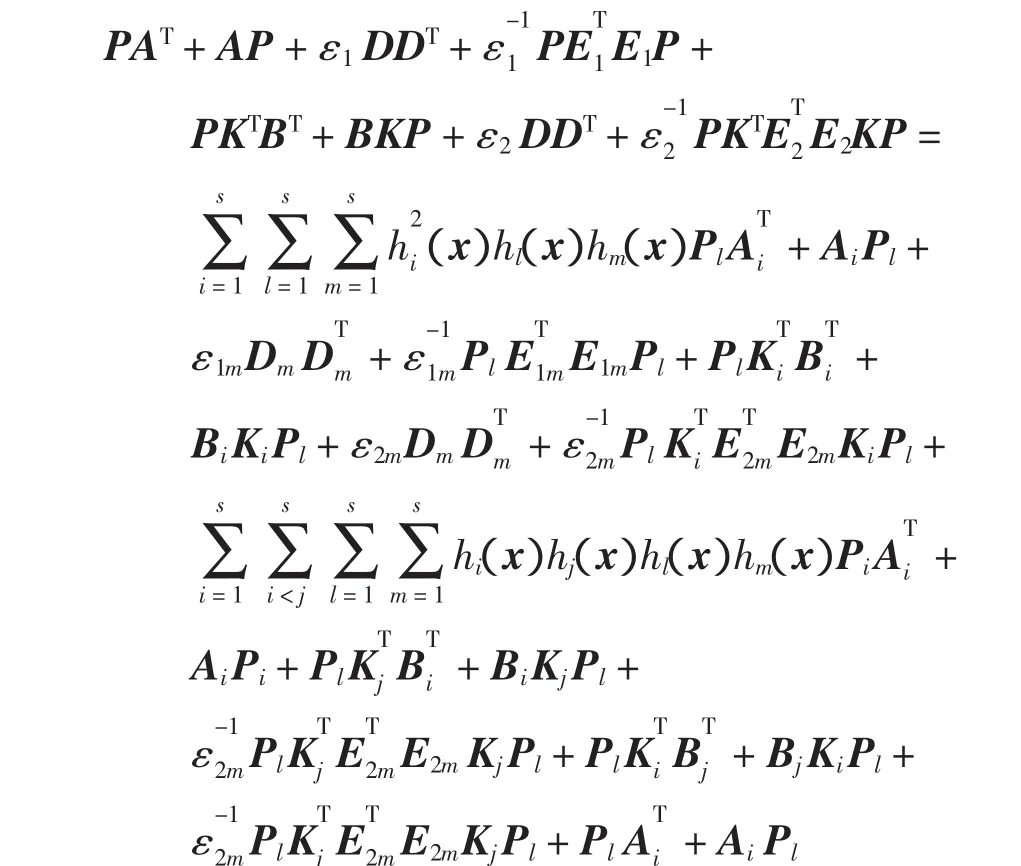
由式(7)、式(8)可得式(4)成立,再由定理 1得系统(3)渐近稳定。
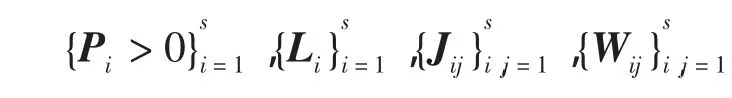
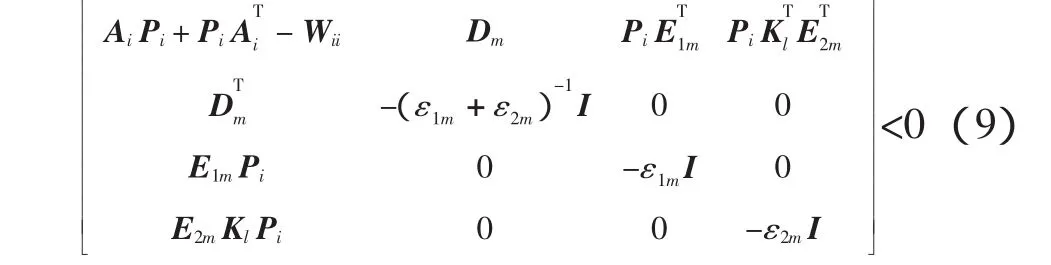

则有系统(3)渐近稳定。其中“*”表示对称位置的转置矩阵。
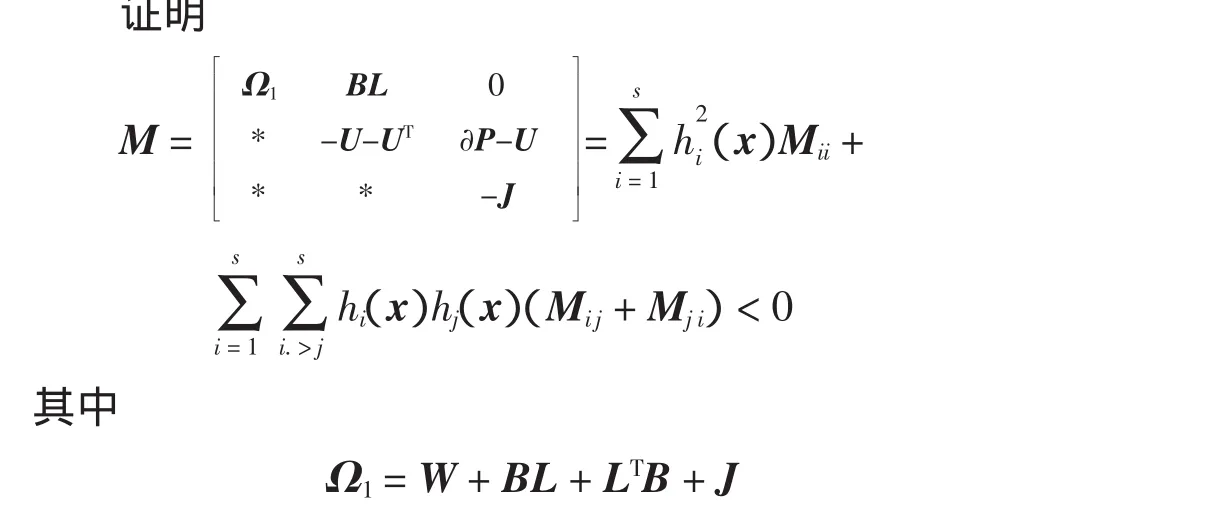
由引理2,可知
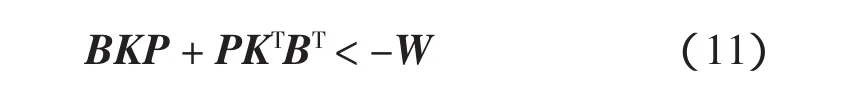
其中
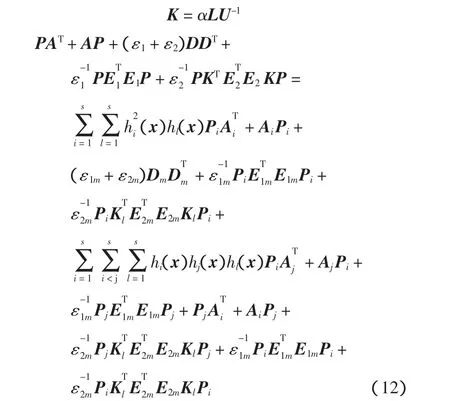
由式(9)和式(10),得到式(12)小于
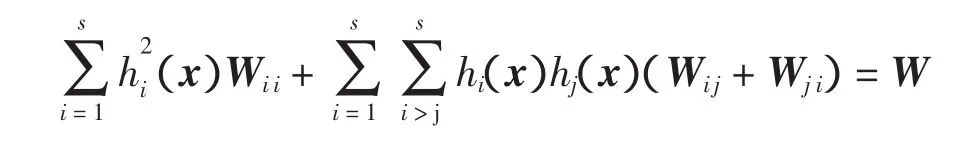
式(11)、式(12)联立得式(4)。由定理 1可知系统(3)渐近稳定。
2)非平行分配补偿控制器设计
考虑在文献[9]中提到的非平行分配补偿控制器
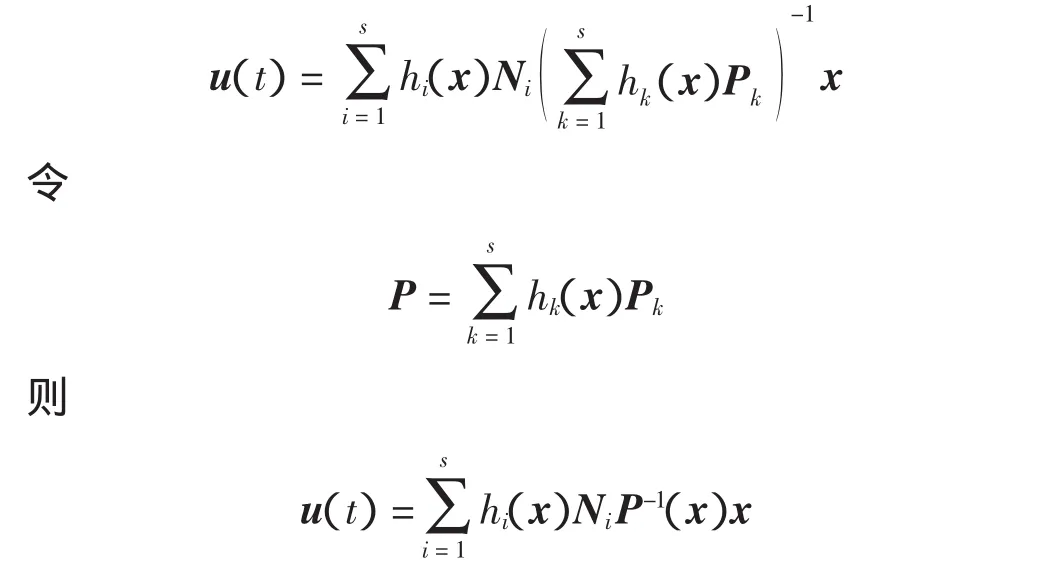
得到如下闭环系统
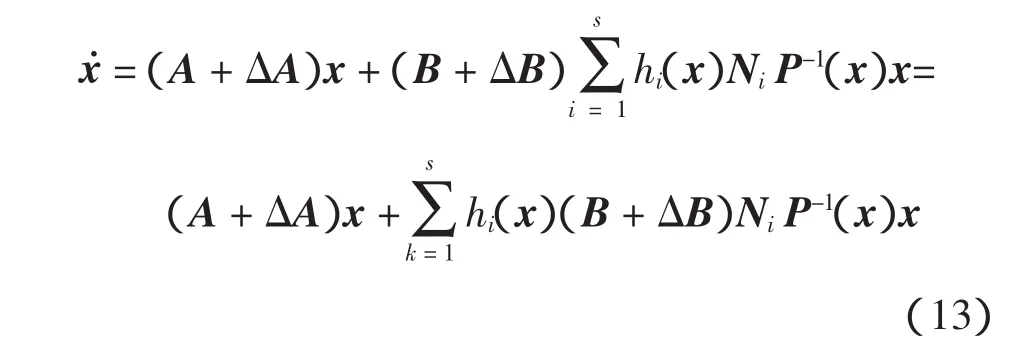
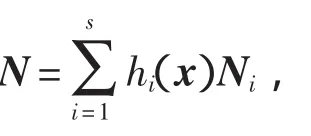
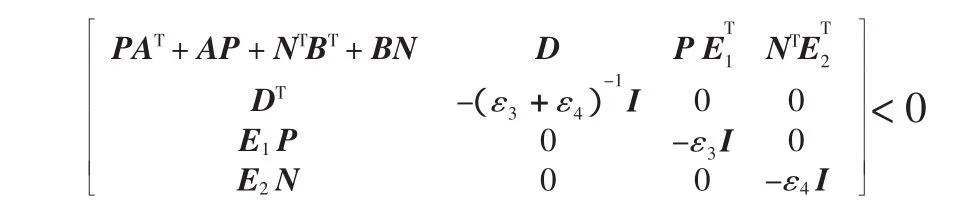
则系统(13)渐近稳定。


若式(14)<0,则由引理1可得:存在常数ε3>0,ε4>0,使得
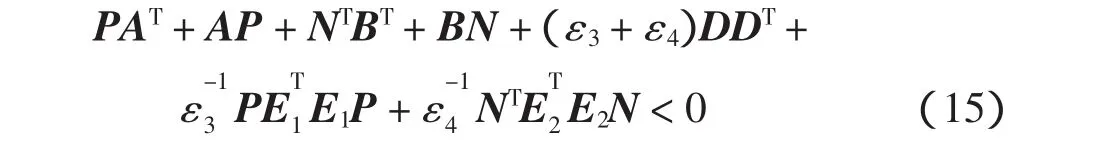
由 Shur补,式(15)可写为

若式(16)成立,则系统(13)渐近稳定。
3 数值算例
假设具有如下系统:
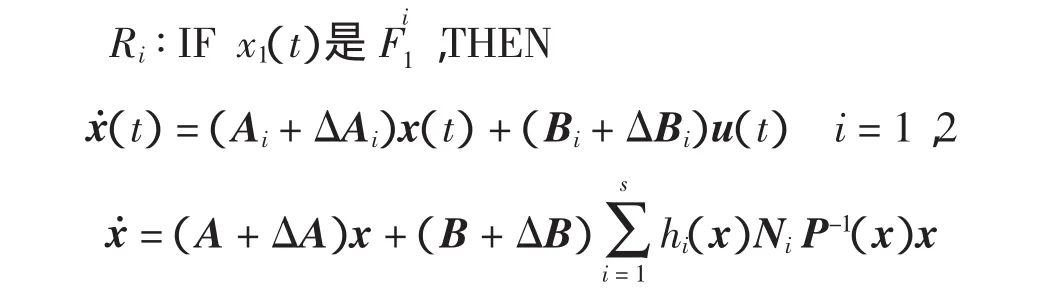
考虑系统(13),其中
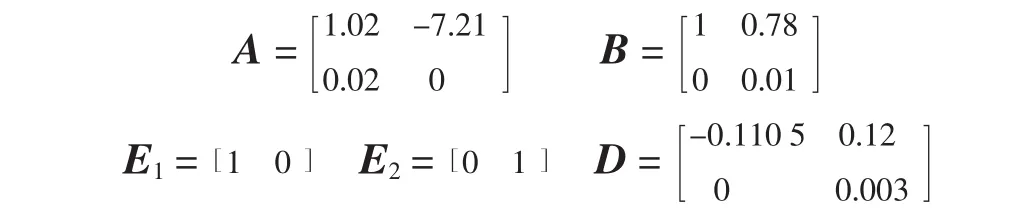
代入定理4中的式(16)可得到
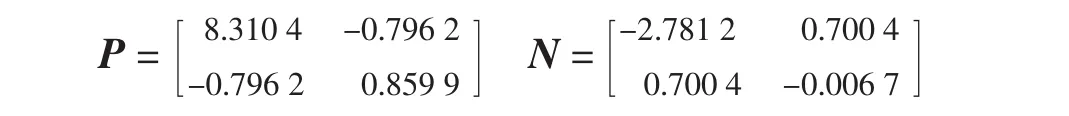
通过解LMIS可得到P、N。根据定理4可知由非平行分配控制器得到的闭环系统渐进稳定。
[1]ZHOU SHAOSHENG,FENG GANG,FENG CHUN-BO.Robust control for a class of uncertain nonlinear systems:adaptive fuzzy approach based on backstepping[J].Fuzzy Sets and Systems,2005,151(1):95-98.
[2] VU N PHAT.Robust stability and stabilizability of uncertain linear hybrid systems with state delays[J].IEEE Trans,2005,52(2):94-98.
[3] HAN HO CHOI.Robust stabilization of uncertain fuzzy systems using variable structure system approach[J].IEEE Transactions on Fuzzy Systems,2008,16(3):715-724.
[4]WANG H O,TANAKA K,GRIFFIN M F.An approach to fuzzy control of nonlinear systems:Stability and design issues[J].IEEE Trans Fuzzy Syst,1996,4(1):14-23.
[5]GUERRA T M ,VERMEIREN L.LMI-based relaxed nonquadratic stabilization conditions for nonlinear systems in the Takagi-Sugeno's form[J].Automatica,2004,40(5):823-829.
[6] LAM H K,LEUNGM F H F.LMI-based stability and performance conditions for continuous-time nonlinear systems in Takagi-Sugeno's form[J].IEEE Trans Syst Man Cybern,2007,37(5):1396-1406.
[7]TANAKA K,HORI T,WANG H O.A descriptor system approach to fuzzy control system design via fuzzy Lyapunov functions[J].IEEE Trans Fuzzu Syst,2007,15(3):333-341.
[8] LI J,ZHOU S,XU S.Fuzzy control system design via fuzzy Lyapunov functions[J].IEEE Trans Fuzzu Syst,2008,38(6):1657-1661.
[9] 俞 立.不确定离散线性系统的最优保成本控制[J].控制理论与应用,1999,16(5):639-642.
[10]GEROMEL J C,KOROGUI R H.Analysis and synthesis of robust control systems using linear parameter dependent Lyapunov functions[J].IEEE Trans Autom Control,2006,51(12):1984-1989.
Uncertain Fuzzy Control System Design via Lyapunov Functions
GONG Chang-zhong,WANG Can
(Science College, CAUC, Tianjin 300300, China)
This correspondence deals with the problems of analysis and design for a class of uncertain continuous-time Tskagi-Sugeno fuzzy control systems.Both parallel and nonparallel distributed compensation controllers are considered.An LMI technique will be extended to a non-PDC approach.Sufficient conditions for the stability of fuzzy control systems are extended to uncertain continuous-time Tskagi-Sugeno fuzzy control systems that based on a fuzzy Lyapunov function.The effectiveness of the proposed approaches is shown through a numerical example.
uncertain continuous-time; Tskagi-Sugeno fuzzy control systems; Lyapunov function; PDC approach; non-PDC approach;LMI
TP202
A
1674-5590(2010)02-0055-04
2010-05-12;
2010-07-11
巩长忠(1959—),男,山东蓬莱人,教授,博士,研究方向为非线性控制与模糊控制.
book=61,ebook=88
(责任编辑:杨媛媛)

