基底完全粗糙时太沙基地基承载力系数的解析解

程国勇，邱 睿，段 淳

（中国民航大学机场学院，天津 300300）

基底完全粗糙时太沙基地基承载力系数的解析解

程国勇，邱 睿，段 淳

（中国民航大学机场学院，天津 300300）

当前普遍采用的太沙基极限承载力公式中并未给出承载力系数Nγ的解析形式，而且Nc的表达方式在不同资料中不统一。针对以上情况，根据地基土的极限平衡原理，研究得出了条形基础底面完全粗糙条件下太沙基极限承载力系数Nγ′、Nc′的解析解。然后计算得出太沙基极限承载力系数的曲线以供查用。以上成果可为太沙基地基极限承载力公式的应用及研究工作提供参考。

太沙基公式；地基极限承载力；极限平衡原理；解析解

地基极限承载力是土力学研究的一个经典课题，其中太沙基（K.Terzaghi）理论是基于极限平衡理论确定条形地基极限承载力的重要方法。在该理论中考虑了地基土的自重，基于以下三条假定[1-2]：

1）基础底面完全粗糙；

2）基底以上两侧土体当作均布荷载（不考虑基底以上两侧土体的抗剪强度影响）；

3）地基中滑动土体分为三角形压密区（弹性核）、朗肯被动区以及对数螺旋线过渡区。

太沙基地基极限承载力的理论公式为

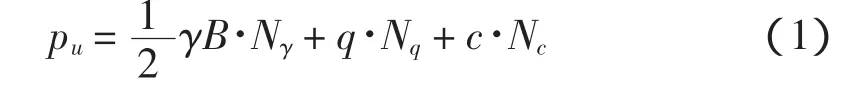
其中：Nγ、Nq、Nc为太沙基地基承载力系数。

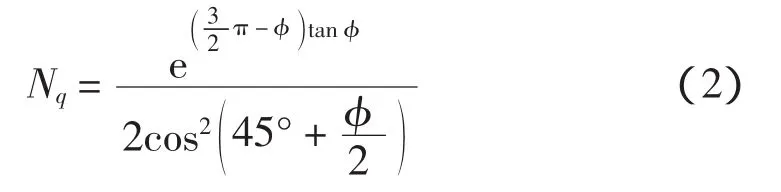
在上述公式中，一般的土力学著作或教材仅给出Nq及Nc的解析公式，对于承载力系数Nγ仅用曲线的形式给出，具体过程一般不给出；在实际应用中存在计算图示不严谨或与假定条件不能完全对应；此外目前采用的太沙基地基承载力系数Nc仍借用了普朗特尔（L.Prandtl）地基极限承载力的结论，即：Nc=（Nq-1）cot φ，而由于两种方法采用的计算模型不同，Nc与Nq之间并无此关系。以上这些问题的含糊其辞给地基承载力理论的学习及研究带来困难[3-5]。

本文根据极限平衡原理对这一经典的土力学问题进行了研究，得出基础底面完全粗糙情况下太沙基地基承载力系数Nγ的解析式，且经过详细推导得到承载力系数Nc的表达式。然后给出基础底面完全粗糙情况下太沙基地基承载力系数的曲线。希望通过本文工作为太沙基地基极限承载力公式的学习、应用及研究工作提供参考。

1 基底完全粗糙时太沙基承载力系数解析解

仍采用太沙基理论的上述3条假定。此时弹性核与两侧面与水平面夹角α=φ。计算图示如图1所示。地基破坏时沿 bde和 bd′e′滑动，bd和 bd′是对数螺线，方程为 r=r0·exp（θ·tan φ）。de 和 d′e′是直线，与水平面的夹角等于 45°- φ/2，即 ade及 ad′e′区为朗肯被动区。从图1中可以看出

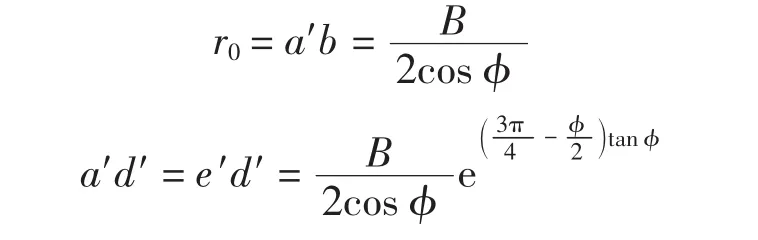
取弹性核为隔离体，根据几何条件可知此时被动土压力Ep必定竖直向上，如图2所示。其中：γ、c分别为基底下土体的重度（kN/m3）及黏聚力（kPa）；B 为基础底面宽度（m）；q为基底以上土体荷载（kPa），q= γ0D，γ0为基底以上土体的加权平均重度，D为基础埋深。

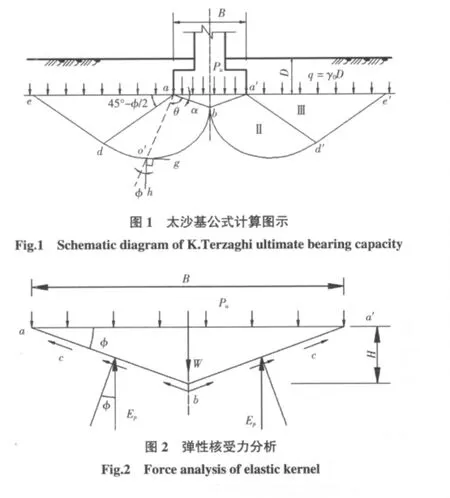
根据静力平衡条件可得

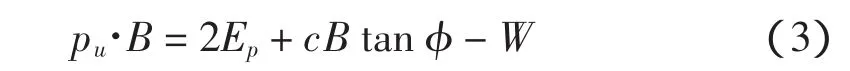
可见，只要求出了作用于刚性核侧面的被动土压力Ep，则地基的极限承载力就可确定。将刚性核的ab及a′b边看作挡土墙的墙背，计算以下3种特殊条件下的被动土压力Ep。

1）q=0、c=0、γ ＞ 0，即仅由地基土重产生的被动土压力Ep1。

根据对a′点的力矩平衡计算Ep1，分别计算朗肯被动区a′d′e′、对数螺旋线区重力、对数螺旋线破坏面下反力以及d′e′上合力对于a′点力矩（顺时针为正）。

a）朗肯被动区 a′d′e′重力对于 a′点力矩 Mr1

三角形 a′d′e′重量为

对于a′点力矩为

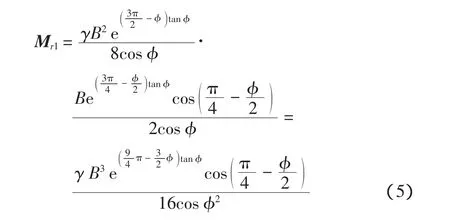
b）对数螺旋线区重力对于a′点力矩Mr2

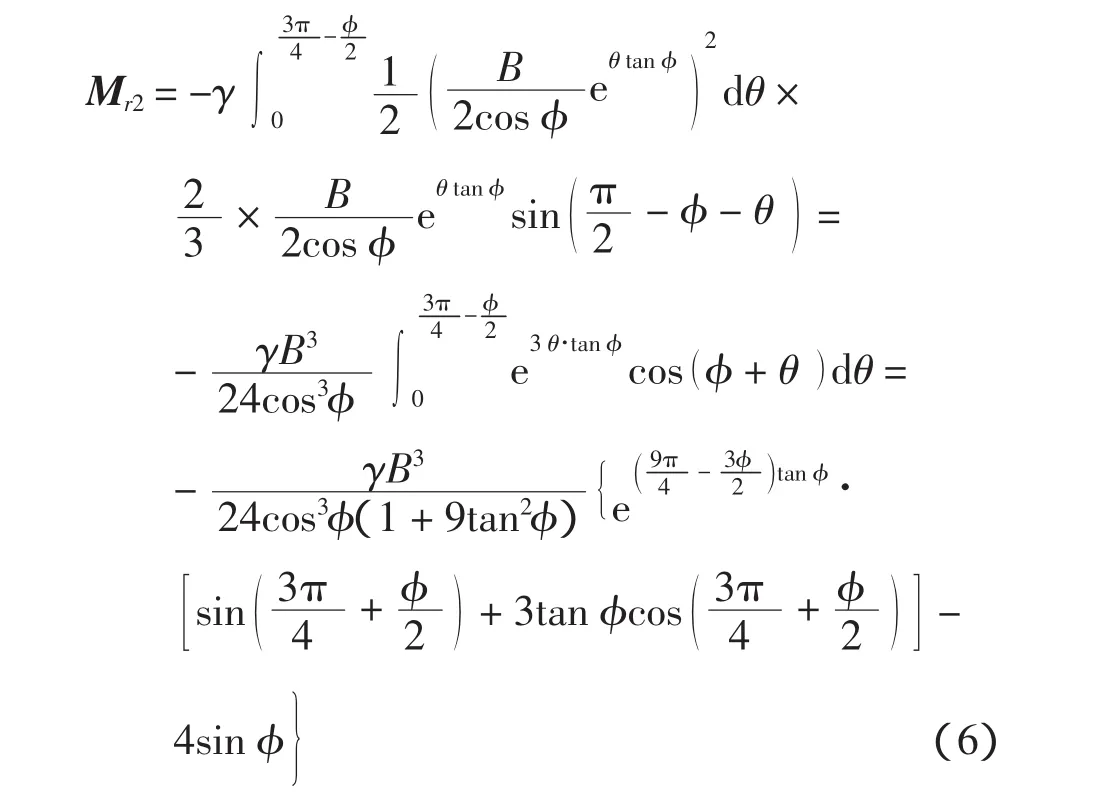
c）对数螺旋线破坏面下反力对于a′点力矩Mr3

根据对数螺旋线性质，当处于极限平衡状态时，对数螺旋线破坏面上合力通过a′点，因此对数螺旋线破坏面下反力对a′点力矩Mr3=0。

d）d′e′上合力对于 a′点力矩 Mr4

由于a′d′e′为朗肯被动区，竖向应力为小主应力，破坏面 d′e′上在 d′点的法向应力为

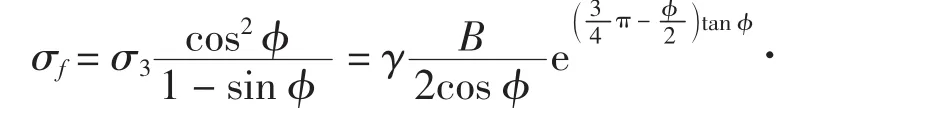
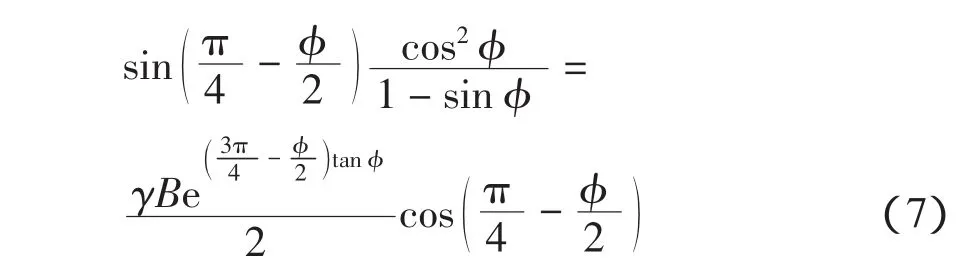
在 d′点 d′e′面上的切应力

d′e′面上合力 R 为

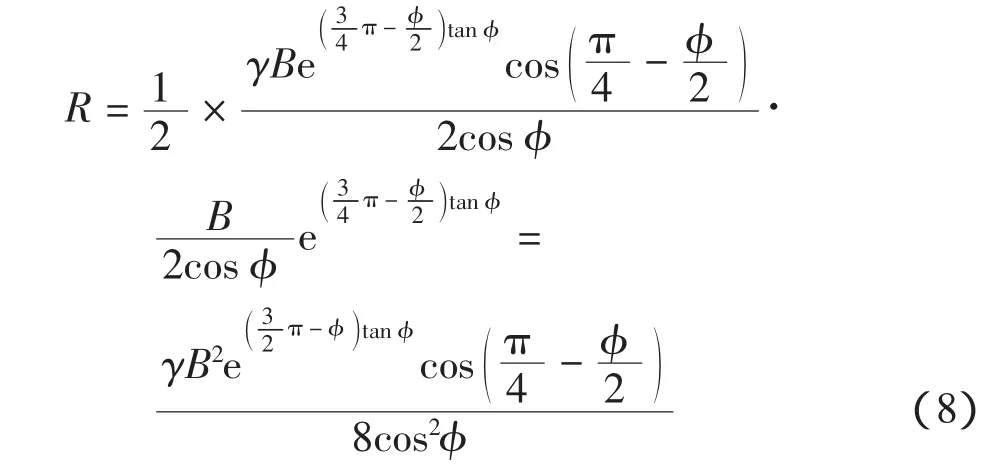
R方向与d′e′面法线成φ角，R对与a′点的力臂如图3所示。

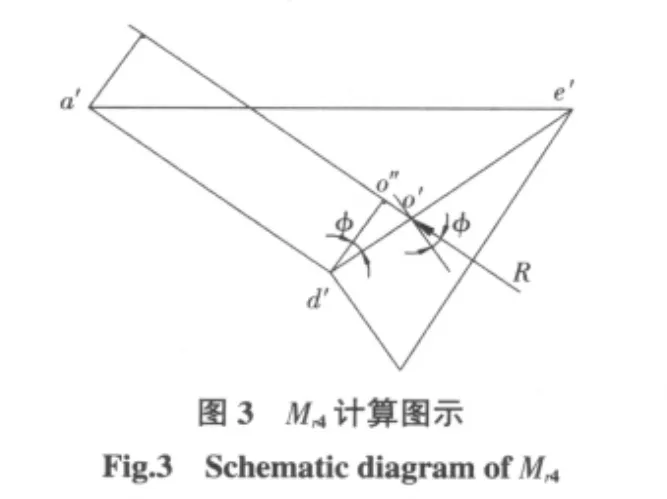
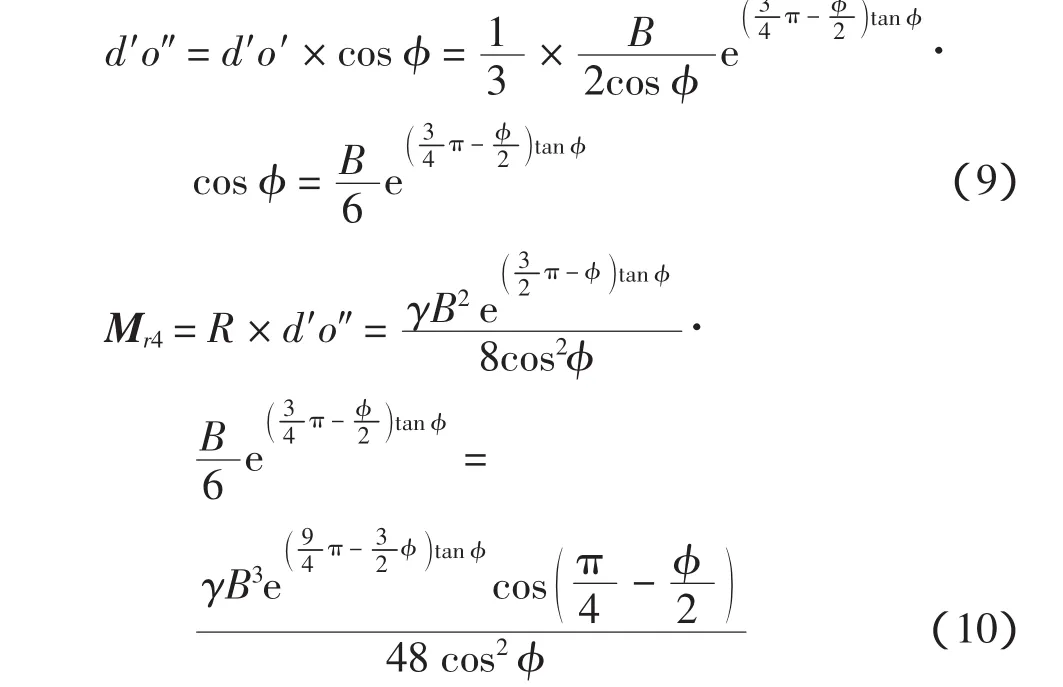
根据对a′点的力矩平衡

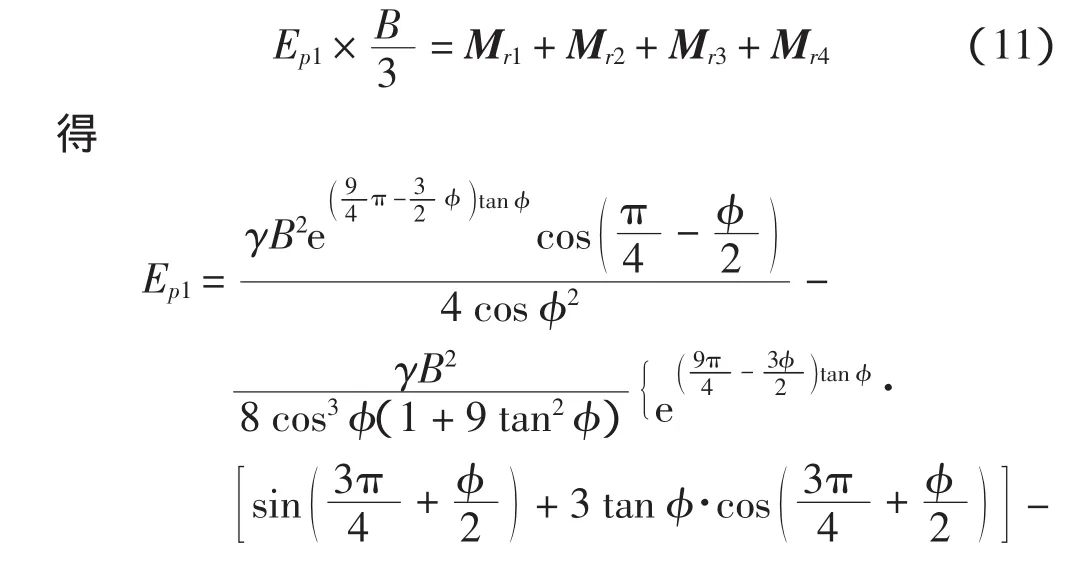
2）q＞ 0、c=0、γ =0，即仅由两侧超载 q 产生被动土压力Ep2。

根据被动土压力理论，由于基础两侧超载产生的被动土压力在ab及a′b滑动面上呈矩形分布，根据对a′点力矩平衡

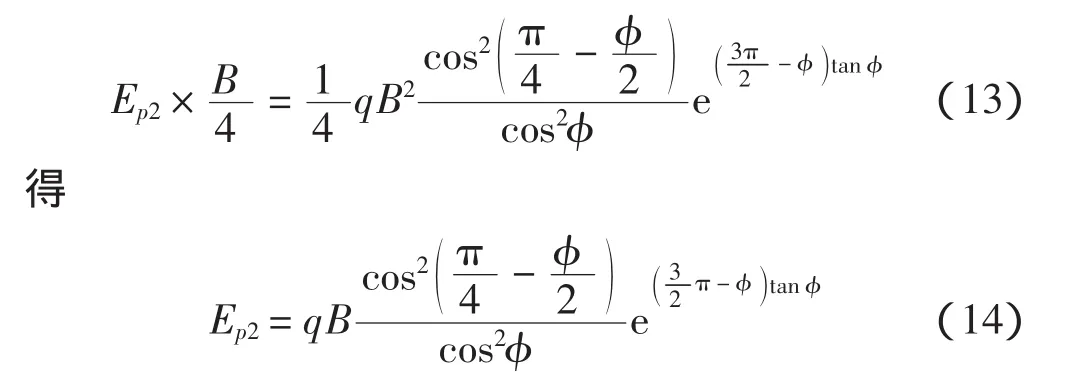
3）q=0、c＞ 0、γ =0，即仅由黏聚力 c产生的被动土压力Ep3。

根据被动土压力理论，土的粘聚力在ab及a′b滑动面上产生的被动土压力呈矩形分布，Ep3对于a′点力臂为B/4。

根据对数螺旋线性质，对数螺旋线（任意点的切线与矢径夹角为π/2+φ，对数螺旋线上粘聚力c对于 a′点力矩为

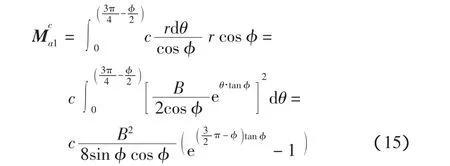
b）d′e′面上粘聚力 c 对于 a′点的力矩

d′e′面上粘聚力合力力臂 a′o‴，如图 4 所示。

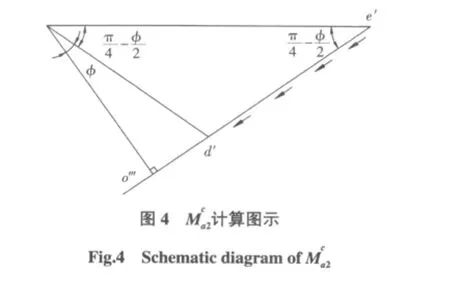
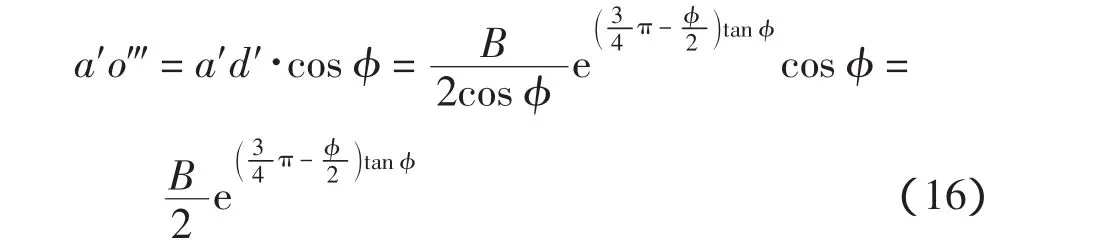
d′e′面上粘聚力对于 a′点的力矩为

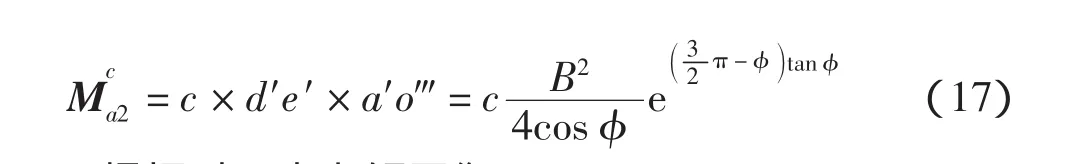
根据对a′点力矩平衡

得由黏聚力c产生的被动土压力Ep3为

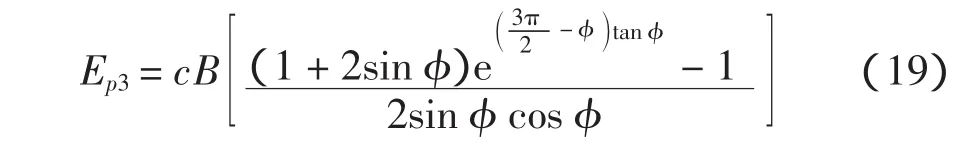
根据叠加原理，总的被动土压力Ep就等于3种情况下被动土压力的总和，即

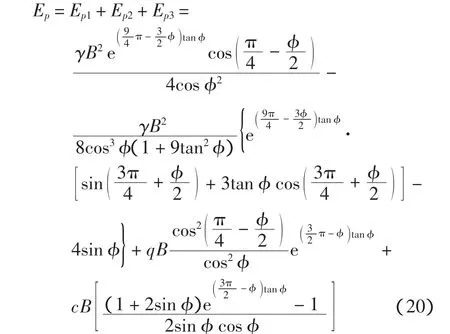
将式（20）代入式（3）得

根据式（1），得

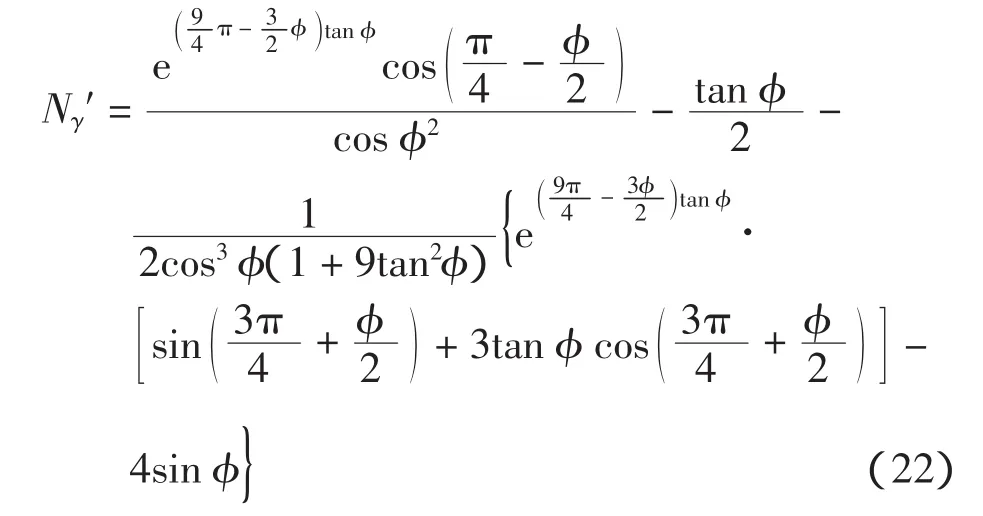
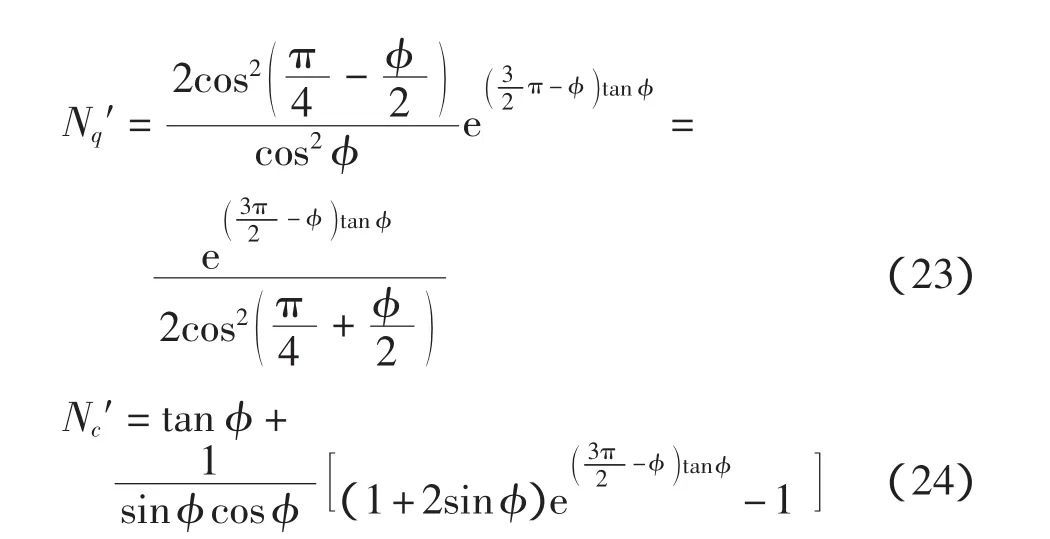
当φ→0时，根据罗彼塔法则，limφ→0Nc=6.71。

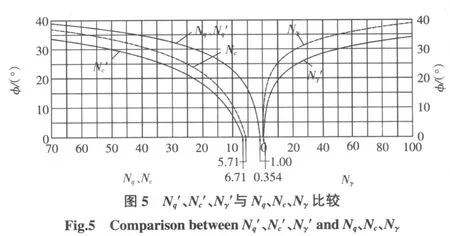
可见在基底完全粗糙情况下，能得到3个承载力系数的解析表达式，与式（2）比较，Nq′与现有系数Nq完全相同，Nc则不同。根据本文推导式计算太沙基承载力系数 Nq′、Nc′、Nγ′，与现有系数 Nq、Nc、Nγ的比较如图5所示。

2 结语

通过以上研究，得到以下结论供学习及研究人员借鉴：

1）根据极限平衡原理推导得出太沙基承载力系数Nγ的解析式。

2）由于采用的计算模型不同，太沙基地基承载力系数Nc不能借用普朗特尔理论的结果。

3）目前普遍采用的太沙基地基承载力系数中，Nq是正确的，其余两个存在较大误差。

[1] 陈仲颐，周景星，王洪瑾.土力学[M].北京：清华大学出版社，1994.

[2] 王 哲，王国才，陈 禹，等.矩形浅基础地基极限承载力的理论解[J].岩土力学，2008，29（4）：1001-1004.

[3] 商建林，涂长红，谢叶彩.地基极限承载力确定方法的分析与评价[J].西部探矿工程，2007（2）：140-142.

[4]杜世回.理解和应用地基承载力的若干问题[J].铁道勘查，2007（3）：95-97.

[5]易永利.复合地基承载力的影响因素和确定方法[J].岩土工程界，2009，12（8）：25-28.

Analytical Formula of K.Terzaghi Ultimate Bearing Capacity Coefficient Under Totally Coarse Foundation Base

CHENG Guo-yong， QIU Rui， DUAN Chun
（The Airport College， CAUC， Tianjin 300300， China）

In the K.Terzaghi ultimate bearing capacity formula，the coefficient Nγhas not been given in a definite expression and the factor of Ncis different in different material.To solve this problem，according to the ultimate balance theory，the analytical formula of Nγand Ncare derived and the correctness of the factor Ngis proved for the strip foundation with absolute coarse base.At last，the curves of all the factor in K.Terzaghi ultimate bearing capacity are provided，which is valuable for the application and research of the K.Terzaghi ultimate bearing capacity theory.

K.Terzaghi formula； K.Terzaghi ultimate bearing capacity； ultimate balance theory；analytical formula

TU4

A

1674－5590（2011）01－0025－04

2010-06-25；

2010-11-19 基金项目：中国民航大学科研启动项目（k24028）

程国勇（1971—），男，河北衡水人，副教授，博士，研究方向为地基基础检测技术与加固理论.

（责任编辑：杨媛媛）