基于小波分析的机场道面平整度细节研究
王 维,胡春飞
(中国民航大学机场学院,天津 300300)
基于小波分析的机场道面平整度细节研究
王 维,胡春飞
(中国民航大学机场学院,天津 300300)
采用小波理论对机场刚性跑道平整度进行分析。针对某机场道面,采用Matlab对其纵断面信号进行小波变换分解 ,得到不同高频下机场刚性道面纵断面长波和短波的具体波动幅度和位置,可作为国际平整度IRI的一种补充,为航空器-机场道面相互作用动力学分析创造条件。
机场;跑道道面;平整度;小波理论;细节信息
机场道面平整度是指道面面层相对设计基准平面的偏离。飞机驶过局部较为严重的凹陷区,凸台区,以及一定波长和波幅的波形表面隆起等不平整位置时,不仅会影响起落架寿命,还会增大飞行员的操作误差,影响乘客的舒适度及货物的完好。它会引起道面承受额外竖向荷载,致使该区域产生永久性的道面损坏,从而减少道面的服务年限。目前,全世界广泛采用国际平整度指标(IRI)作为机场道面平整度的评价指标,其通过数学分析得到道面纵向不平整的一个统计量。它只能反映一定长度相对道面不平整的平均状况,不能体现不平整是什么以及具体位置等细节信息。基于此,本文尝试通过小波分析道面纵断面(pavement roughness of longitudinal profile),得到评定机场道面平整度的另外一种描述尺度,即能最大细节地反映道面平整度的具体分布情况,一定程度上可以作为国际平整度指标评定机场道面平整度的一种补充,以便在机场道面管理系统中制定出更合理的维护和修筑方案。
1 可行性论证
国际平整度指标(IRI)的测定原理是采用四分之一车的数学模型,以规定标准速度V为80 km/h行驶在道路上,然后计算每公里距离内由系统产生的累积竖向位移量(m/km)。由于飞机和一般路面交通车辆有以下3方面不同:①飞机与道路行驶车辆结构设计不同;②飞机的滑行速度范围一般为0~360 km/h,而路面交通车辆的行驶速度范围一般为40~120 km/h;③飞机在跑道上滑行的动力学原理是要保证飞机能安全起飞和降落,而道面行驶车辆行驶的动力学原理是要保证车辆在道面稳定地高速行驶。因此,国际平整度指标作为机场道面的平整度评定指标不严谨。
Yi-heien Chen等人[1]模拟了从0.1~100 m的15种波长的机场道面纵断面,将其输入APRas软件,通过模拟不同机型和设置不同的滑行速度,得到飞机在滑行过程中的竖向动力响应和道面纵断面的波长息息相关。基于此,本文尝试从机场刚性跑道波长入手,对IRI作为其指标的一种补充分析。
信号分析技术可以用来研究道面的波长特性[2]。信号分析即是傅立叶变换分析,是将一个信号分解成一系列不同频率的连续正弦波的叠加。然而傅立叶变换在变换时丢去时间信息,在研究一种信号的傅立叶变换时,不能看到特殊情况发生的具体时间,傅立叶变换只是一种纯频率的分析方法。将道面纵断面视为一种信号,运用傅立叶变换后,我们将看不到纵断面粗糙部分尺度与具体位置等重要细节信息。所以,傅立叶变换不能用于道面纵断面波长的研究。
小波理论是处理信号的一种新的时频分析工具,其克服了傅立叶变换分析方法表示信息时能清楚地揭示出信号的频率特征但不能反映时间域上细节信息的缺陷,而该细节信息对道面平整度的反映对道路维护部门来说是非常重要的;当利用小波变换实施时频分析时,由于同时具有时间和频率的局部特性以及多分辨分析特性,使得对道面纵断面信号的处理变得相对容易[3]。
2 小波理论基础
小波(wavelet)是一种时频内具有紧支集或近似紧支集且具有正负交替“波动性”的小区域波。
2.1 基本小波和小波函数
设ψ(t)∈L2(R),L2(R)为平方可积的实数空间,其满足:
1)ψ(t)是连续的且现指数是衰减的;

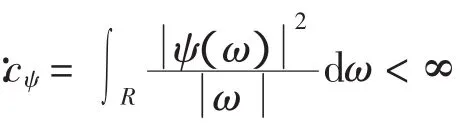
连续小波函数
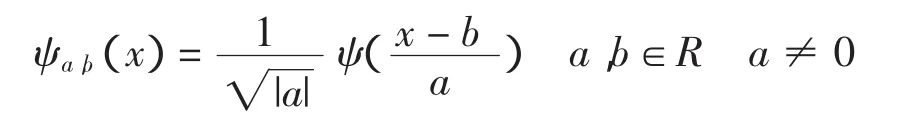
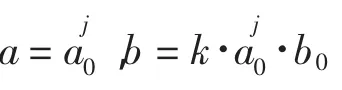
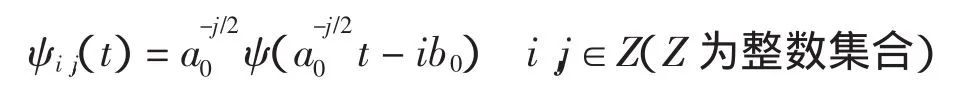
2.2 离散小波变换(DWT)
离散小波变换[5]来源于傅立叶变换,保证两者能量不变,将尺度因子与平移因子离散化,原始信号同时被离散化,表达式为离散小波变换
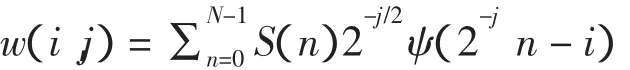
式中:i,j和 n 均为整数;w(i,j)是在尺度因子为j、平移因子为i时通过离散小波变换后得到的一组小波系数。将小波系数视为一个滤波器时,离散小波变换可通过滤波器组技术快速实现。Mallat算法可将原始纵断面信号f(t)首先分解一个低频部分a1和一个高频部分b1,然后重复对上一步低频部分分解成一个低频部分和一个高频部分,一直进行下去,表达式为
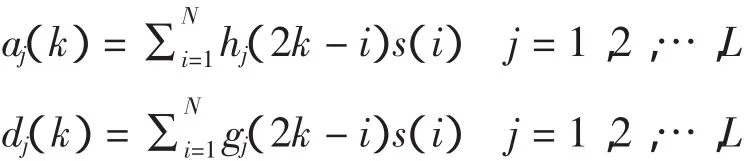
式中:L 为分解的层数,k=1,2,…n;aj是尺度因子为 j的低频部分;dj是尺度因子为j的高频部分;hj是尺度因子为j的低通滤波器;gj是尺度因子为j的高通滤波器,得到原始信号表达式
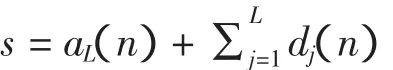
小波变换将道面纵断面信号f(t)分解成不同波长方法如图1所示,道面纵断面信号f(t)可以分解为一个高频部分(Detail)和一个低频部分(Approximation),低频部分又可以分解成高频部分和低频部分,低频部分再次进行分解,整个过程一直重复下去直到f(t)分解成一系列低频部分,得到一个小波分析树[1](Wavelet Decomposition Tree)。

图1 小波分析树Fig.1 Wavelet decomposition tree
3 选择分解道面纵断面的小波函数
采用小波变换分解前,必须找到分解f(t)的合适小波函数。现阶段广泛采用的方法是比较不同小波函数评定f(t)被分解后得到的所有纵断面(包括高频部分和低频部分)均方根误差(RMS error),选用其均方根误差最小的小波函数。文献[1]利用Daubechies小波系、Symlets小波系、Coiflets小波系的21种不同小波函数对输入的13种不同道面纵断面信号进行分析,得到Daubechies 3分解得到的均方根误差最小,所以本文采用Daubechies 3分解f(t)。本文编辑相应的Matlab程序得到Daubechies 3小波函数,如图2所示。

4 用小波变换分析机场道面纵断面
在信号处理中,小波分解主要优点在于其能反映信号中某处局部特征信息,即能体现信号f(t)的特征变化趋势、屈服点、高阶不连续点等细节信息。机场道面不可避免会有施工引起的局部拱起和长期磨损形成的沉陷、错台以及道面板块连接处断裂等局部不平整的细节信息。对于多数机场刚性道面,局部沉陷是一种很常见的疲劳损伤。当道面出现沉陷时,该区域高程波动很大,小波变换纵断面信号f(t)后,通过观察高频部分(例如d1)能检查出这些高程的波动幅度以及具体位置。
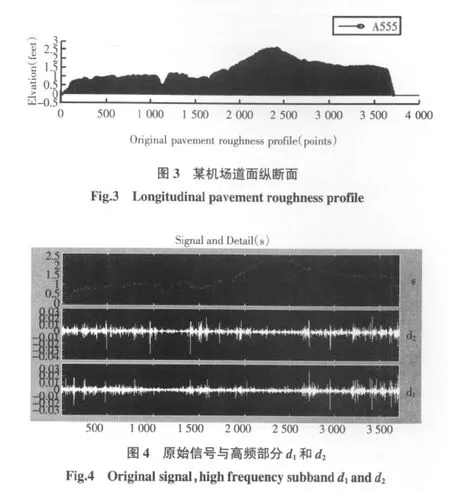
文献[6]表明分析机场道面面层纵断面时,对飞机滑行有影响的波长范围大于1.2 m,具体如表1所示。根据抽样定理,抽样间隔取2 feet能满足频率分解要求。已知某机场长度为2 260 m跑道,实测3 710点高程数据A555,每两点间隔为2 feet(0.6 m)。通过数据格式转化,将这组高程数据输入Matlab中得到roughness.mat,即道面纵断面信号f(t),如图3所示。然后用Matlab小波工具箱中Daubechies 3对roughness.mat进行一维离散小波(Wavelet1-D)分解,分解后得到层系数d1和d2如图4所示。
从表1可以看出,对机场道面平整度有影响的波长与飞机速度是密切相关。用小波变换道面纵断面信号时,小波系数d1和d2能反映1.2 m至4.8 m(4至16 feet)短波长范围内道面表面平整度的细节信息分布情况,像局部凹陷或隆起等小波长高程特征变化比较剧烈部位会在小波系数d1和d2中体现,从图4小波系数d1和d2中,在该波长范围内,约有24处凹陷和隆起以及其具体位置,其高程变化尺度约在9 mm(0.03 feet)内。当飞机一定速度滑行经过这些特征处时,飞机竖向重力加速度突然变化,道面该处荷载发生剧烈改变。由于飞机产生过大的震动,极大影响乘客舒适性,也加速该处道面破坏损伤。

表1 有影响的波长范围Tab.1 Ranges of wavelength
本论文采用各国学术界广泛使用的APRas 2.0仿真模拟软件对高程数据A555进行模拟分析,结果如图5所示。某飞机以速度v=22 km/h(12 knots),经过这些特殊点时,驾驶舱的竖向加速度(PSA)、飞机中心竖向加速度(CGA)、飞机前起落架处跑道道面承受的最大荷载(NGPL)、主起落架处道面承受的最大荷载(MGPL)突然改变。例如,从图4中获取一特征点A,坐标为(2716,0.029),其含义为在距跑道端feet(1 656 m)处,高程波动尺度为0.029 feet(8.84 mm)。A点对应于图5中5 430至5 446 feet的凹坑B,该凹坑高程最低点坐标为(5 432,24)。B凹陷区域内最大激励荷载和加速度如表2所示。
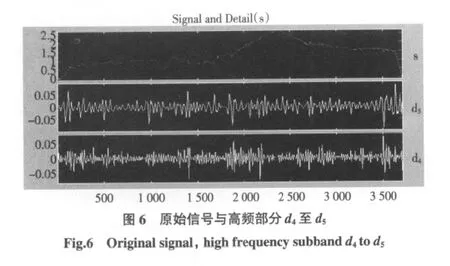
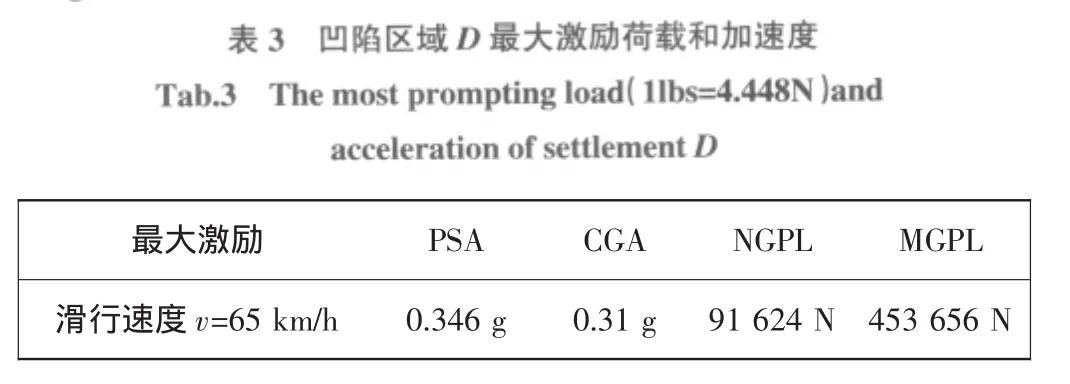
小波系数d3至d5能反映4.8~38.4 m长波的道面平整度细节信息,如图6所示。例如,d4能反映9.6 m~19.2 m的波长信息,取 d4中一特征点 C(3502,0.07),C 点对应图 7区域为 7 001~7 048 feet的凹陷区域D。从图7可以看到,某飞机以速度v=65 km/h(35knots)经过该区域时,D最大激励荷载和加速度如表3所示。
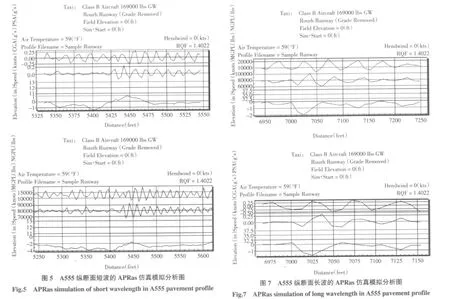

表2 凹坑B最大激励荷载(1 lbs=4.448 N)和加速度(g)Tab.2 The most prompting load(1 lbs=4.448 N)and acceleration of depression B
5 结语
?
1)小波变换可用于机场跑道纵断面高程数据分析,对机场道面平整度的具体分布情况作细节反映,克服单纯采用IRI描述机场道面纵断面的单一性和局限性。
2)可采用DWT将机场道面纵断面f(t)分解成不同频率的波长。
3)采用小波函数Daubechies 3对某机场道面纵断面高程数据A555进行一维离散小波分解,得到小波系数 d1、d2、d4和 d5。其中,小波系数 d1和 d2能反映1.2~4.8 m波长内道面表面不平整的细节信息,如局部凹陷或隆起等小波长高程剧烈变化的部位;小波系数d4至d5能反映9.6 m~38.4 m的长波道面表面平整度信息,如由地基沉降不均匀所致的不平整。
4)采用APRas2.0仿真模拟软件,对A555进行仿真模拟,得到凹坑B、凹陷区域D处的最大激励荷载和加速度值。
[1]YI-HSIEN CHEN,CHIA-PEI CHOU.Assessment of Aircraft′s Vertical Responses To Develop the Roughness Evaluation Index for Airport Pavement[C]//The 2004 Federal Aviation Administration Airport Technology Transfer Conference,Washington,DC:2004.
[2] 成智礼,王彤霞,罗 永.小波的理论与应用[M].北京:科学出版社,2004.
[3] 李建平,杨万年译.小波十讲[M].北京:国防工业出版社,2004.
[4]LIU WEI,T F FWA,ZHAO ZHE.Pavement Roughness Analysis Using Wavelet Theory[R].Center for Transportation Research,Dept of Civil Engineering National University of Singapore,2002.
[5] 周莉莉.用小波变换求解结构动力响应硕士论文[D].重庆:重庆大学,2006.
[6] 杨酒骏.按使用要求设计道面[M].北京:空军后勤部工程设计局,1980.
Detail Research of Airport Pavement Roughness Based on Wavelet Analysis
WANG Wei,HU Chun-fei
(The Airport College,CAUC,Tianjin 300300,China)
Wavelet theory analyzes airport rigid pavement roughness of longitudinal profile.A special pavement profile is disintegrated by the wavelet tool of MATLAB,the article obtains the fluctuation and location of long and short wave of the pavement roughness profile in different high frequencies, and fills up the lack of IRI.Meantime,it partly promotes aircraft-pavement dynamics analysis.
airport; runway pavement; roughness; wavelet theory; detail
V351.11
A
1674-5590(2011)01-0013-04
2010-10-20;
2010-11-29
王 维(1960—),男,河北丰南人,教授,硕士,研究方向为机场工程.
(责任编辑:李 侃)

