相应于一类幂零李代数的顶点代数结构
刘雪梅
(中国民航大学理学院,天津 300300)
相应于一类幂零李代数的顶点代数结构
刘雪梅
(中国民航大学理学院,天津 300300)
顶点代数和顶点算子代数在物理学领域有着广泛的应用,因此对其研究也有很大的实际意义。主要从有限维幂零李代数g出发,给出了g带有非退化对称不变双线性函数的条件,并构造了相应于g的一个代数结构,从同构的意义上证明了其满足顶点代数的条件,从而给出了一个新的顶点代数结构。
顶点代数;有限维幂零李代数;非退化对称;不变双线性函数
顶点代数和顶点算子代数的概念最早给出于1 9 8 6年和1 9 8 8年,由于其在物理学中的广泛应用,引起了数学界和物理学界的高度重视。R.E.B o r c h e r d s因在顶点代数及其相关领域的杰出贡献在1 9 9 8年世界数学家大会上获得菲尔斯奖,迄今为止已获得经典的顶点(算子)代数及其表示理论,以及概念的完备公理体系及其等价性质,但现有的应用已知的代数系统构造出的顶点代数的实例并不多[1-3],本文先证明了一类有限维幂零李代数带有非退化对称不变双线性函数的条件,在此基础上给出了相应于此类有限维幂零李代数的一个顶点代数结构。
1 顶点代数的基本概念
从文献[3]和文献[4]中引入以下符号和定义。
令 Z+、Z-、Z、N、C 分别表示正整数、负整数、整数、非负整数和复数集。
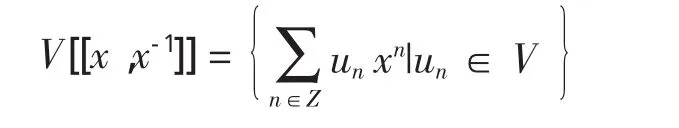
设V是C上的向量空间,定义称V[[x,x-1]]为形式罗朗级数向量空间。

称V[[x]]为非负形式罗朗级数的向量空间。
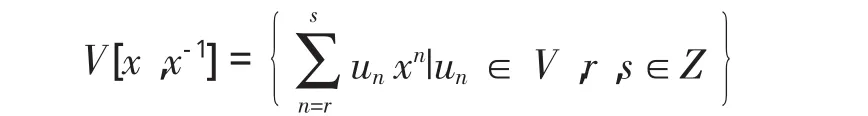
称V[x,x-1]为罗朗多项式环。
定义1 设V是复数域C上的向量空间,如果存在一个线性映射
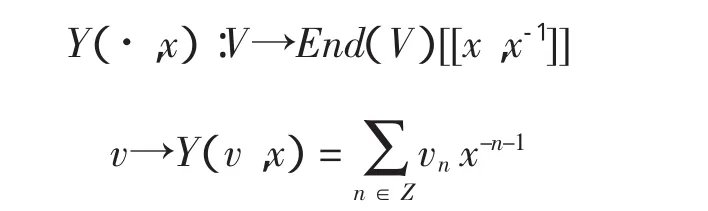
其中vn∈End(V),n∈Z,并且满足下列条件:
1)对于任意的u,v∈V,当n充分大时有unv=0。即 Y(u,x)v ∈ V((x))(截头条件)。
2)V 中存在一个向量,记为 1,满足:Y(1,x)=1V,称1为真空向量(真空性质)。
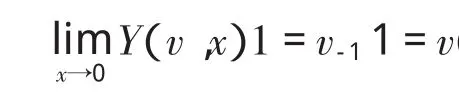
4)对任意的 u,v∈ V,有
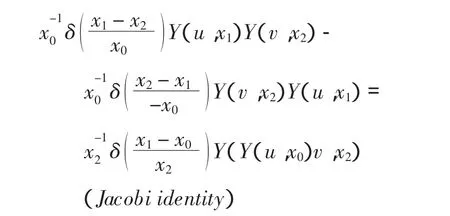
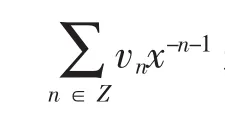
引理1 令V是一个向量空间,1∈V,设T是V的子集,并存在一个线性映射

其中a是T中任意元,那么Y0能被唯一扩充成从V到 Hom(V,V((x)))的线性映射 Y,满足(V,Y,1)具有一个顶点代数结构,顶点算子映射Y由以下形式给出
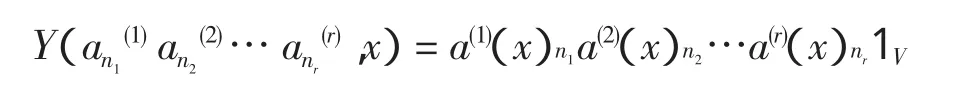
2 带有双线性函数的幂零李代数
从文献[5]和文献[6]中,引入以下结论。
引理2 设g是复数域上的有限维幂零李代数,g的元素集合S={x1,x2,…,xl}称为g的一个极小生成元系当且仅当
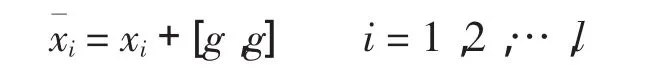
若 g是幂零李代数,记 g1=g,gk=[g,gk-1],k=2,3,…。使得gN+1=0,gN≠0的正整数N称为g的幂零指数。由 gN+1=[g,gN]=0,知 gN⊆C(g),C(g)是 g 的中心。
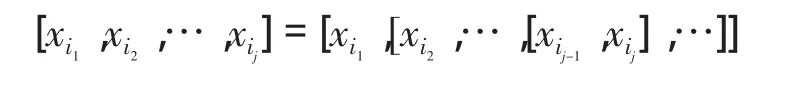
任取 g 的极小生成元系 S={x1,x2,…,xl},记称其为j次单项。用J a c o b i等式不难证明g中的每一个元素都可以表示成有限个单项的线性组合。令
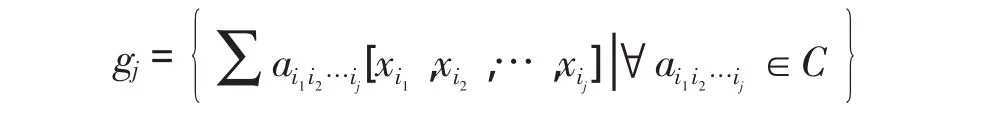
称 gj,j=1,2,…,N 是 g 的 j次齐次子空间。且有

是子空间的和,显然有
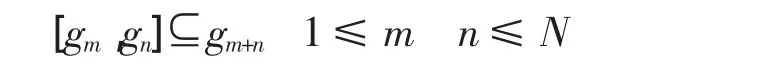
其中gk=0,当k>N 时,gN=gN。
定义2幂零指数是N的有限维幂零李代数g称为可阶化的,如果(*)式为子空间的直和。
定义3 幂零李代数g称为不可分解的,如果g不是非零理想的直和。
设g是一个有限维复李代数,(x,y)是定义在g上的对称双线性函数,如果对∀x,y,z∈g,有
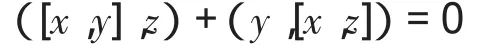
则称此双线性函数满足不变性。
定理1 设g是不可分解,可阶化有限维复幂零李代数,型为 l,幂零指数为 N,C(g)是 g 的中心,S={x1,x2,…,xl}是 g 的一个极小生成元系,g 关于 S 的齐次子空间的直和分解为g=g1+g2+…+gN,若满足:
1)C(g)=gN,且 d i mgN=l;
2)存在 gN的基{y1,y2,…,yl},对 gN中任意由 N 次单项构成的基{μ1,μ2,…,μl},由{y1,y2,…,yl}到{μ1,μ2,…,μl}的过渡矩阵Au=(aij)具有以下性质,即对表达式μj=[xj11,xj2,…,xjN]=a1jy1+… +aijyi+… +aljyl中,如果[xi,xj1]=0,对 xi∈S,则 aij=0。那么 g 带有非退化不变对称双线性函数。
证明:已知 S={x1,x2,…,xl}是 g1的基,取定 gN的由 N 次单项构成的基{μ1,μ2,…,μl},已知 μj=a1jy1+… +aijyi+… +aljyl,j=1,2,…l。对∀xi∈S,定义 g1+gN上的对称双线性函数(x,y)如下:
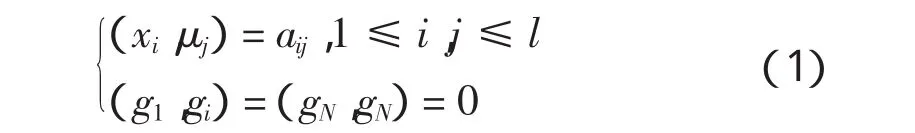
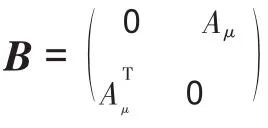
当i+j≠N+1时,规定(gi,gj)=0,对i用数学归纳法可在上gi+gN+1-i递归的定义(x,y)且易证这样定义的(x,y)是g上的非退化对称双线性函数。
3 相应于g的顶点代数结构
定义4 设g是上述带有非退化对称不变双线性函数(,)的幂零李代数,令
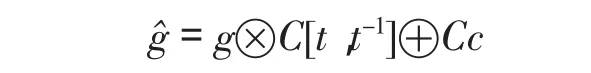
其中C[t,t-1]是 t的罗朗多项式环,c是的中心,如下定义的李积运算
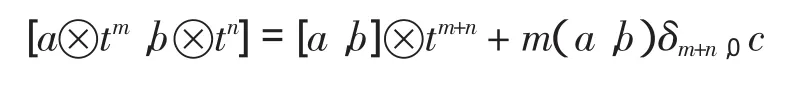
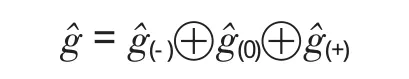
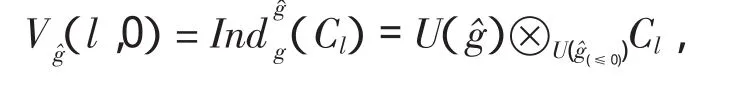
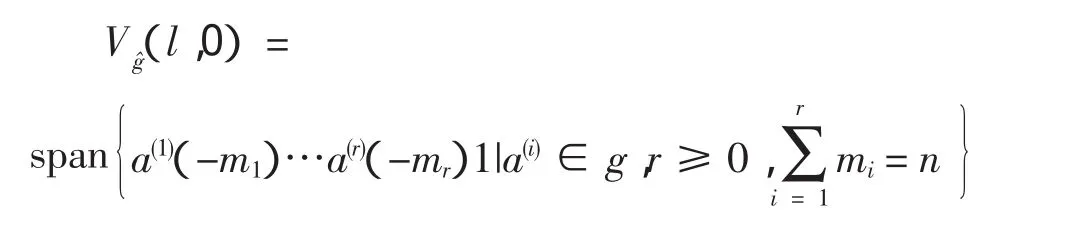
由PBW定理知:
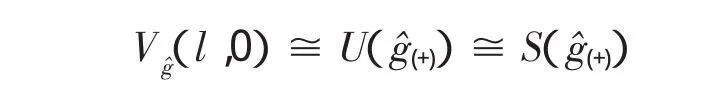
定理2V(l,0)是一个顶点代数。
证明:定义映射π∶g→V(l,0),π(a)=a(-1)1,则在映射π下,g作为V(l,0)的子集,由引理1,令V=V(l,0),T=g,Y0(a,x)=Y0(a(-1)1,x)=a(x),a∈g,则V(l,0)是一个顶点代数。
[1]刘雪梅.相应于一类对称自对偶李代数的顶点代数结构[J].数学的实践与认识,2 0 0 9,3 9:1 7 5-1 7 8.
[2]刘雪梅,李 立.素特征域上的顶点代数结构[J].中国民航大学学报,2 0 0 7,2 5:6 2-6 4.
[3]LEPOUSKY J,H-S LI. Introduction to Vertex Operator Algebra andTheir Representation[M].Boston:Progress in Math,2003.
[4]ADAMOVI D. Vertex operator algebras and irreducibility of certainmodules for affine Lie algebras [J] . Math Res Lett,1997,4:809-821.
[5]JACOBSON N. Lie Algebras Interscience Publishers[M]. Shanghai:Shanghai Sci and Tch Publishers,1964.
[6]王书琴.一类带有非退化不变对称双线性函数的幂零李代数[J].数学学报,2 0 0 0,4 3:5 6 1-5 6 8.
Vertex Algebra Associated with a Class of Nilpotent Lie Algebras
LIU Xue-mei
(Science College, CAUC, Tianjin 300300, China)
Let g be a nilpotent Lie algebra, in this paper, proves conditions for of a class nilpotent Lie algebra with symmetric, invariant, non-degenerate bilinear from and a vertex algebra associated to g is presented.
Vertex algebra; Nilpotent Lie algebra; non-degenerate symmetric; invariant bilinear from
O152.5
A
1674-5590(2010)02-0059-03
2009-00-00;
2010-00-00 基金项目:中国民航大学科研基金(2010kys04)
刘雪梅(1977—),女,黑龙江省呼兰人,讲师,理学硕士,研究方向为李代数与顶点代数.
(责任编辑:李 侃)

