动态板形辊平整机板形控制机理模型研究
刘志亮 李文强 王英杰
1.燕山大学,秦皇岛,066004 2.宝钢股份公司,上海,200900
0 引言
平整是轧制工艺过程中的最后阶段,平整轧制是生产优质薄板、确保带钢成品质量的最后一道工序。对冷轧后退火的带钢或热轧后的带钢进行平整,对提高产品质量、控制板形以及表面状态起着重要的作用。平整的实质是一种小压下率(0.5%~4.0%)的二次冷轧变形,主要作用有:改善带钢板形;改善带钢力学性能,消除退火带钢的屈服平台;改善带钢表面质量,使其达到一定的表面粗糙度要求。
动态板形辊(dynamic shape roller,DSR)技术是法国克莱西姆(Clecim)公司于20世纪90年代研制成功的一种轧制力分布控制技术,作为第三代板形技术的典型代表,体现了板形控制技术的最新发展。目前,我国的平整技术设备与工艺基本实现了国产化,但是缺乏关键的核心技术,平整技术设计和控制模型相对落后,从国外引进的设备,由于技术封锁,缺乏配套的先进模型,故平整质量不高。因此,从基础理论及对实际的平整机技术进行研究,对掌握平整机核心技术具有重要的意义[1-2]。
1 相关数学模型
根据DSR技术的特殊板形控制原理,基于影响函数法建立DSR平整机板形控制特性分析模型。目前对DSR技术的研究都是利用有限元软件建立三维模型来对其板形控制能力进行界定的,模型简化较多,计算量大,仅可以做定性的分析,可移植性差,不能够应用于在线控制。本文综合考虑了芯轴与辊套的特殊结构以及分段液压压块机构的影响,采用分割模型建立DSR平整机的辊系变形模型,在此基础上,考虑平整轧制过程的特点,将针对平整过程的金属模型和辊系模型进行耦合计算,建立分析DSR平整机板形控制特性的整体模型,并给出了计算流程。
板形控制模型主要有基于轧机基本理论的机理模型和基于经验与数据的智能模型。智能模型主要从数据中总结和归纳因果关系,模型简练,计算速度快,但模型的建立依赖于实际数据与实际经验,分析与预测能力较弱,通用性较差。机理模型的结构相对复杂,通过严谨的理论推导加上一定的合理假设,具有很强的分析预测能力,对实际的生产应用和新的板形控制技术的开发都有重要的指导意义[3-5]。
完整的板形控制机理模型共包括8个子模型[6],即金属变形模型、辊系弹性变形模型、轧件和轧辊的温度场模型、辊系磨损模型、板形良好判别模型、板形偏差模式识别模型、板形标准曲线模型和板形控制策略模型。
2 DSR平整机板形控制机理模型的建立
2.1 DSR平整机辊系受力模型
本文采用影响函数法计算辊系弹性变形,图1以支承辊辊身长度L为离散长度,考虑到动态板形辊各段压块力的受力情况,压块力一般为5段或7段,为了使计算更具一般性,假设沿辊身长度共作用有k个压块,每个压块的压块力从左到右分别记为T1,T2,…,Tk,每个压块段的长度分为m个等分单元,总的单元数N=km,每个单元宽Δx=L/N,作用于轧辊上的载荷亦按相同单元离散化。以左压下支点处为原点,各单元中心的横坐标为xi(i=1,2,…,N),将轧制压力分为n份,轧制压力和辊间压力在第j段内分别用集中力 p j、qj代替。
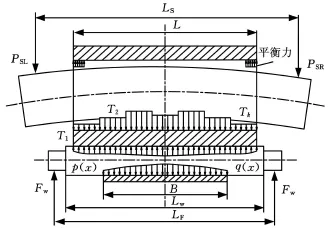
图1 DSR平整机辊系力学模型
2.2 DSR平整机辊系变形模型的建立
2.2.1 非对称轴线挠曲影响函数的计算
由于本课题涉及分段压块力左右不对称分布力的作用,故计算轴线挠曲位移需要此种情况下的影响函数。影响函数的计算将轧辊看作两端自由支承的简支梁,将辊身沿轴向划分为N个单元,轧辊轴线挠曲的影响函数α(i,j)即是当轧辊在j单元受到单位力时在i单元产生的轴线位移。图2为非对称影响函数的计算示意图。
当xi≤xj时,
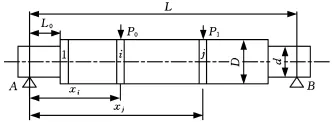
图2 非对称影响函数计算示意图

式中,k为剪切系数,圆截面时k=10/9,空心圆截面时k=2;G为轧辊剪切模量,GPa;E为轧辊弹性模量,GPa;Id、ID分别为直径d、D的圆截面轧辊惯性矩,mm4;Ad、AD分别为直径d、D的圆截面面积,mm2。
2.2.2 支承辊轴线位移
考虑到动态板形辊具有芯轴和辊套的结构,其芯轴的挠曲只发生在轧辊内部,只有在边部影响到辊套与芯轴的相对位置,因此本文将首先计算芯轴的挠曲变形和刚性位移,由于芯轴的位移发生在DSR辊内部,故对带材的厚度控制起作用,但是不改变辊缝的形状分布,芯轴对辊套起支撑的作用。在此基础上计算辊套整体的挠曲位移以及刚性位移。
当xi≤xj时,

式中,EXb为芯轴弹性模量;IXb为芯轴惯性矩;GXb为芯轴剪切弹性模量;AXb为芯轴横截面面积。

则所有压块力共同作用时产生的位移为
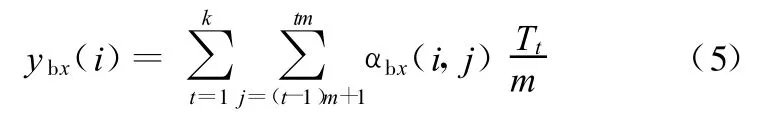
辊套位移分为其相对于辊身端部的挠曲位移和刚行位移。挠曲位移的计算可以假设辊身端部有简支约束,然后分别计算在分段压块力和辊间压力作用下的辊套位移:

式中,αbt(i,j)为辊套挠曲影响函数。
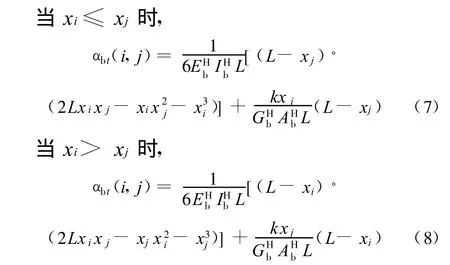
式中,EHb为辊套弹性模量;IHb为辊套惯性矩;GHb为辊套剪切弹性模量;AHb为辊套横截面面积。
式(6)~式(8)中,剪切系数k取2。支承辊辊套刚性位移:

式中,b1、b2分别为辊套左右两端的轴线位移。
2.2.3 工作辊轴线位移
工作辊轴线的位移由四部分组成,即刚性位移、轧制压力引起的挠曲位移、辊间接触压力引起的挠曲位移和工作辊弯辊力引起的挠曲位移。
工作辊挠曲位移为
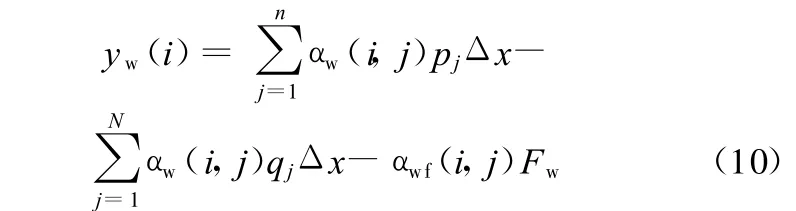
式中,αw(i,j)为工作辊挠曲影响函数;αwf(i)为工作辊弯辊影响函数。
当xi≤xj时,
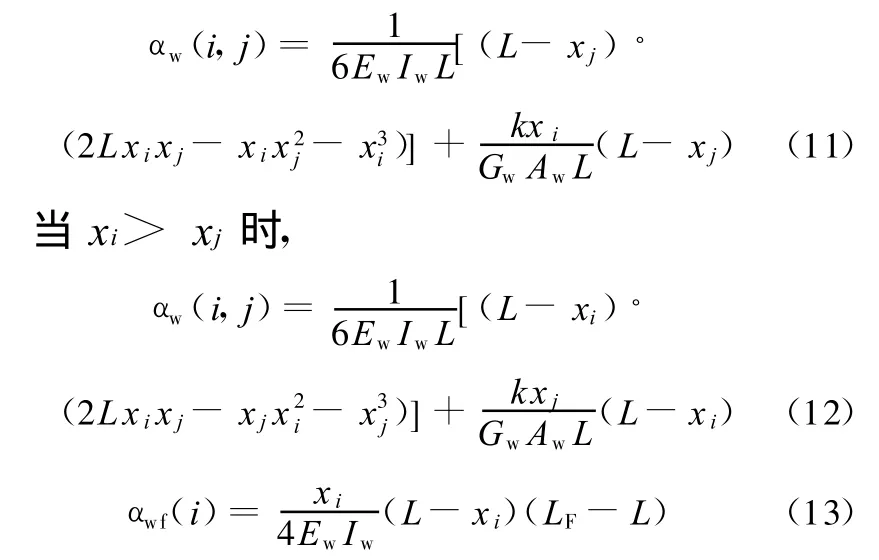
式中,Ew为工作辊弹性模量;Iw为工作辊辊身惯性矩;Gw为工作辊剪切弹性模量;Aw为工作辊辊身横截面面积。
工作辊刚性位移为
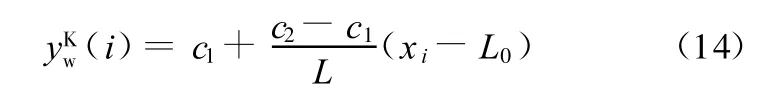
式中,c1、c2分别为工作辊左右两端的轴线位移。
2.2.4 轧辊压扁的计算
工作辊与支承辊之间的弹性压扁量,即两轧辊中心线的接近量δwb(i),按照平面应变条件下的半平面体模型求解:
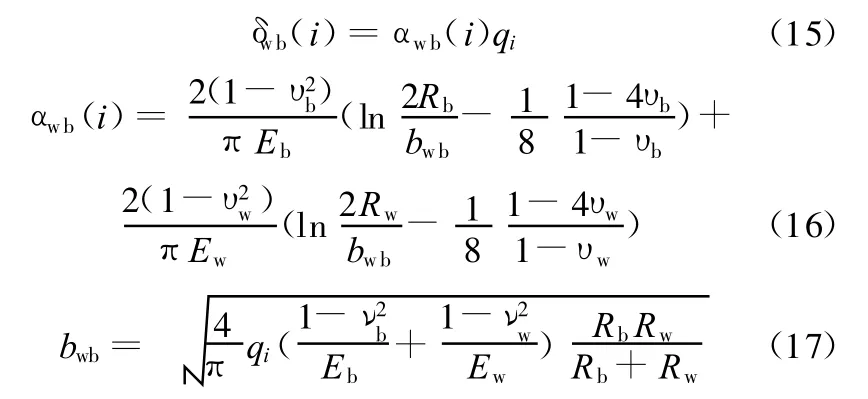
式中,αwb(i)为辊间的弹性压扁量影响系数;Rw、Rb和υw、υb分别为工作辊与支承辊辊身半径和泊松比;bwb为辊间接触压扁半宽度。
由于支承辊辊套的空心结构以及特殊的受力情况,使得辊套不仅承受辊间压力,同时还受到一个附加的弯矩载荷作用,这使得辊套在接触点的曲率半径增大,在上述计算压扁的时候需要用新的曲率半径Rt代替辊套原来的辊身半径R0,得到更准确的辊间压扁量[7]:
式中,R1、R0分别为辊套的内外半径。
工作辊与轧件接触表面的压扁可按半空间模型来求解:
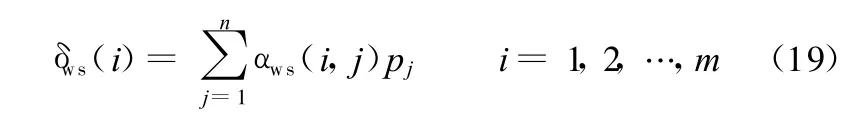
式中,αws(i,j)为工作辊与轧件的接触压扁影响系数。
工作辊和支承辊辊套位移的协调方程为
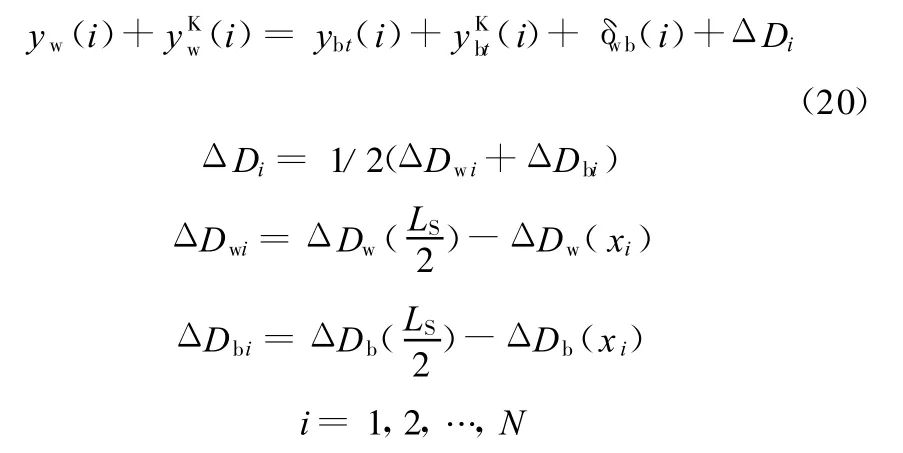
式中,ΔDi为辊间原始间隙或空载凸度。
DSR辊的特殊芯轴与辊套结构使其在板形控制的同时不影响厚度控制,芯轴在压块力的作用下产生挠曲变形,但此变形在DSR内部,可以通过压块位移的调节来补偿,从而不会影响辊缝几何形状的控制。DSR的辊套位置由芯轴两端的定位轴承来保持其轴向位置,边部两压块调节其与芯轴的相对位置,可满足辊缝和控制的要求。辊身中点处的辊缝值可以表示为由辊系变形部分所引起的辊缝值变化量和其他支撑结构变形引起的辊缝值变化量。
由上述计算可以求得辊间压力分布,轧件出口厚度的横向分布为
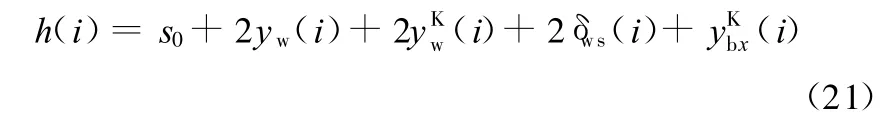
2.3 DSR平整机板形控制机理模型的建立
板形控制分析需要金属模型和辊系变形模型耦合迭代计算。金属模型确定轧件的单位轧制压力和前后张力横向分布等内容,但需要辊系变形模型提供轧件出口厚度的分布,而辊系变形模型计算中需要轧制力的分布作为前提条件,在相互迭代的计算中得到符合要求的结果。板形控制特性分析的流程图如图3所示。

图3 分析的流程图
2.4 DSR平整机承载辊缝的调控功效
将模型应用在2030mm平整机的上支承辊,得到板宽为1800mm时各调节机构的辊缝调控功效曲线,如图4~图11所示。其中弯辊力的调节量为100k N,7个压块力(T1~T7)的调节量为500k N,各调控功效都是在其他调节机构处于基态时得到的。
可以看出,各压块力的作用关于中间压块是对称的,这是由其结构决定的,分析中将只计算前四个压块力T1~T4(以500k N为一个调节单位)和工作辊弯辊(以100kN为一个调节单位)。其中各调控功效曲线的形式较复杂,呈高次曲线的形态,文献[6]对有限元软件模拟的结果用五次多项式可以对调控功效曲线进行较好的拟合,本文的计算结果与文献[6]中的研究结果相符。T1和T7压块力调节量对辊缝的调节范围较小,而且只有在边部才有一定效果。T2和T6可以实现宽度方向上20μm以上的变化量,曲线形式处于过渡形式。从T1和T7到 T3和 T5的时候,曲线的弯曲方向变为相反的方向。中间压块力T 4的调控曲线幅值较弯辊相对小一些,但是其变化趋势比弯辊急速。对于普通轧机的弯辊,对辊缝的调节能力在边部较明显,在中部效果减弱,从本文的结果也可体现这一点,压块力 T4直接作用于辊套的中部,对中部的影响较大一些。本文的结果与文献[8]在2030mm冷连轧机的ANSYS有限元仿真结果相比,曲线的形式基本相同。
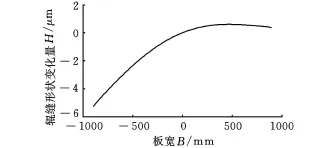
图4 压块力T 1的板形调控功效曲线
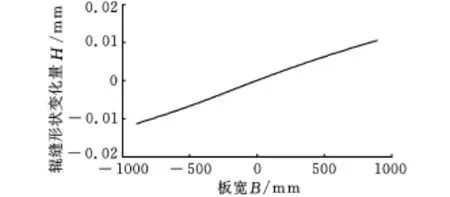
图5 压块力T 2的板形调控功效曲线

图6 压块力T 3的板形调控功效曲线
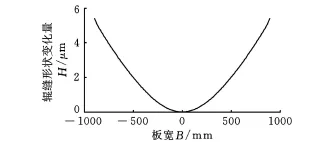
图7 压块力T 4的板形调控功效曲线

图8 压块力T 5的板形调控功效曲线

图9 压块力T 6的板形调控功效曲线
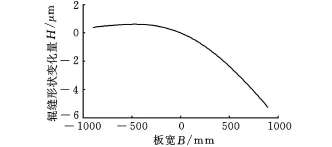
图10 压块力T7的板形调控功效曲线
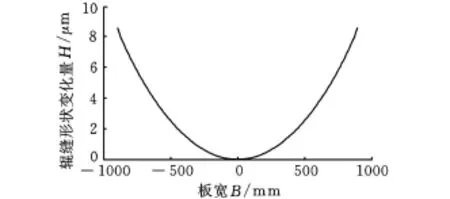
图11 弯辊力F w的板形调控功效曲线
3 结束语
针对平整机的特殊性,基于分割模型的影响函数法,充分考虑DSR技术的特殊控制原理,建立了DSR平整机辊系变形模型。将针对平整过程的金属模型和辊系模型进行耦合计算,建立了板形分析的整体模型,并编写了模型的计算流程和程序,以此对DSR平整机的板形控制能力进行研究。本文的研究结果具有很好的应用价值。
[1] 连家创.刘宏民.板厚板形控制[M].北京:兵器工业出版社,1995.
[2] 戚向东,连家创.考虑轧件弹性变形时冷轧薄板轧制压力分布的精确求解[J].重型机械,2001,23(5):41-44.
[3] 白振华.冷带钢轧机板形控制技术的开发研究[D].秦皇岛:燕山大学,2002.
[4] 曹鸿德.塑性变形力学基础与轧制原理[M].北京:机械工业出版社,1981.
[5] 华建新,金以慧,吴文彬.基于动态板形辊的冷轧板形控制新技术[J].钢铁,2001,36(1):33-37.
[6] 周西康.DSR冷轧宽带钢轧机板形控制性能研究[D].北京:北京科技大学,2005.
[7] 吴文彬.板形控制新技术在宝钢2030冷轧轧机的应用与研究[D].沈阳:东北大学,2003.
[8] 张清东,王文广,周晓敏,等.DSR宽带钢冷轧机的特殊板形控制性能[J].北京科技大学学报,2008,30(2):71-76.

