一种非对称共面波导相位补偿弯曲结构

李晓明 房少军 付世强

(大连海事大学信息科学技术学院，辽宁 大连 116026)

1. 引 言

近年来，共面波导(CPW)以其易于串并联、低损耗、低色散、集成度高等优点得到了越来越广泛的研究，并广泛应用于微波集成电路之中，有关CPW不连续性的研究也已较为深入[1-2]。弯曲结构在微波集成电路中是一种常见的不连续性结构，其对电路特性的影响是不容忽视的。CPW弯角处的不对称性，使电波在两条缝隙的传播中存在路程差，从而导致两侧信号的相位不一致并激发奇模，而这种传输模式在一般信号传输中是不需要的甚至有害的，应加以抑制。

为抑制弯曲结构所激发的奇模，通常采用空气桥[3-4]及拐角斜切[5]等方式加以补偿。文献[6]提出了一种速度补偿型弯曲CPW结构，该结构采用在CPW较长缝隙中的介质上周期打孔的方式，降低其等效介电常数，以改变信号在该槽中的传输速度，从而使两侧信号的相位在输出端达到一致。这种方式为抑制弯曲结构中的奇模提供了新思路，但也有其局限性：首先，从工艺上讲在介质上打孔的复杂度和难度明显高于普通PCB刻蚀；其次，在介质上打孔事实上已改变传输线的有效介电常数，除改变传输线一侧的相速外，也影响到整个传输线的特性阻抗，对于原先设计为直通的CPW弯曲结构，中间引入一段特性阻抗不同的传输线，必然会使整体的匹配恶化。

本文提出了一种非对称共面波导(ACPW)相位补偿结构。该结构通过在弯曲共面波导一侧的金属地和中心导带上引入一种形似波纹的形状，该结构由CPW、ACPW及渐变ACPW短截线相连而成，这种结构有效增加了弯角中波程较短一侧缝隙的波程，从而使中心导带两侧的信号传输实现相位均衡。由于该结构采用了ACPW短截线及ACPW渐变线，整个结构的特性阻抗得以保持在50 Ω附近，具有较好的插入损耗和回波损耗。与文献[6]所提出的补偿结构相比，本文的结构只需对介质板一侧的金属层进行刻蚀加工，工艺简单，设计方便，能有效地降低制作成本。

2. 结构说明

传统弯曲CPW结构如图1所示。电磁波在槽1和槽2中传播，经由槽2传播的电磁波比经槽1传播的电磁波要走行更远的路程，两束电磁波的波程差为Δl=l2-l1.正是这种波程差使弯曲结构中的两束电磁波存在相位差，并因此激励起奇模。

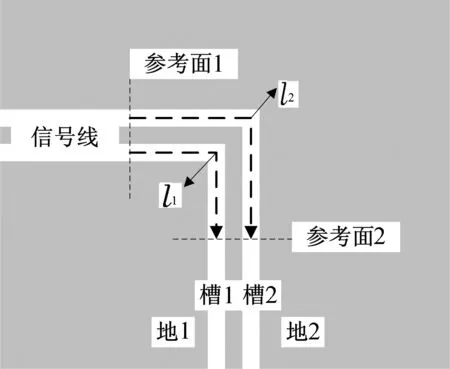
图1 CPW弯曲结构示意图

(a)所提出ACPW弯曲结构

(b)参数说明图2 所提出ACPW弯曲结构及参数说明

在本文的计算和仿真中，图2所示的部分参数选取如下：CPW中心导带宽度Wc=0.3 mm，缝隙宽度Ws=0.2 mm，介质板厚度h=0.65 mm，金属层厚度t=0.018 mm，介质板介电常数εr=9.6，在此尺寸下，CPW的特性阻抗Z0≈50 Ω.

3. 理论分析

具有金属底板的ACPW结构如图3所示，当两槽的宽度Ws1=Ws2=Ws时，为对称CPW；否则为ACPW。ACPW的单位分布电容可分为三个部分：中心导体与两侧地的电容C1、C2，以及中心导体与底板间的电容C3，总的单位分布电容C0=C1+C2+C3.当传输线为对称CPW时，C1=C2，C0=C1×2+C3.

图3 具有金属底板的ACPW示意图

就微带线而言，在给定介质介电常数、厚度的前提下，为实现某一特性阻抗，只能使用唯一的尺寸；与之相比，CPW可以在选定介质参数后，通过选取不同的Ws和Wg获得同一特性阻抗的一系列尺寸，因而其设计较微带线更为灵活。ACPW比CPW多一个设计参数，因此，在设计上具有更高的灵活性，而CPW也可看作ACPW的一个特例。

微波传输线的特性阻抗可由式(1)计算，其中εeff为传输线的等效介电常数，其定义由式(2)给出。式(2)中，C(εr)为传输线的单位分布电容，C(εr=1)为将传输线中的填充介质由空气替换的分布电容。将式(2)代入式(1)后，可得到特性阻抗与电容间的关系(3)。由文献[7]中单位分布电容的求解公式可知，对CPW传输线而言，增加中心导带Wg的宽度或减小槽宽Ws都可以增加单位分布电容，这对于介质填充和空气填充两种情况都是成立的，那么由式(3)就可以得出：随着Wg的增大或Ws的减小，传输线的特性阻抗Z0也是减小的。

(1)

(2)

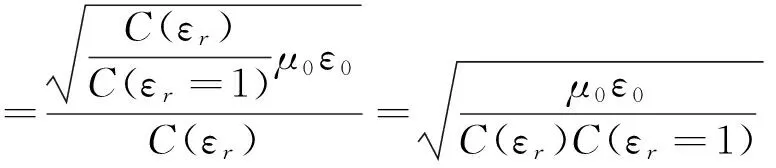
(3)

相比于CPW，ACPW拥有一个额外的设计参量，因此，为实现同样阻抗的传输线，ACPW有更加灵活的设计方式。由文献[8][9]的计算公式可知，在其他参数不变的情况下，单独减小槽宽Ws1或Ws2，仍可增加传输线的单位分布电容。由此可知，保持Ws1不变，而在增大Wg的同时适当增大Ws2，仍可使传输线的特性阻抗保持在50 Ω。

采用保角变换法[8]可计算ACPW的特性阻抗。在本文中令Ws1=Ws，以Ws2为变量，Wc为参变量进行了计算，并将计算结果绘于图4。从图4的曲线可以看出，随着Ws2的增大，ACPW的Z0也将增大，这与上述的分析相符；但需要注意的是，随Ws2的增大，Z0增大的速度是逐渐减慢的。随着Wc的增加，Z0逐渐减小，并且Z0随Wc变化的幅度要比随Ws2变化的显著。当Wc≥0.4 mm时，即使Ws2增大到0.5 mm，Z0仍不能达到50 Ω，这是因为改变Ws2只能改变图4中的C2，当Ws2低于某一阈值时，C2的值将趋于0，此时Ws2的改变将不再对Z0产生影响。本文选定Wc′=Wc+ΔWc=0.35 mm，由图4可找到对应于Z0=50 Ω的Ws2，即Ws2=0.3 mm，此时ΔWg=0.15 mm。将此参数的ACPW用于图2所示结构中，即可实现特性阻抗一致的波纹状结构。

图4 ACPW特性阻抗Z0与参数Wc及Ws2的关系

4. 仿真计算

为证明所提出结构在补偿弯曲结构两槽间相位差的有效性，本文采用 CST Microwave Studio 5进行了大量的时域仿真。仿真中在弯曲结构的两侧分别以高斯脉冲为激励，在弯曲结构另一侧的两槽中分别加入探针，以观测各自接收到的时域信号。图5为对传统弯曲CPW进行仿真的波形，容易看出，槽1和槽2检测到的信号除幅度有小量差别外，波峰的位置也有所不同，这体现了电磁波沿两槽传播时所形成的波程差，本文记两路信号的时延差为Δt，则当Δt=0时，两路信号的相位在输出端达到一致。本文所引入的结构，目的即是消除这种时延差，以减弱奇模对正常传输模式的影响。

图5 CPW弯曲结构中心导体两侧时域信号的比较

为探求所提出ACPW弯曲结构各参数对时延差的影响，采用以下参数进行了仿真：Wc=0.3 mm，ΔWc=0.1 mm，Ws=0.2 mm，ΔWg=0.15 mm，h=0.65 mm，t=0.018 mm，εr=9.6，以及不同的ACPW单元数n和不同的l0。其中，l0分别取0.1 mm，0.05 mm，0.03 mm；而相应的n则分别取1-8，3-16，4-10、15、20、25。针对各组数据仿真所得的时延差列于表1。

表1 所提出ACPW弯曲结构的时延特性

与单纯n或l0对时延差Δt的影响相比，我们更关心在单位长度上，所提出结构对两槽相位差的改善能力。我们采用ACPW波纹结构的总长度L=n×4×l0作为横坐标，以弯曲结构两侧的时延差Δt作为纵坐标，将表1中的三组数据绘成曲线，以直观展现不同l0在单位长度上改善信号时延差的效果，所绘曲线见图6。可以看出，随着ACPW单元数n的增加，时延差Δt呈下降趋势，并且与n存在线性关系；随着l0的减小，Δt下降的斜率变大。为了使Δt达到0，可以通过作图找到曲线与横轴Δt=0的交点，确定对应的n值，从而确定能提供有效相位补偿的ACPW弯曲结构的参数。事实上随着n的增加，数值计算所占用的内存和CPU时间也大大增加。在本文所进行的仿真中，在计算l0=0.03 mm，n=25的情况时，已达到所用计算机的计算极限，如欲进一步提高n以减小Δt的数值将无法进行数值计算，此时利用Δt与n间明显的线性关系，可以在有限的计算条件下对所提出的ACPW参数做出准确的设计。

图6 ACPW弯曲结构时延特性与结构长度关系曲线

5.实验结果与分析

弯曲结构中所激发的奇模是正常传输中不需要的，对共面波导传输线而言，转化为奇模的部分能量是损耗的一部分，因此，弯曲结构中对奇模的抑制同样影响着频率特性。我们对传统CPW弯曲结构和所提出的ACPW弯曲结构进行了频域仿真，为便于加工，重新选取参数如下：Wc=0.6 mm，ΔWc=0.2 mm，Ws=0.4 mm，ΔWg=0.3 mm，h=0.8 mm，t=0.018 mm，εr=9.6。仿真结果如图7(a)所示。从频域仿真结果可以看出，所提出结构的插入损耗较传统CPW结构有明显改善。我们对ACPW弯曲结构进行了加工，加工结构如图7(b)、7(c)所示，并将实测结果与仿真结果进行了对比，如图7(d)所示。由于实际加工中接头的焊接不理想，以及加工精度的限制，整个结构的插入损耗与仿真结果相比较大，但实测结果仍与仿真结果具有较好的一致性，从而说明所提结构的有效性。

(a) ACPW弯曲结构及CPW弯曲结构频域仿真对比

(b) ACPW弯曲结构实物图

(c) ACPW结构局部

(d) ACPW测试与仿真结果对比图7 频域仿真及测试结果

6. 结 论

本文提出了一种采用非对称共面波导进行相位补偿的弯曲共面波导结构，该结构可有效改善传统共面波导中心导带两侧的相位差，抑制所产生的奇模，同时具有等阻抗特性。此外，本文还针对该结构提出了一种结合数值计算的可行设计方法。对提出的结构进行了理论分析、数值仿真和加工测试，分析、计算和测试的结果证明了这种结构的有效性。

[1] 高 初,王蕴仪. 应用模拟退火算法建立共面波导结构的等效电路[J]. 电波科学学报, 2005, 20(4): 487-490.

GAO Chu,WANG Yunyi.Equivalent circuits of coplanar waveguide structures using simulated annealing method[J]. Chinese Journal of Radio Science, 2005, 20(4): 487-490. (in Chinese)

[2] 陈 鹏,李晓明,房少军,等.一种超宽带非对称共面波导-槽线转接器的研究[J].电波科学学报, 2010, 25(3): 559-562.

CHEN Peng,LI Xiaoming,FANG Shaojun, et al.Novel UWB ACPW-slotline transition[J]. Chinese Journal of Radio Science, 2010, 25(3): 559-562. (in Chinese)

[3] DIB N I, KATEHI, P B, PONCHAK G E. Analysis of shielded CPW discontinuities with air-bridge[C] //IEEE MTT-S Int. Microwave Symp. Dig., Boston, July 1991:469-472.

[4] OMAR A A, CHOW Y L. A solution of coplanar waveguide with air-bridges using complex images[J]. IEEE Tran. on Microwave Theory and Techniques, 1992, 40(11): 2070-2077.

[5] WATSON P M, GUPTA K C. EM-ANN modelling and optimal chamfering of 90° CPW bends withair-bridges[C] //IEEE MTT-s Int. Microwave symp. Dig., Denver, CO, June 1997:1603-1606.

[6] 张 卉，王均宏.奇模抑制孔缝阵列速度补偿型弯曲共面波导[J]. 电波科学学报，2009，24(2): 228-232.

ZHANG Hui, WANG Junhong. Velocity compensated CPW bend for odd mode suppression by hole array[J]. Chinese Journal of Radio Science, 2009，24(2): 228-232. (in Chinese)

[7] DAVIS M E, WILLIAMS E W, CELESTINI A C. Finite boundary corrections to the coplanar waveguide analysis [J]. IEEE Trans. on Microwave Theory and Techniques, 1973, 21(9): 594-596.

[8] FANG Shaojun, WANG Baisuo. Analysis of asymmetric coplanar waveguide with conductor backing[J]. IEEE Tran. on Microwave Theory and Techniques, 1999, 47(2): 238-240.

[9] 房少军. 非对称共面波导的特性及其场结构图的研究[D]. 辽宁 大连: 大连海事大学, 2001.