有孔腔体屏蔽效应分析的混合模型

张旭锋 李 颖 倪谷炎 罗建书

(国防科技大学理学院，湖南 长沙 410073)

1. 引 言

在电磁兼容领域，预测腔体屏蔽效应是经常遇到的一个问题。很多情况下，孔缝与屏蔽腔都是矩形的，因此，如何有效地评估带矩形孔缝的矩形腔屏蔽效应(SE)不仅具有很高的理论意义，而且具有实用价值。众多学者在腔体屏蔽分析方面作了大量工作，目前主要研究方法有：解析计算法，主要是Mendez用等效的电偶极子和磁偶极子来替代孔缝的方法[1]，Robinson提出的传输线法(TL)[2-4]，数值计算法，包括时域有限差分法(FDTD)[5]、矩量法(MOM)[6]、传输线矩阵法(TLM)[7]。Robinson提出的传输线法过程简单，计算速度快，且能分析参数对电磁屏蔽的影响，得到了广泛应用和发展。但是该方法只能计算腔体中心线上屏蔽效应，且只能分析垂直入射电场垂直于孔缝长边的情形。本文结合Robinson提出的传输线法与腔体并矢格林函数提出了一种用于估算带矩形孔缝的矩形腔屏蔽效应的解析方法，该方法能计算腔体内任意点屏蔽效应，并能分析入射角和极化角对屏蔽性能的影响。

2. 传输线/格林函数混合模型

如图1，为一平面电磁波照射到一带矩形孔缝的矩形腔，孔缝位于前板的中心，其中a、b、d为矩形腔长、宽、高，l、w为矩形孔缝长和宽。忽略通过腔体壁进入内部的能量，因此可以假设腔体壁是理想导体。根据Robinson提出的传输线模型[2],孔缝可以等效为一段两端短路的共面带状传输线,传输线的有效宽度为

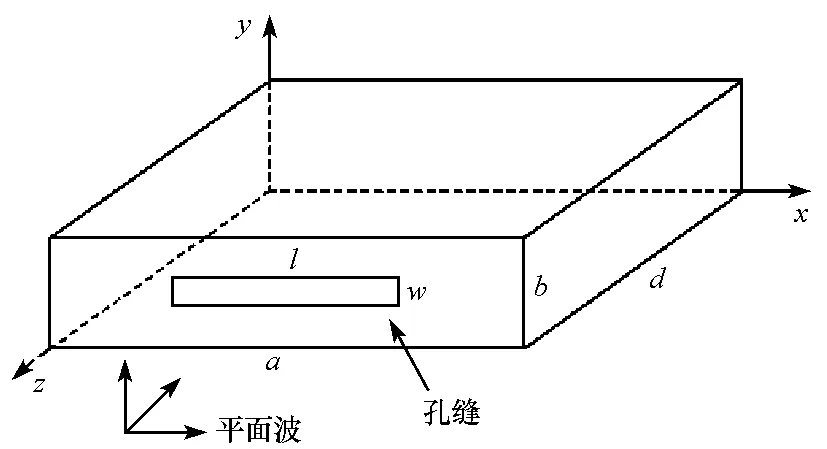
图1 平面入射波激励下的带孔缝矩形空腔

we=w-(5h/4π)(1+ln(4πw/h))

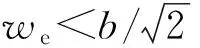
(1)

孔缝中心等效阻抗为

(2)

考虑平面波对传输线的耦合，传输线电报方程散射电压形式为[9](Agrawal模型)

(3)

式中

(4)

用格林函数法解方程(3)，电流和电压的格林函数为[10]

ρ2eγ(x>-l)](eγx<-ρ1e-γx<)

(5)

[e-γ(x>-l)+δρ2eγ(x>-l)]

(eγx<-δρ1e-γx<)

(6)

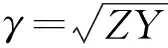
(7)

方程(3)的解为

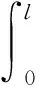
GI(x;l)V2

(8)

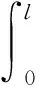
GV(x;0)V1+GV(x;l)V2

(9)

式中

(10)

(11)

传输线上总电压为

V(x) =Vsac(x)+Vinc(x)

(12)

屏蔽腔可等效为终端短路的波导,对TE10模，波导特性阻抗和传播常数为

(13)

(14)

式中，Z0，k0为自由空间波阻抗和传播常数。腔体在与孔缝连接处波导输入阻抗为

Zs=jZgtan(kgd)

(15)

平面波激励有孔屏蔽腔的等效电路如图2，从而可得波导输入电压为

Vin=V(x)Zs/(Zs+Zap)

(16)

由波导等效传输线中电压和电场的关系[11]

(17)

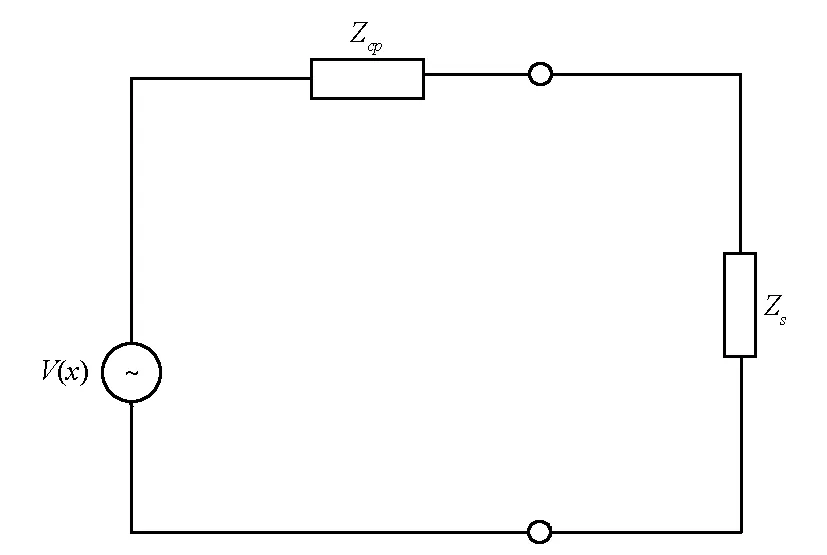
图2 平面波激励有孔屏蔽腔的等效电路

(18)

以M′=n×Eap(x)为等效磁流，利用腔体中并矢格林函数求解腔体中电磁场为

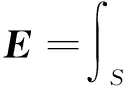
(19)

(20)

式中，GHM为矩形腔体中磁流源激励的磁型并矢格林函数[12]

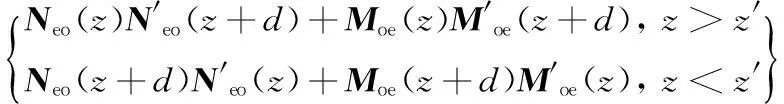
(21)

其中

(22)

(23)

(24)

矢量波函数为

Meo(z) =×(cos(kxx)cos(kyy)sin(kzz)z)

=kxsin(kxx)cos(kyy)sin(kzz)y-

kycos(kxx)sin(kyy)sin(kzz)x

(25)

Moe(z)=×(sin(kxx)sin(kyy)cos(kzz)z)

=kxsin(kxx)cos(kyy)cos(kzz)x-

kxcos(kxx)sin(kyy)cos(kzz)y

(26)

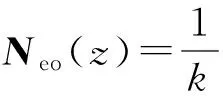
kzkycos(kxx)sin(kyy)cos(kzz)y+

(27)

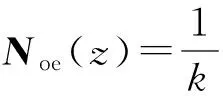
kzkysin(kxx)cos(kyy)sin(kzz)y+

(28)

作为近似计算，m、n取前几项计算，即可得到满意的结果。

腔体中某点的电场屏蔽效应定义为

SE=-20lg(|E/Einc|)

(29)

式中：E为腔体内观察点的场强；Einc为入射波场强。

3. 模型在孔缝偏离中心的扩展

对于孔缝偏离中心的情形，引入耦合系数Cm考虑腔体与缝隙的耦合[13-14]，只考虑TE10模，耦合系数为

(30)

式中：x1，xh，y1，yh为孔缝边界坐标；x0,y0为孔缝中心坐标。将式(2)中的阻抗替换为

(31)

利用前述的方法即可计算孔缝偏离中心时的屏蔽效应。

4. 算法有效性验证与分析

假设入射波为垂直入射的y-极化波(电场只有y分量)。屏蔽腔壁厚0.0015 m，腔体尺寸为0.3 m×0.12 m×0.3 m，带0.1 m×0.005 m矩形孔缝，图3实线为孔缝位于前板中心时，腔体中心点的电场屏蔽效应，与文献[2]和[11]中的测量值与计算结果吻合，验证了方法的有效性，结果表明，腔体谐振频率约为700 M，而谐振腔的TE101模谐振频率为707 M，两者基本相同，在谐振频率附近电场屏蔽效应显著下降。图3虚线为孔缝位于x0=0.2，y0=0.08，腔体中心点的电场屏蔽效应。与孔缝位于中心的情况相比较，腔体中心点的屏蔽效应有所增加，这是符合事实的。

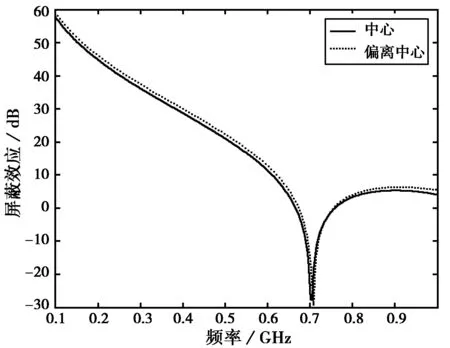
图3 孔缝位于不同位置的屏蔽效应

腔体尺寸为0.3 m×0.12 m×0.3 m，孔缝尺寸对腔体中心点的电场屏蔽效应影响如图4，显然，增大孔缝的尺寸会使屏蔽效应减小，孔缝长度增加会使谐振频率发生偏移和加宽，而孔缝宽度对谐振频率无影响，这主要是因为场的主模为TE101模，谐振频率与横向宽度无关。

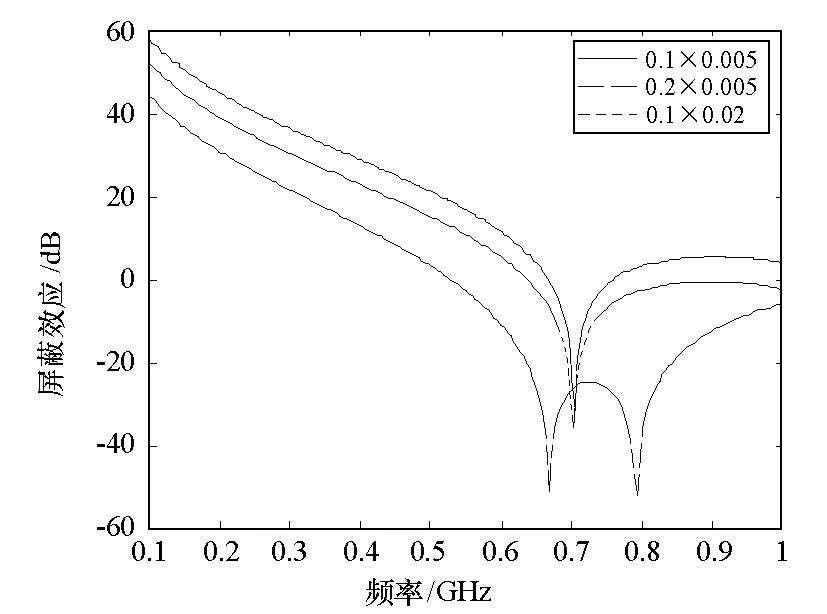
图4 不同尺寸孔缝的屏蔽效应

考虑平面波对孔缝的斜入射，假设k没有y分量，y与z夹角即为入射角。图5为700 M时，带0.1 m×0.005 m孔缝，0.3 m×0.12 m×0.3 m的腔体中心点屏蔽效应随入射角的变化。图6为屏蔽效应随极化角(E与y的夹角)的变化。注意到随入射角或极化角的增大屏蔽效应也增大，从而垂直入射y-极化波是屏蔽效应最差的情形。

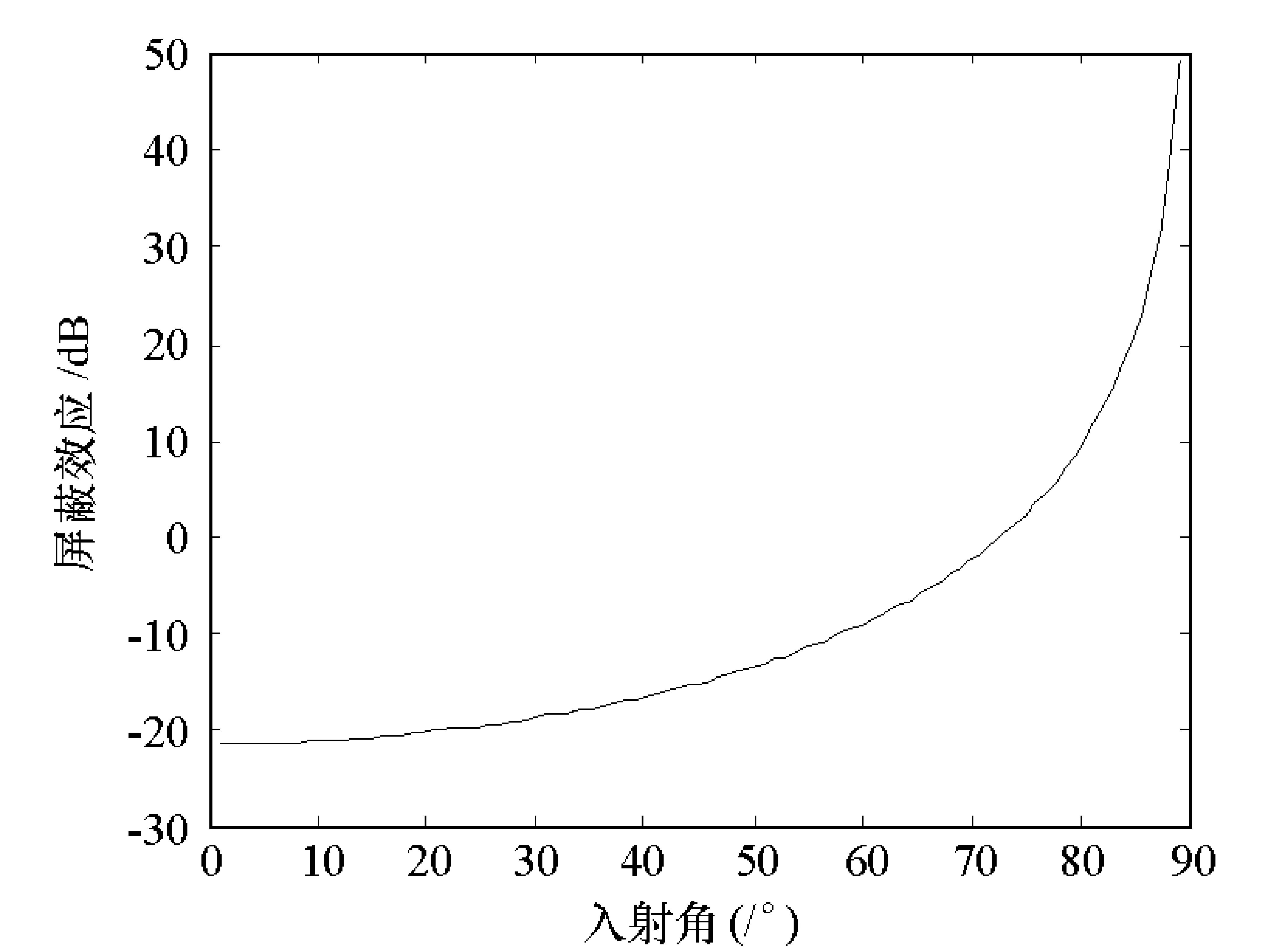
图5 屏蔽效应随入射角的变化

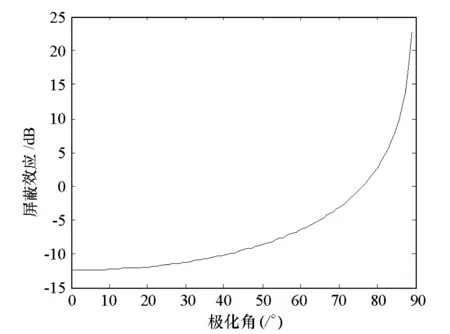
图6 屏蔽效应随极化角的变化

5. 结 论

利用传输线/格林函数混合法，分析了有孔矩形屏蔽腔体屏蔽效应，该方法应用平面波到传输线的耦合计算孔缝电压，然后利用矩形波导内电压与电场的关系求得孔缝上电场，并以此为等效磁流，计算腔体内的场分布。该方法具有较好的准确性和较小的计算量，不仅能分析腔体和孔缝参数对屏蔽效应的影响，也适用于任意入射和极化的电磁波，并能用于孔缝偏离板面中心的情形。

[1] MENDEZ H A. Shielding theory of enclosed with apertures[J]. IEEE Trans on Electromagnetic Compatibility, 1978, 20(2): 296-305.

[2] ROBINSON M P, BENSON T M, CHRISTOPOULOS C, et al. Analytical Formulation for the Shielding Effectiveness of Enclosures with Apertures[J]．IEEE Trans on Electromagnetic Compatibility, 1998, 40(8): 240-248.

[3] 汪柳平, 高攸纲, 沈远茂, 等. 装有PCB有孔矩形腔屏蔽效能的传输线法分析[J]. 电波科学学报, 2008, 23(4): 740-744.

WANG Liuping, GAO Yougang, SHEN Yuanmao, et al. Analysis of shielding effectiveness of rectangular cavity of loaded PCB with aperture by transmission line method[J]. Chinese Journal of Radio Science, 2009, 23(4): 740-744. (in Chinese)

[4] 汪柳平, 高攸纲. 有孔矩形腔的屏蔽效能及其对谐振抑制研究[J].电波科学学报, 2008, 23(3): 560-564.

WANG Liuping, GAO Yougang. Analysis of shielding effectiveness for rectangular cavity with apertures and resonance suppression [J]. Chinese Journal of Radio Science, 2008, 23(3): 560-564. (in Chinese)

[5] SARTO M S. FDTD Analysis of Field Penetration Inside the Composite Shells [C]// URSI International Symposium on Electromagnetic Theory, 1998: 674-676.

[6] CERRI G, LEO R D, PRIMIANI V M. Theoretical and experimental evaluation of the electromagnetic radiation from apertures in shielded enclosures[J]. IEEE Trans on Electromagnetic Compatibility, 1992, 34(11): 423-432.

[7] KRAFT C H. Modeling Leakage Through Finite Apertures with TLM [C]//IEEE International Symposium on Electromagnetic Compatibility, 1994: 73-76.

[8] GUPTA K C, GARG R, BAHI I J. Microstrip Lines and Slotlines [M]. Norwood, MA: Artech House, 1979.

[9] AGRAWAL A K. Transient response of multiconductor transmission line excited by a nonuniform electromagnetic field[J]. IEEE Trans. on Electromagnetic Compatibility, 1980, 22(2): 119-129.

[10] TESCHE F M, LANOZ M V, KARLSSON T. EMC分析方法与计算模型[M]. 吕英华, 王旭莹, 译. 北京: 北京邮电大学出版社, 2009.

[11] AZARO R, CAORSI S, DONELLI M, et al. A circuital approach to evaluating the electromagnetic field on rectangular apertures backed by rectangular cavities[J]. IEEE Trans on Microwave Theory And Techniques, 2002, 50(10): 2259-2266.

[12] YANG T. Coupling Onto Radio Frequency Components Enclosed Within Canonical Structures[D]. Michigan: University of Michigan, 2006.

[13] SHI Dan, SHEN Yuanmao, GAO Yougang. 3 high-order mode transmission line model of enclosure with off-center aperture[C]//IEEE International Symposium on Electromagnetic Compatibility, 2007: 361-364.

[14] 石 丹, 沈远茂, 高攸纲. 有孔屏蔽腔屏蔽效能的高次模分析[J].电波科学学报, 2009, 24(3): 510-513.

SHI Dan, SHEN Yuanmao, GAO Yougang. High-order modes analysis on shielding effectiveness of enclosure with off-center aperture[J]. Chinese Journal of Radio Science, 2009, 24(3): 510-513. (in Chinese)