新型坡度同轴布喇格反射器数值模拟比较研究
丁学用 王玲玲
(海南大学三亚学院理工分院,海南 三亚 572022)
1. 引 言
布喇格反射器被广泛应用于自由电子激光、回旋自谐振脉塞和半导体激光器中[1]。布喇格反射器由于其在集成电路、光波以及微波器件中的广泛应用,受到科技工程界的关注[1-13]。布喇格结构的周期性边界条件的选频特性所形成的禁带或者通带,可以用来制作反射器、滤波器、模式转换器等器件。例如,作为反射器,它是布喇格谐振腔的重要组成部分,被广泛应用在回旋自谐振脉塞(Cyclotron Auto-resonance Maser,CARM)和工作在毫米、亚毫米波范围内的自由电子激光(Free Electron Laser,FEL)[2-4]。通常,布喇格反射器是由一段在圆柱波导的金属壁上开周期性正弦或矩形波纹槽构成。近年来,由于同轴布喇格结构比传统的圆柱布喇格结构具有优越性,所以,越来越受到人们的重视[5-14]。对一种新型加坡度方式的同轴布喇格反射器进行理论与电磁仿真软件CST[15]数值模拟的比较研究,文中给出了理论编程和数值模拟比较结果,两者吻合较好,并对新型坡度同轴布喇格反射器的频率响应特性进行了理论研究。
2.理论模型
同轴布喇格反射器的结构[10]如图1所示,在纵向上呈周期性变化,其结构外半径Rout和内半径Rin可分别表示成关于纵向z变化的函数关系,且
Rout(z)=a0-loutcos(koutz+φout)
(1)
Rin(z)=b0-lincos(kinz+φin)
(2)
式中:kout=2π/pout;kin=2π/pin;a0、lout、φout、pout分别代表外导体壁的平均半径、开槽波纹深度、初始相位和波纹周期;b0、lin、φin、pin分别代表内导体壁的平均半径、开槽波纹深度、初始相位和波纹周期。

图1 同轴布喇格反射器的一般结构剖面图
对同轴布喇格结构的外导体内壁和内导体外壁加坡度有两种形式[16]:第1种形式是外壁加正坡度角、内壁加负坡度角,其剖面结构图和三维模型结构

(a)正圆锥形坡度
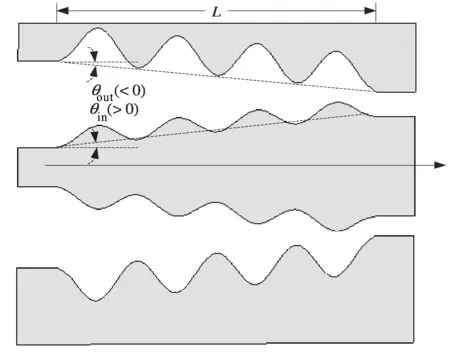
(b)倒圆锥形坡度图2 坡度开槽同轴布喇格反射器剖面图

(a)正圆锥形坡度

(b)倒圆锥形坡度图3 坡度开槽同轴布喇格反射器三维模型图
图如图2(a)、3(a)所示,称为正圆锥形坡度;第2种形式是外壁加负坡度角、内壁加正坡度角,其剖面结构图和三维模型结构图如图2(b)、3(b)所示,称为倒圆锥形坡度。内外壁倾斜的坡度角分别用θout和θin表示。本文中所加坡度方式与文献[16]不同,在文献[16]中,是将外导体内壁和内导体外壁分别绕一固定点旋转而成,在旋转点处极易形成奇点,会对布喇格反射器的性能有一定影响[17],而且加坡度后公式推导繁琐。在本文加坡度后的布喇格反射器中,其结构外半径Rout和内半径Rin可分别表示成关于纵向z变化的函数关系,且
Rout(z)=a0+tan(θout)z-
loutcos(koutz+φout)
(3)
Rin(z)=b0+tan(θin)z-
lincos(kinz+φin)
(4)
这为理论推导及软件编程提供了公式依据,且本文中加坡度前后布喇格反射器的结构长度L没发生变化。
假设同轴布喇格反射器中存在N种模式,根据同轴布喇格反射器多模耦合理论[18],其中第i模式(i=1,2,…,N)的沿z正方向传播的波(简称正传波)和沿z负方向传播的波(简称反传波),由下述耦合方程决定。
(5)
(6)

3.理论仿真模拟比较研究
根据同轴布喇格反射器多模耦合理论[18],利用一个中心频率为15 GHz,工作模式为TE11的同轴布喇格反射器[19],具体的结构参数如表1所示。
文中采用的研究方法是利用Fortran软件编程与CST软件平台进行理论模拟与非线性数值模拟。利用CST软件平台时,经过程序调试后,将软件的Lower mesh limit(结构线度上最低网格点数)设为10,Mesh line ratio limit设为12,总网格数达到3346560;为了减小总网格数,缩短仿真时间,在结构的XY平面设置了对称面(即磁对称面),并假设结构材料为理想导体[16]。
图4给出了多模耦合理论Fortran软件编程结果和CST软件模拟结果的对比。在图中布喇格反射器的内导体外壁与外导体内壁的波纹初始相位差分别为0,π/2和π。从图中可以看出,无坡度的同轴布喇格反射器,多模耦合理论Fortran软件编程与CST软件模拟得到的结果吻合。且当相位差为π时,同轴布喇格反射器获得最佳频率响应,最大反射系数接近1。在接下来的研究中,只考虑同轴布喇格反射器的内导体外壁与外导体内壁的波纹初始相位差为π的情况。
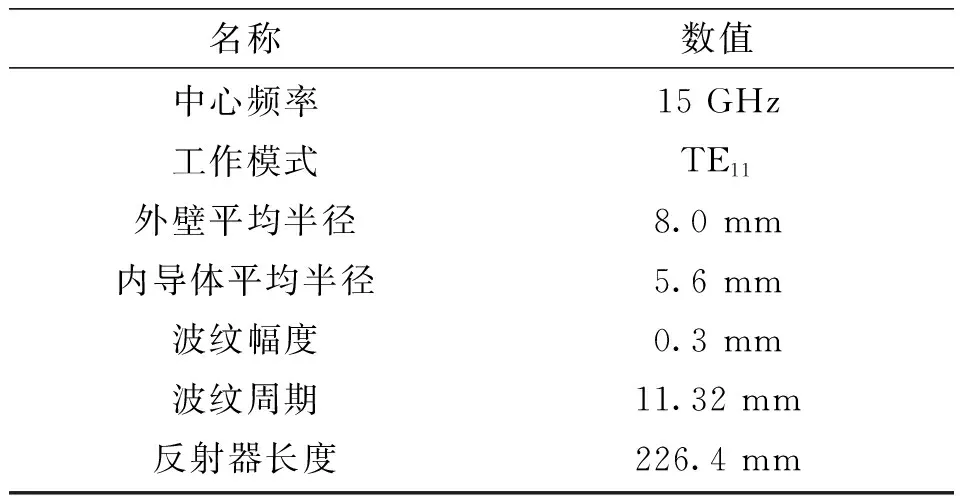
表1 15GHz 同轴布喇格反射器具体参数

(a)
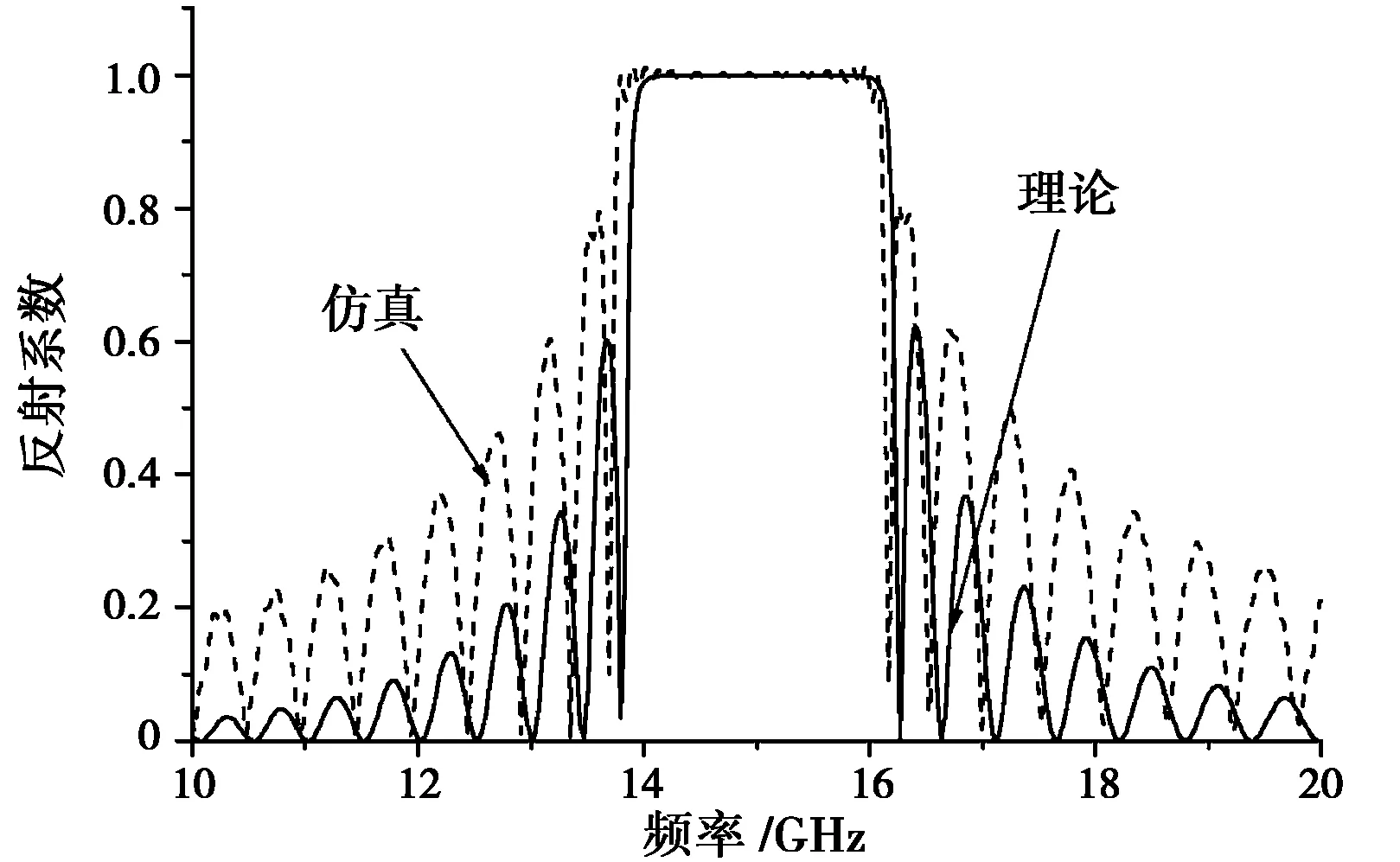
(b)

(c)图4 坡度角θout=0,θin=0时,多模耦合理论(Fortran软件编程)与CST软件结果的比较,初始相位为(a)φout=0,φin=0,(b)φout=0,φin=π/2和(c)φout=0,φin=π,pout=pin。其余参数示表1
图5中布喇格反射器的内导体外壁与外导体内壁波纹初始相位差为π且内外导体壁分别加有坡度。从图中可以看出,不管是正圆锥形坡度还是倒圆锥形坡度的同轴布喇格反射器,多模耦合理论Fortran软件编程和CST软件模拟得到的结果也同样吻合,两者存在些许偏差的原因可能是由于CST软件的一些参数(最小网格步长、最小网格点数、网格数等)的设置对仿真性能的影响。
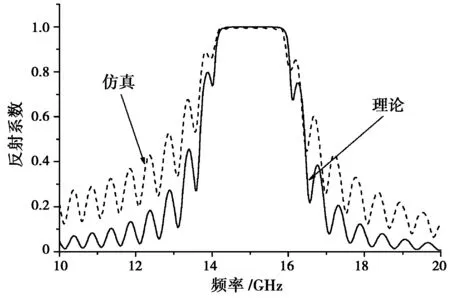
(a)

(b)图5 (a)正圆锥形下坡度角θout=0.5°,θin=-0.5° 和(b)倒圆锥形下坡度角θout=-0.1°,θin=0.1°时多模耦合理论(Fortran软件编程)与CST软件结果的比较,初始相位为φout=0,φin=π,pout=pin。其余参数示表1
在研究的过程中,发现CST软件仿真耗费的资源远远大于Fortran软件理论编程计算,并且不易处理高次模式间的耦合问题。理论编程计算整个过程耗时大约20分钟,内存占用较少,而CST软件仿真用了四个多小时,内存占用达到将近1 G,特别是高频率、高阶模式耦合时,CST需要增加很多网格,而多模耦合理论编写的程序可以容易的解决这个问题。
4.坡度对频率响应的影响
采用表1中典型参数,对具有新型坡度的同轴布喇格结构的频率响应特性,进行Frotran软件编程模拟研究。
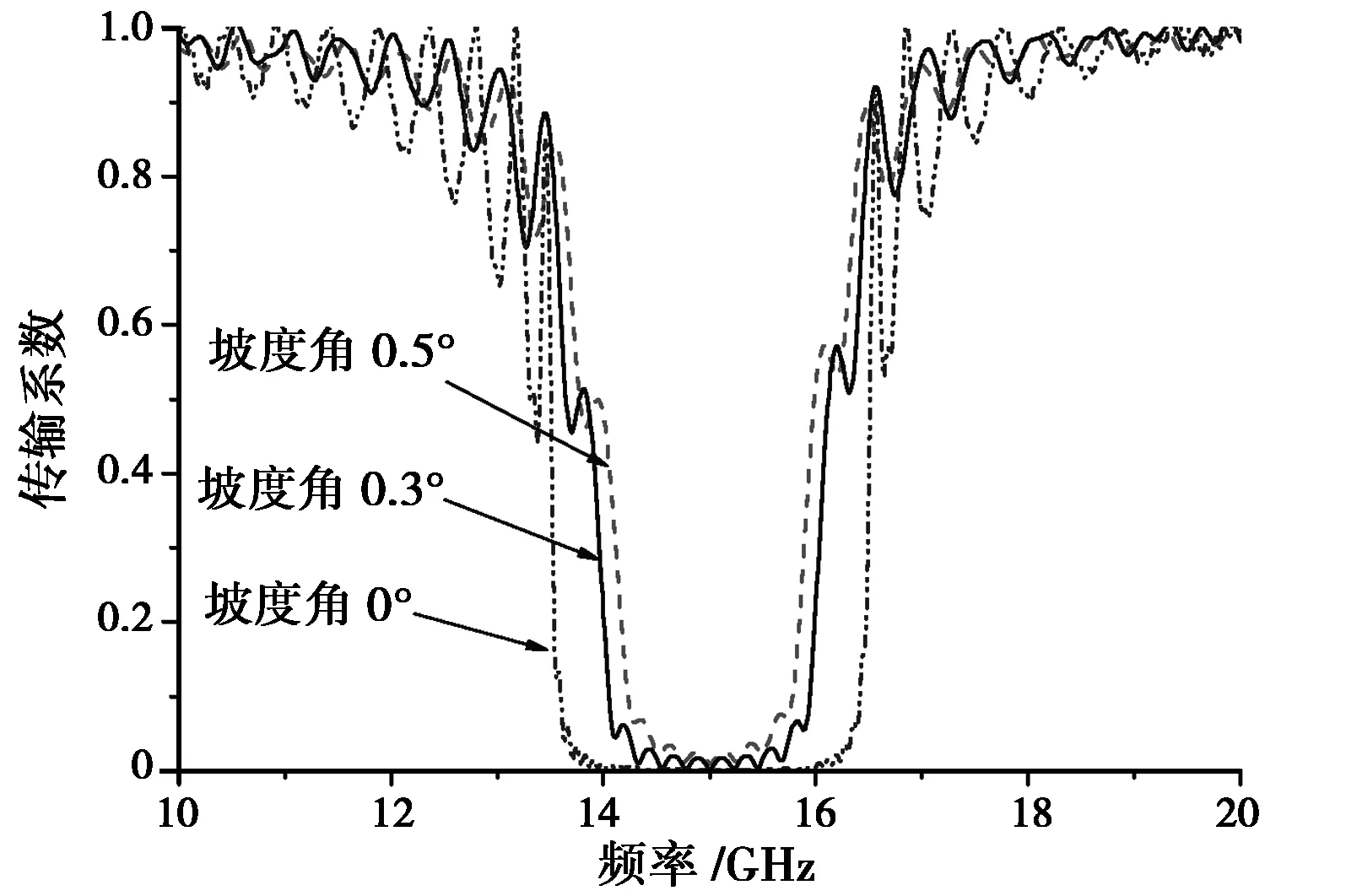
图6和图7是正圆锥形坡度和倒圆锥形坡度情况下所加不同坡度角时,反射系数和传输系数随频率的变化。从图中可看出:当对布喇格结构加正圆锥坡度时,其带宽随着所加坡度角的增大而变窄;当加倒圆锥形坡度时,其带宽随着所加坡度角的增大而变宽,而且加倒圆锥形坡度时,同轴布喇格反射器的频率响应受坡度角变化的影响较大。因此,如果需要获得较窄的带宽(例如用于布喇格反射器),可采取正圆锥坡度形式;如果需要获得较大的带宽(例如用于布喇格滤波器),则可采取倒圆锥形坡度形式。

(a)

(b)图6 同轴布喇格结构中TE11模的反射系数随频率的变化关系(Frotran软件编程),其中:(a)正圆锥形坡度下坡度角α=0°,0.3°,0.6°;(b)倒圆锥形坡度下坡度角α=0°,0.1°,0.2°,pout=pin,其余参数示表1
(a)

(b)图7 同轴布喇格结构中TE11模的传输系数随频率的变化关系,其中:(a)正圆锥形坡度下坡度角α=0°,0.3°,0.5°;(b)倒圆锥形坡度下坡度角α=0°,0.1°,0.15°,pout=pin,其余参数示表1

(a) 正圆锥形坡度
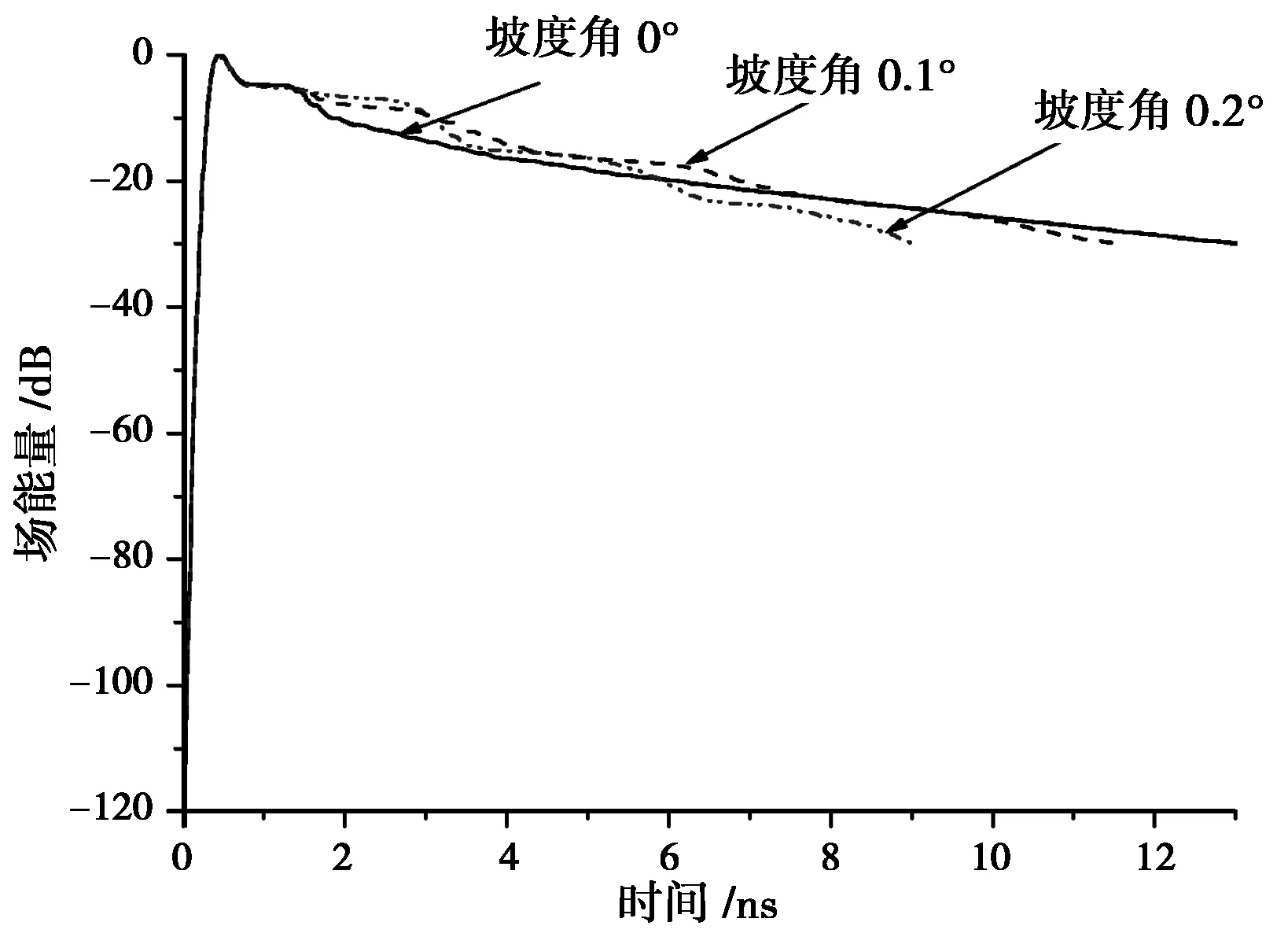
(b )倒圆锥形坡度图8 加坡度后能量衰减比较,参数示图6
图8是正圆锥形坡度和倒圆锥形坡度情况下所加不同坡度角时,场能量随时间的变化。从图中可看出,相比无坡度情况,加正圆锥形坡度后,能量衰减较快,并且随着坡度角的增大,能量衰减的速度也越快;加倒圆锥形坡度后,能量的衰减不是很明显,此时能量衰减受坡度角影响也较小。
5.残余旁瓣抑制
同样可以采用加窗技术来抑制加新型坡度的同轴布喇格反射器的残余旁瓣(residual side-lobes)现象[16]。设:
Rout(z)=a0+tan(θout)z-
loutW(z)cos(koutz+φout)
(7)
Rin(z)=b0+tan(θin)z-
linW(z)cos(kinz+φin)
(8)
式中,W(z)为窗函数。当W(z)=1,对应没有加载窗函数的情况,式(7)和(8)回复到式(3)和(4)。常用的汉宁(Hanning)窗、汉明(Hamming)窗、高斯(Gauss)窗以及布拉克曼(Blackman)窗的效果,彼此差别不大[16],本文仅讨论加载汉明(Hamming)窗函数
W(z)=0.54-0.46cos(2πz/L)
(9)
图9给出了新型坡度下具有正圆锥坡度反射器中坡度角α=0.3°时,不加窗和加载了汉明(Hamming)窗的对比。从图9可看出,加载汉明(Hamming)窗后频率响应曲线的残余旁瓣得到有效抑制。

图9 正圆锥坡度角α=0.3°时加载汉明窗函数对反射系数的频率响应曲线残余旁瓣的抑制作用(Fortran软件编程),此处所用其余参数与图6相同
加窗技术不仅可以提高布喇格反射器的性能,也可以减少仿真时间。因为用时域求解器求解时,傅立叶变换计算S参数要求时间信号完全衰减到零,否则就会引入截断误差。而布喇格反射器是高谐振器件,时间信号中可能会出现谐振,这使得信号的衰减非常缓慢,需要很长的仿真时间进行精确的傅立叶变换,而采用了加窗技术,在仿真时,瞬态场衰减到一定程度就会被傅立叶变换正确的截断而不产生很大的误差,又可以平滑通带。从图10可以看到,加窗后能量的衰减非常快,这样仿真所需要的时间也大大的减小。
图11是图6所示的正圆锥坡度(a)和倒圆锥坡度(b)结构在不同坡度角情况下,加载汉明(Hamming)窗后的效果。结果进一步表明:在新型加坡度方式下的同轴布喇格反射器,无论是正圆锥还是倒圆锥坡度,窗函数技术都能有效抑制频率响应曲线的残余旁瓣现象。

图10 加窗后能量衰减比较

(a)

(b)图11 对应图6(a)和(b)中参数,加载汉明(Hamming)窗函数后改善了的反射系数频率响应曲线
6.结 论
根据同轴布喇格反射器多模耦合理论,应用Fortran软件理论编程和电磁模拟软件CST对工作频率为15 GHz的同轴布喇格反射器进行了比较研究,发现多模耦合理论Fortran软件编程计算结果与CST软件模拟结果基本一致;与3维电磁软件相比,多模耦合理论编程容易,计算速度快,资源耗费少。并通过所进行的Fortran软件编程模拟结果,新型加坡度方式的坡度同轴布喇格反射器具有如下两个结论:
1) 具有正圆锥形坡度的同轴布喇格结构的带宽随着所加坡度角的增大而变窄;具有倒圆锥形坡度的同轴布喇格结构的带宽随着所加坡度角的增大而变宽。
2) 具有坡度的同轴布喇格反射器的频率响应残余旁瓣现象,也可以通过采用窗函数技术得到有效抑制。而且加窗技术可以减少软件模拟时间。
而且,新型加坡度方式的提出为以后研究坡度对高频高阶耦合模式下的同轴布喇格结构频率响应影响的理论推导提供了必要的理论依据。
[1] YARIV A and NAKAMURA M. Periodic structures for integrated optics[J]. IEEE J. Quantum Electronics, 1977, 13(4): 233-253.
[2] KOGELNIK H and SHANK C V. Coupled-wave theory of distributed feedback laser[J]. Appl. Phys., 1972, 43(5): 2327-2335.
[3] CHONG C K, MCDERMOTT D B, RAZEGHI M M, et al. Bragg reflectors[J]. IEEE Trans. on Plasma Sci., 1992, 20(3): 393-402.
[4] BARROSO J J and NETO J P L. Design of coaxial Bragg reflectors[J]. IEEE Trans. on Plasma Sci., 2006, 34(3): 666-672.
[5] KONOPLEV I V, MCGRANE P, CROSS A W, et al. Wave interference and band control in multiconductor one-dimensional Bragg structures [J]. Appl. Phys, 2005, 97(7): 073101-1-073101-7.
[6] 邓 峰, 赵正予, 张援农. 高频电波加热电离层对波传播影响的研究[J]. 电波科学学报, 2007, 22(6): 976-981.
DENG Feng, ZHAO Zhengyu, ZHANG Yuannong. Influence of HF heating on transmission of electromagnetic wave[J]. Chinese Journal of Radio Science, 2007, 22(6): 976-981. (in Chinese)
[7] KONOPLEV I V, MCGRANE P, PHELPS A D R, et al. Observation of photonic band-gap control in one-dimensional Bragg structures[J]. Appl. Phys. Lett. 2005, 87(12): 121104. doi: 10.1063/1.2043245.
[8] LAI Yingxin, ZHANG Shichang, ZHANG Huibo. A coaxial bragg reflector for cyclotron autoresonance maser oscillations[J]. IEEE Microwave and Wireless Components Letters, 2007, 17(5): 328-330. doi: 10.1109/LMWC.2007.895693.
[9] LAI Yingxin, ZHANG Shichang. Multiwave interaction formulation of a coaxial Bragg structure and its experimental verification[J]. Phys. Plasmas, 2007, 14(11): 113301. doi: 10.1063/1.2803767.
[10]ZHANG Shichang, CHEN Xiaohui, LAI Yingxin. Effect of eccentricity on transmission in a coaxial bragg structure[J]. Int. J. Infrared Millimeter Waves, 2007, 28(12): 1043-1050.
[11] LAI Yingxin,ZHANG Shichang. Separation of band-gap overlap in a coaxial Bragg structure operating in higher-order mode at Terahertz frequency[J]. Phys. Plasmas, 2008, 15(3): 033301.
[12] CHEN Xiaohui, ZHANG Shichang, LAI Yingxin. Suppression of residual side-lobes in a coaxial Bragg reflector[J]. Int. J. Infrared Millimeter Waves, 2008, 29(6): 552-557.
[13] PRETTEREBNER J and THUMM M. Design of improved Bragg reflectorsfor resonators in over-moded high-power microwave oscillators[C]//Dig.Infrared and Millimeter Wave Conf., SPIE 1514, 1990: 298-300.
[14] CST. Microwave Studio[M]. 4th ed.Computer Simulation Technology, 2002.
[15] 丁学用, 张世昌, 谢永超. 具有坡度的同轴布喇格结构的频率响应特性[J]. 强激光与粒子束, 2008, 20(12): 2051-2054.
DING Xueyong, ZHANG Shichang, XIE Yongchao. Characteristics of frequency response in a coaxial Bragg structure with tapered ripples[J].High power laser and Partical Beams, 2008, 20(12): 2051-2054. (in Chinese)
[16]DING Xueyong, ZHANG Shichang. Comparative study of tapered coaxial Bragg structure with various ripples[J]. Journal of Physics D: Applied Physics, 2009, 42(8): 085104.
[17] LAI Yingxin, ZHANG Shichang. Multi-mode coupling in a coaxial Bragg reflector[OL]. [2007-4-29]http://www.paper.edu.cn/index.php/default/en_releasepaper/content/13787.
[18] CHEN Xiaohui, LAI Yingxin, ZHANG Shichang. Comparative study of a 15 GHz coaxial Bragg reflector[C]//The 2008 Global Symposium on Millimeter Waves Proceeding, 2008: 369-371.

