一个关于函数不等式约束优化问题的算法

迟晓燕

（重庆师范大学数学学院，重庆 401331）

1 问题引入

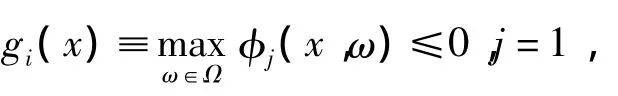
2 问题近似

首先对函数不等式约束，应用与Jennings和Teo（1990）［1］相同的约束转换.对每一个j=1，2，…，m，定义:

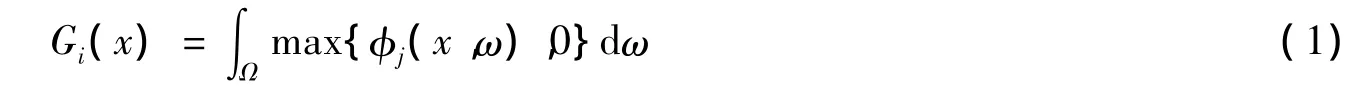
因为φj关于x和ω是连续可微的，max{φj（x，ω），0}是ω的连续函数，∀x∈Rn，所以函数约束等价于:

方便起见，令问题（P）也定义为f（x）关于式（2）的极小化问题.令F为问题（P）可行域，定义:

进而，令int（F）定义为F的内部，即

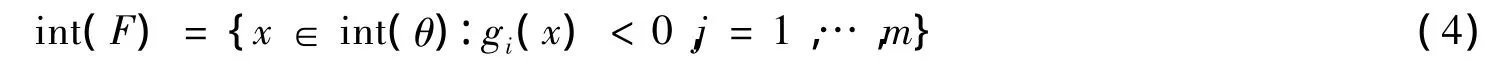
接下来给出如下假设:

1）int（F）≠Ø;2）对问题（P）的最优解x*，存在一个参数向量∈int（F），使得α+（1－α）x*∈int（F），∀α∈［0，1］.

一般来讲，对每个j=1，…，m，Gj（x）在x处是光滑的，因此，标准优化方法来解这类等式约束是有一定困难的.下面采用光滑方法，用gi，ε（x，ω）来取代max{φj（x，ω），0}.

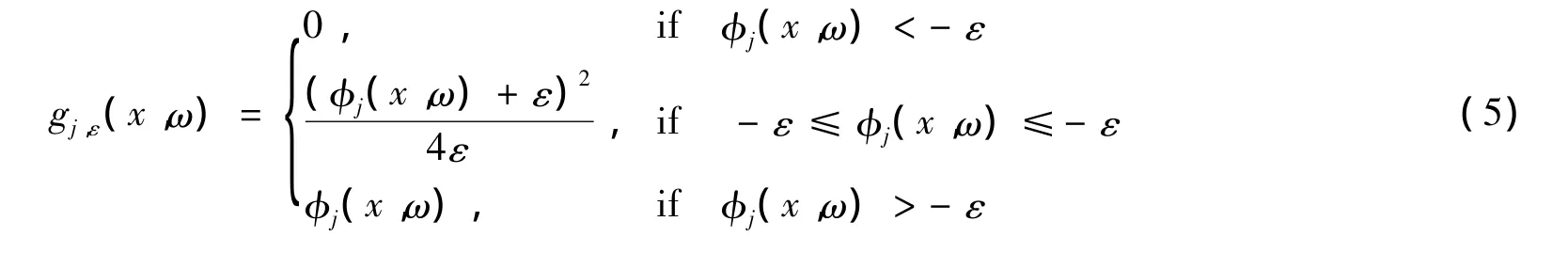
这种光滑化方法在以前的文章中已被采用过.对每个j=1，…，m，定义:

对任意j=1，…，m，gj，ε（x，ω）关于x是连续可微的.令:

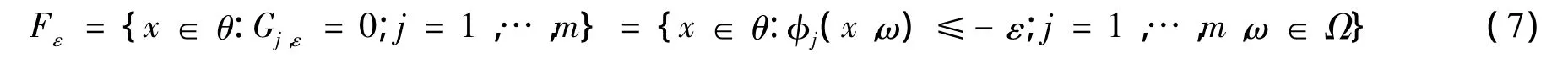
易知:Fε⊂F，∀ε ＞0.

现在定义一个近似问题（Pε，γ）.∀γ ＞0，X∈θ，最小化费用函数:

以下结果保证了（Pε，γ）关于（P）的解的可行性.

定理 1 ∃γ（ε）＞0［2］，使得对所有 γ ＞γ（ε），对问题（Pε，γ）的任何解也是问题（P）的可行点.

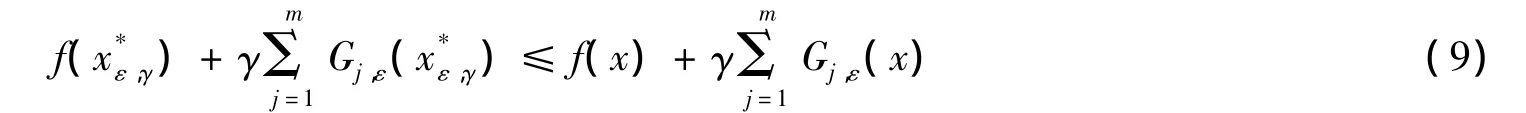
对所有x∈θ，固定xε∈Fε，由Gj，ε定义知，Gj，ε=0;j=1，…，m.因为 θ为紧的且f为连续的，存在一个∈θ，使得f¯）≤f（x），∀x∈θ.易知两边同时增加罚条件［3］，由xε定义和式（9）可得:

整理得:

令z=f（xε）－f（¯），则式（11）变形为

Jennings和 Teo已经给出了证明:∀ε，∃τ（ε），使得对所有 0 ＜ τ ＜ τ（ε），如果Gj，ε（x）＜ τ，则x∈F.因

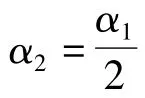
3 算法

基于前面两个结论，给出解决问题（P）的算法.

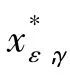
4 数值计算

以简单的边界形式给出普通等式约束［5］，0≤x1≤100，0.1 ＜x2≤100，0≤x3≤100.

应用以上算法，给出如下结果（表1）:

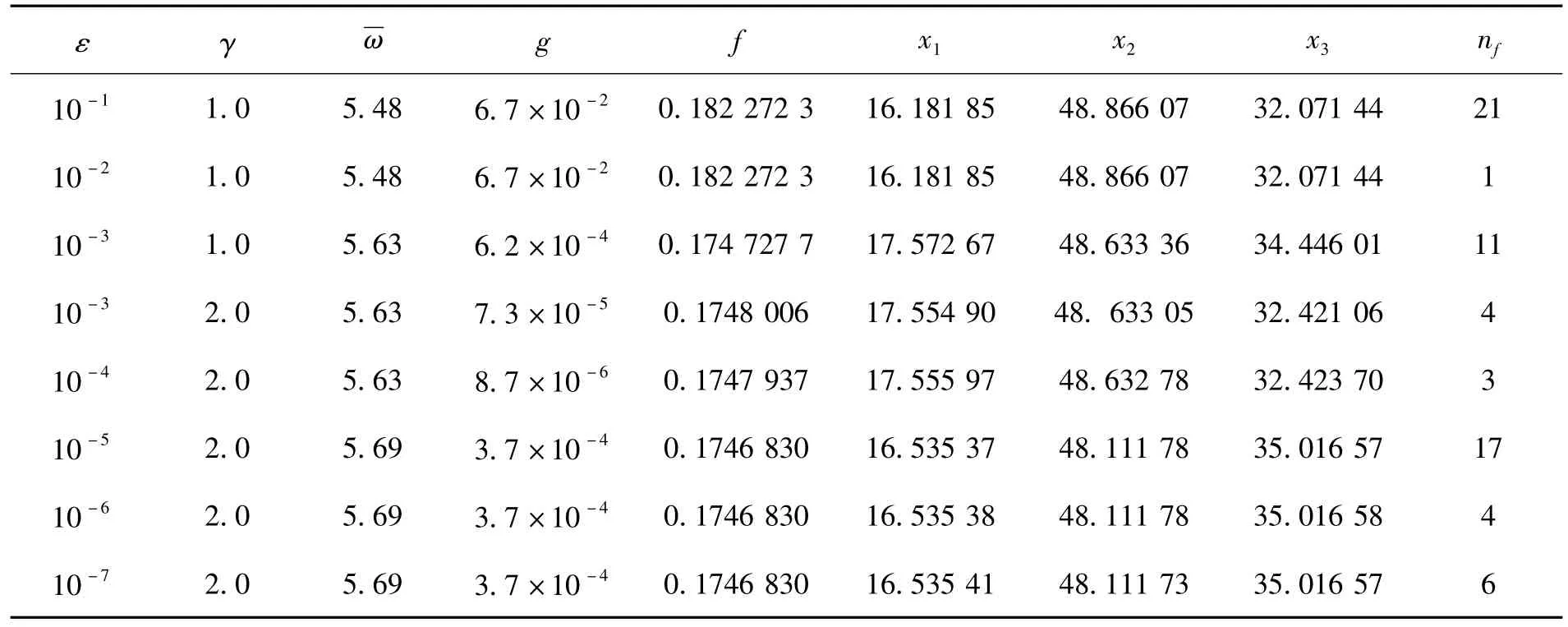
表1 计算结果

［1］JENNINGS L S，TEO K L.A computational algorithm for functional inequality constrained optimization problem［J］.Automatica，1990，126（2）:371-375

［2］BERTSKAS D P.Constrained Optimization and Lagrange Multiplier Methods［M］.New York:Academic Press，1982

［3］BURKE J V.An exact penalization viewpoint of constrained optimization［J］.SIAM J.Control and Optimization，1991.29:968-998

［4］曾波，龙茜.无约束最大子序列求和改进算法［J］.重庆工商大学学:自然科学版，2007，24（6）:600-602

［5］LUENBURGER D G.Linear and Nonlinear Programming［M］.New York:Addison-Wesley，1984