一类平面图的强边着色

薄朝升，谢德政

（重庆大学数学与统计学院，重庆 401331）

考虑的图均为无向简单有限图.图G的强边着色是正常边着色且任何长为3的路的边不着双色.图G的强边色数是G的所有强边着色中使用色数的最小者，记为χ's（G）.

Erdös和 Nestril［1］提出以下猜想（强边着色猜想）:对任意图G，

对于 Δ =3 的图，强边着色猜想已被证明［2，3］.Horak［4］证明了对于 Δ =4 的图，χ's（G）≤23;Cranston［5］利用时间序列算法证明了对于Δ=4的图，χ's（G）≤22.

度为k的点称为k－点;度不小于k的点称为k+－点.设p是一条长为k+1的路，且其所有的内点（一

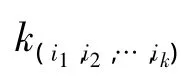
定理1 设图G是平面图且满足g（G）≥14，则

设图G是一个满足定理条件且含有最少边的反例（Δ≥3）.则对于G有以下断言成立:

断言1G不含有1－点.

图1 G

断言2G不含有2（1，1）－点.

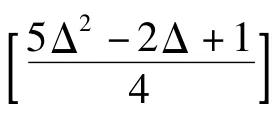
断言 3G不含有 3（1，2，2）－点.

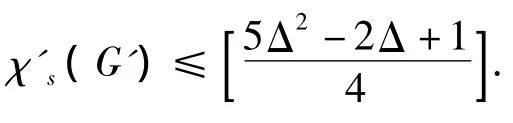
1{c（uv1），c（uw1）}，要对uu1着色，需避开c（x）∪c（v1）∪c（w1）中的颜色.而|c（x）∪c（v1）∪c（w1）|≤2Δ +1，故至少有3种颜色可用于对uu1的着色，从而完成了对G的一个强边着色，矛盾.若c（u1x）∈{c（uv1），c（uw1）}，不妨设c（u1x）=c（uv1）=c.首先对uv1重新着色，只需避开c（v2）∪c（w1）∪{c}中的颜色，显然，存在颜色c'可用于对uv1的重新着色，且使得c（u1x）{c'（uv1），c（uw1）}.从而，与上面类似，可完成对G的一个强边着色，矛盾.

综上，极小反例G不包含断言1－3的构图.

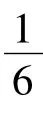
现在按照法则R1和R2，对G中的任意点重新赋值，设新的赋值函数为ch'，则有以下情况:情况1u是一个2－点.

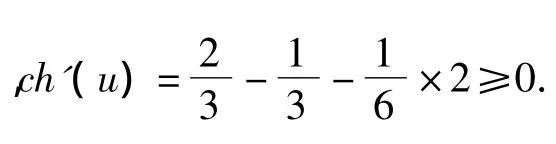
情况3u是一个4+－点.

［1］ERDOS P，NESETRIL J.Problem.In:G.Halsz and V.T.Sos，Editors，Irregularities of Partitions［M］.New York:Springer，1989

［2］ANDERSEN L A.The strong chromatic index of a cubic graph is at most 10 ［J］.Discrete Math，1992，108（1－3）:231－252

［3］HORAK P，QING H，TROTTER W T.Induced matching in cubic graphs［J］.J Graph Theory，1993，17:151－160

［4］HORAK P.The strong chromatic index of graphs with maximum degree four［J］.Conterp Methods Graphs Theory，1990（8）:399－403

［5］CRANSTON C.Strong edge－coloring of graphs with maximum degree 4 using 22 colors［J］.Discrete Math，2006，306:2772－2778

［6］MONTASSIER M，OCHEM P，RASPAUD A.On the acyclic choosability of graphs［J］.J Graph Theory，2006，51:281－300

［7］BONDY J A，MURTY U S R.Graph Theory［M］.Berlin:Springer，2008

［8］张卫标，杨清军.关于强边着色猜想的最优图问题［J］.重庆工学院学报，2009，26（6）:538－547