基于出生性别比例的逻辑斯谛人口模型的混沌性质*

李艳午，周基燕，吴翠萍

（1.芜湖信息技术职业学院，安徽芜湖241000;2.南京大学 社会学院，南京210093;3.安徽师范大学 社会学院，安徽芜湖 241000）

国际上一般以每出生100个女性人口相对应出生的男性人口的数值来表示出生人口的性别比例［1］。绝大多数国家的人口生育史表明，在不进行人为控制的情况下，新生婴儿的性别比应保持在102～107［2］之间。这是由人类生殖过程的生物学特性决定的。对这个数值的任何人为控制和改变，都会对人口的两性结构造成严重危害，带来人口安全的隐患。

人口安全问题关乎社会的稳定与和谐，关乎一个国家的正常发展。我国计划生育政策的实行，以及历来重男轻女思想的影响，导致我国出生人口的性别比例严重失衡，目前出生人口性别比例近似118.59［3］。根据混沌理论的“初值敏感度”理论，出生性别比例的失衡必将导致人口发展在一定程度上背离正常的轨道，从而带来一系列的社会问题。

此处针对我国出生人口性别比例严重失衡的现状，建立了基于出生人口性别比例的逻辑斯谛人口模型，改进了原来的逻辑斯谛人口模型，并研究了这种改进模型的混沌性质，旨在提醒人们出生人口性别比例的失衡将导致人口变化规律杂乱无章，人口结构趋于畸形的后果。

1 逻辑斯谛人口模型

约定:P0表示初始人口数量;P表示n年以后的人口数量;n表示时间（年）;r表示人口的增长率;M表示人口的饱和容量，即一定的社会资源所能供给的最大人口数量。

在一个现实的人口增长模型里，人口的增长率r本身常常随着人口数量的变化而变化，有时候会因为人口数量的庞大而在一定时期内呈负数。例如:当人口数量庞大到饱和容量的时候，社会资源供给的能源开始减少，走向枯竭，人口数量必然减少，这就如同澳洲大草原上狼与兔子的数量总是此消彼长。

改进成了逻辑斯谛模型［4］:

根据逻辑斯谛人口模型，当初始人口数量P0小于人口的饱和容量M时，P＞P0，人口数量呈正增长;当初始人口数量P0大于人口的饱和容量M时，P＜P0，人口数量呈负增长。

逻辑斯谛人口模型改进了马尔萨斯人口模型，在一定程度上能较为客观地描述人口增长的规律。但是，人口变化的规律是极其复杂的，往往受人口的群体结构（性别比例、年龄结构、知识结构）和环境（迁移、战争、自然灾害）等因素的影响。所以，逻辑斯谛模型也并不是描述人口变化规律的理想模型。

2 基于出生性别比例的逻辑斯谛人口模型

从全国情况看，20世纪80年代中期以来，我国新出生人口的性别比就开始迅速攀升。人口普查资料显示，1981年全国出生婴儿性别比是108.47，1989年这个数字就达到了111.92，2000年第5次人口普查公布数字更是高达116，远远超过国际通用可以容忍的最高警戒线107。社会学们已经讨论了出生人口性比例失衡带来的种种社会危害，这里要讨论的是这种失衡对人口变化规律的影响。

出生人口性别比例严重失衡直接影响到人口的出生率。根据一个国家制定的人口政策，假设出生率定为r，而事实上，由于出生性别比例比较大，就意味着有一部分人不可能结婚生育，从而出生率肯定低于r，必须对r作一个修正，建立新的模型，才能比较准确地反映人口变化的规律。

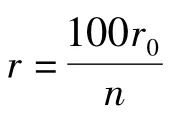
这是一个迭代:

3 混沌性质

对于模型（2），有没有一个不动点Pn，使得Pn=Pn+1.因为，这时候意味着人口从此以后不增也不减，进入稳定期，当然这是一种理想的状态。令:

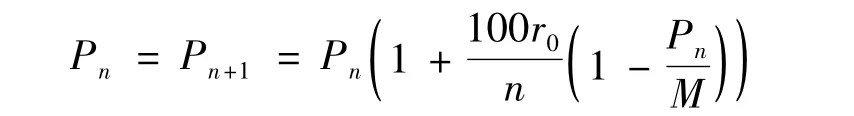
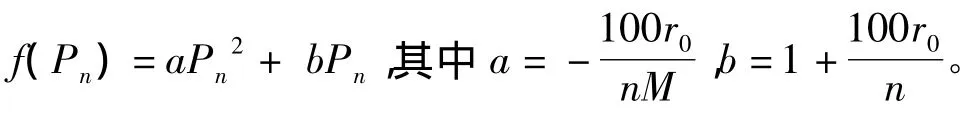
（1）当－1＜a＜0，b=a时，只有一个不动点Pn=0。

（2）当－3＜a＜－1，b=a时，有两个不动点:Pn=0与Pn=M。事实上，Pn=M是稳定的不动点，而Pn=0是不稳定的不动点，因为在零点附近任取Pn的值进行迭代，最终的结果都趋向于M。

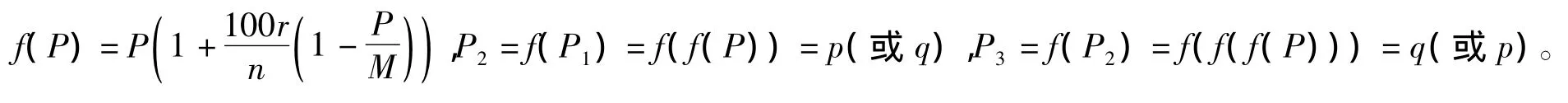
从此以后出现迭代循环…p→q→p→q→…，于是p，q就是迭代函数f（Pn）的周期点，这里的周期为2，所以又叫双周期点，这种现象称为周期倍化现象［6］。

进一步地，当a再变小些时，迭代函数f（Pn）两个周期点又分化成4个;随着a的慢慢变小，迭代函数f（Pn）的周期点的个数会不断增加，将出现8个周期点，16个周期点，最后通过计算机计算可知，当a无限靠近－3.569 945 971 8的时候，将出现无穷多个周期点。而无节制的周期倍化现象正是混沌现象的特征之一［7］，这表明迭代函数的变化进入了混沌状态。

4 结论

从上面的讨论可以看到，即使a的变化范围不算大，都会导致迭代函数迅速进入混沌状态。这就表明当M和r0一定的时候，出生人口的性别比例n将成为决定人口变化规律的敏感因素。n的非正常性将直接导致人口变化的无规律性，即混沌性质。

在对迭代函数混沌性质的讨论过程中，为了简化，只在b=a的特殊情况下对a的不同取值范围进行讨论。事实上，可以在两个参数a和b的不同取值范围内来讨论。

［1］邬苍萍.世界人口［M］.北京:中国人民大学出版社，1983

［2］潘纪一.世界人口通论［M］.北京:中国人口出版社，1991

［3］刘仕海.中国人口性别比例失调的文化人类学思考［J］.西北第二民族学院学报:哲学社会科学版，2006，18（2）:28-30

［4］李鸥.人口出生性别比例问题研究［J］.天津行政学院学报，2004，5（4）:71-74

［5］黄润生，黄浩.混沌及其应用［M］.武汉:武汉大学出版社，2005

［6］吴祥兴，陈忠.混沌学导论［M］.上海:上海科学文献出版社，2001

［7］刘仕达.自然科学中的混沌和分形［M］.北京:北京大学出版社，2004

［8］陈友华.中国人口现代化发展的历史与现状［J］.人口学刊，2005（2）:30-34

［9］陈友华.孩次递进比数学模型的建立与生育表的构造［J］.中国人口科学，1993（3）:58-63