区间数Fuzzy集的一种模式识别方法*
夏昊冉,胡永培
(安徽大学数学科学学院,合肥 230039)
Fuzzy逻辑是一门崭新的数学分支,它始于1965年美国自动控制论专家L.A.Iadeh的开创性论文“Fuzzy集合”.凭借Fuzzy集中的隶属原则和贴近原则,人们能够对问题做出较准确的评判和决策.但事物的特征信息存在着复杂性、模糊性和不确定性,如:一个测验,80分到90分为等级“良”,70分到80分为等级“中等”,一个考试估计分数在77分到82分之间,那么这个考生的成绩可能为什么等级,正如这样,得到的数据并非是一个确定的信息,而是一个区间或一个范围.针对这种情形,有学者提出了建立区间数Fuzzy集[1],文献[2]给出一种区间数Fuzzy集的隶属原则,并介绍了一种模式识别的方法.郭春香,郭耀煌[3]提出格序决策理论,对区间数Fuzzy集做了研究.运用区间数Fuzzy集解决模糊综合评价的文献更是很多,比如文献[4][5].
此处基于区间数Fuzzy集知识,对文献[3]提出的“偏好距离”进行简化,并在贴近度的基础上,提出贴近区间概念,给出了一种新的区间数Fuzzy集模式识别方法,实例证明了该方法的可靠性和有效性.
1 预备知识
定义1 设A=[a-,a+]={x|a-≤x≤a+},称A为区间数;若a-=a+,则称A为退化区间数;若0A,称A为无零区间数;若A=[0,1],则称A为单位闭区间,记作I.
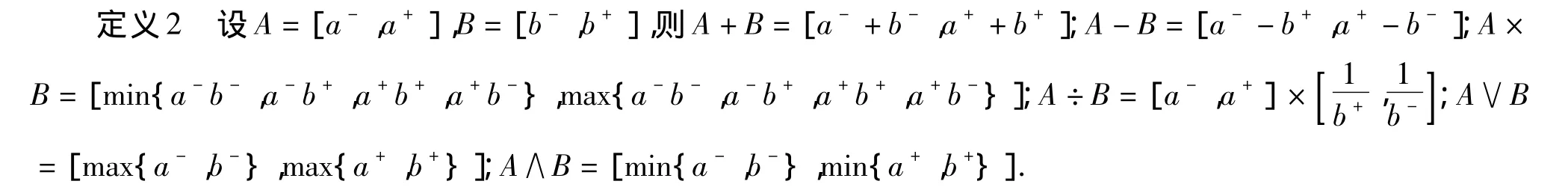
定义3 设X为非空普通集合,称映射f:X→[I]为X上的区间数Fuzzy集.X上所有的区间数Fuzzy集记为IF(X);论域U上所有区间数Fuzzy子集构成的子集称为区间数Fuzzy幂集,记作IF(U).
2 区间数Fuzzy集的序
根据文献[6]中的偏序概念,可以推出如下定理.
定理1 若P是一个区间数集合,∀A=[a-,a+],B=[b-,b+]∈P,称P为一个偏序集,满足:A≤B⇔a-≤b-,a+≤b+.
从自反性、反对称性、传递性三方面容易验证.
3 区间数上的距离
可以根据实数上距离的定义,给出区间数上的距离,如下:
定理2 设A=[a-,a+],B=[b-,b+],则区间A与区间B的距离可以定义为d(A,B)=|a--b-|+|a+-b+|.显然,这个距离的定义同样满足非负性、自反性和三角不等式.
文献[3]通过与两区间数的拟上下确界比较,计算其之间的“偏好距离”,得出这两个区间的“序关系”.此处提出如下定理,无须求其拟上下确界,简化了文献[3]中所提及的方法,但仍可以得到相同的结论.
首先,假设这两个区间是不具备定理1条件的“偏序关系”,否则“序关系”已经确定.
即对图1的b情况做讨论.
定理3 对于不满足定理1的两区间A=[a-,a+],B=[b-,b+],C为区间A,B的拟下(上)确界[3];D=[d-,d+]为任意一个满足序关系D≤A,D≤B(A≤D,B≤D)的区间,则d(A,B)和d(B,C)的大小关系与d(A,D)和d(B,D)的大小关系相一致.
证明 不妨设a-≤b-,a+≥b+,C为A,B的拟下确界,则C=[a-,b+],d-≤a-,d+≤a+;d-≤b-,d+≤b+;d(A,C)=|a--a-|+|a+-b+|=a+-b+;d(B,C)=|b--a-|+|b+-b+|=b--a-.所以d(A,C)-d(B,C)=(a++a-)-(b++b-).同理d(A,D)-d(B,D)=(a++a-)-(b++b-),所以d(A,C)-d(B,C)=d(A,D)-d(B,D).即d(A,B)和d(B,C)的大小关系与d(A,D)和d(B,D)的大小关系相一致.
该定理说明,在求区间数的序关系时,对于不具备偏序关系的区间,只需利用距离定义,与某一“基准”比较即可.“基准”可以是拟上、下确界,也可以是其他区间.
实例1 (数据来自于文献[3])

图1 两区间关系图示
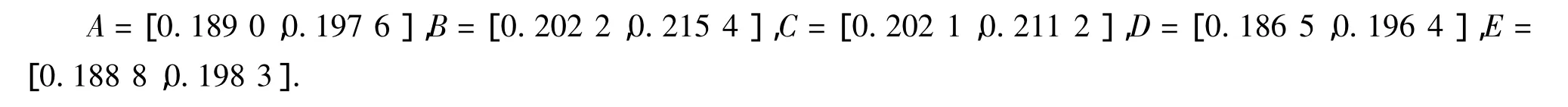
以D为基准,利用定理3,得d(D,A)=0.003 7,d(D,E)=0.004 2,所以d(D,A)<d(D,E),也就是A离E较近.有理由认为D<A<E<C<B,其判断结果与文献[3]相同.
注:若d(D,A)=d(D,E),可以认为A=E.
4 贴近原则
定义4 设A,B是论域U的区间数Fuzzy子集,则A,B交集A∩B,A,B并集A∪B,A,B的包含关系定义如下:

定义5 设A∈IF(U),有:
(1)HgtA=[maxA-(x),maxA+(x)],x∈U叫区间数 Fuzzy集A的高度区间.
(2)DpnA=[minA-(x),minA+(x)],x∈U叫区间数 Fuzzy集A的低度区间.
定义6(贴近区间)设对于每对A,B∈IF(U),有区间q(A,B)对应,满足:
(1)[0,0]≤q(A,B)≤[1,1];(2)q(A,B)=q(B,A);(3)A⊆B⊆C时,q(A,C)≤q(A,B).
存在q(B,C),则称q为IF(U)中贴近区间,称q(A,B)为区间数Fuzzy集A与B的贴近区间.
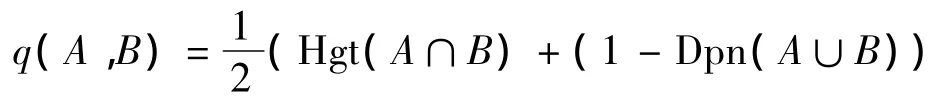
证明
(1)显然[0,0]≤Hgt(A∩B)≤[1,1],[0,0]≤Dpn(A∪B)≤[1,1],则[0,0]≤q(A,B)≤[1,1].
(2)q(A,B)=q(B,A),显然.
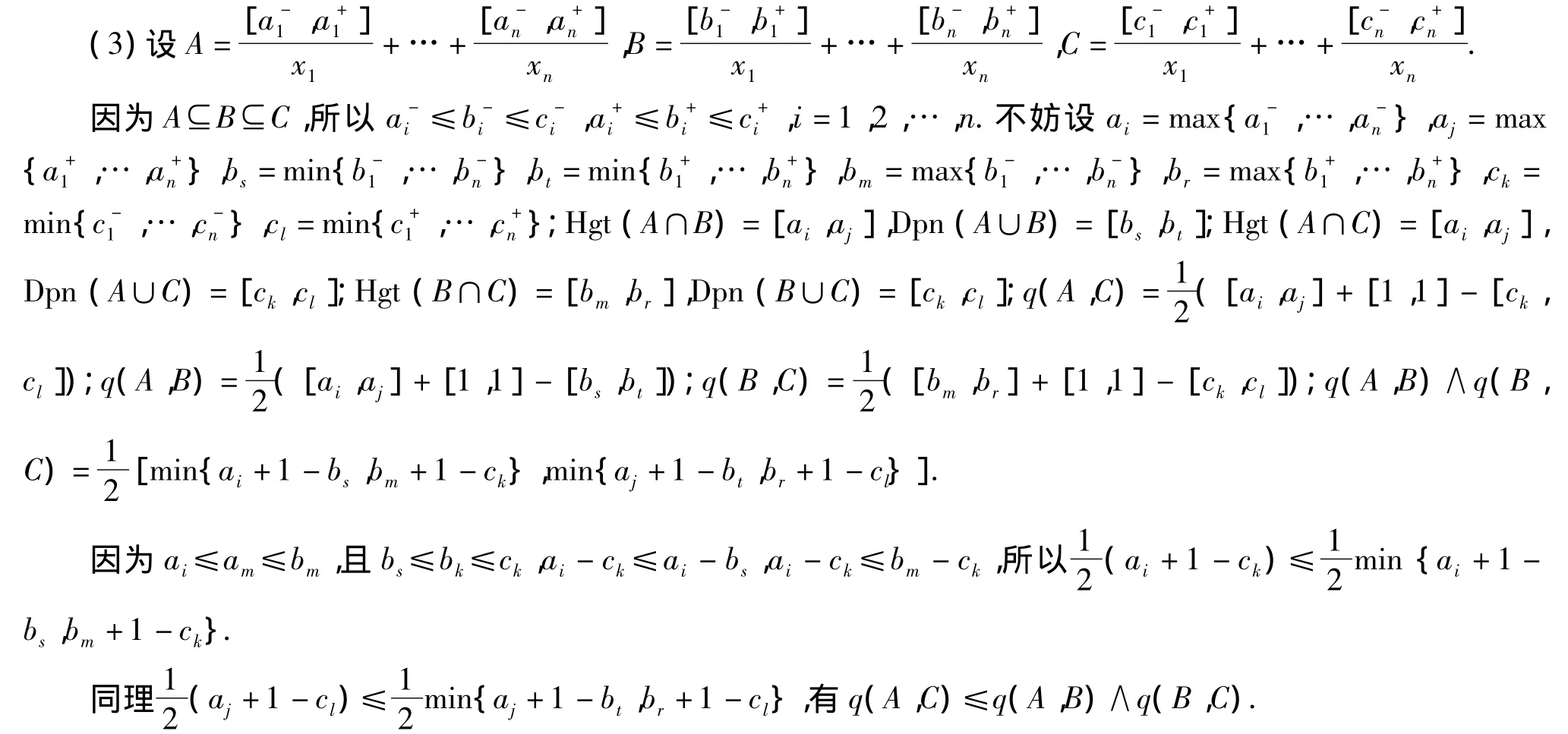

实例2 设一个目标跟踪系统有5个区间数Fuzzy模式(表1),现在有1个目标A*:
A*=([0.402,0.412],[0.2,0.221],[0.102,0.135],[0.385,0.421],[0.428,0.472],[0.521,0.552]),那么A*可能属于A1,A2,A3,A4,A5中哪个模式?

表1 目标跟踪系统的区间Fuzzy模式
解 运用定理4 算法,得出q(A*,A1)=[0.541,0.585],q(A*,A2)=[0.535,0.595],q(A*,A3)=[0.5,0.515],q(A*,A4)=[0.451,0.4825],q(A*,A5)=[0.4825,0.509].则:
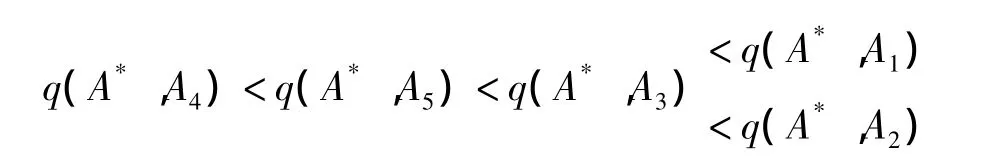
因为d(q(A*,A1),q(A*,A3))<d(q(A*,A2),q(A*,A3)),所以A*与A2最为贴近,所以可以把A*归为模式A2.
[1]GORZALCZALCZANY M B.A method of inference in in approximate reasoning based on interval—valued fuzzy sets[J].Fuzzy Sets and Systems,1987(21):1-17
[2]张兴芳,齐玉霞.区间值Fuzzy集的隶属原则及其应用[J].聊城师院学报,1998,11:12-15
[3]郭春香,郭耀煌.具有区间数的多目标格序决策方法研究[J].预测,2004,23:71-73
[4]刘俊娟.基于最大相对隶属度的区间数多指标评价在交通规划中的应用[J].现代交通技术,2007(4):59-72
[5]郭志林,陆凤玲.课堂教学质量的区间值模糊评判[J].南阳师范学院学报,2005(4):34-36

