单边直圆型柔性铰链位移精度的有限元分析*
沈剑英,李积武,赵 云
(嘉兴学院机电工程学院,浙江 嘉兴 314001)
0 引言
柔性铰链是一种新型的弹性导轨形式,具有无机械摩擦、无间隙、无热源、运动灵敏性高等优点,能够实现纳米分辨率定位,在精密机械、精密测量、生物医学工程、微电子技术和纳米技术等领域得到了广泛的应用,如STM、超精密工作台、精密微位移系统[1-3]。
各国学者纷纷开展柔性铰链的研究,Wei Xu等人[4]研究并比较了直圆型、椭圆型、导角型柔性铰链的精度性能,认为直圆型柔性铰链的精度性能最好。王纪武等人[5]采用有限元技术分析了在加载条件下不同几何参数对三种柔性铰功能方向和非功能方向精度性能的影响,给出特殊情况下柔性铰优化设计的准则。Nicolae[6]推导了抛物线、双曲线型柔性铰链的柔性、运动精度和应力特性的相关公式;陈贵敏[7]提出了深切口椭圆柔性铰链基于材料力学中的变截面梁的弯曲理论推导出了这类柔性铰链的转角、转动精度和最大应力的解析计算公式。
单边柔性铰链由于结构相对紧凑,在空间受限制的场合得到了应用,本文采用有限元法研究单边直圆柔性铰链的位移精度。
1 单边直圆柔性铰链
1.1 结构参数
单边直圆柔性铰链如图1所示,由于容易设计和制造,这种柔性铰链是最常见的类型之一,它的结构参数主要有切割半径R、最小厚度t、宽度b。
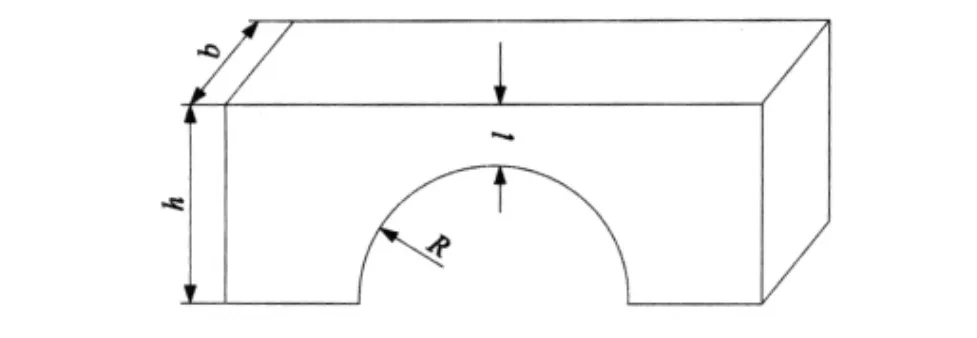
图1 柔性铰链的结构简图
1.2 精度性能
柔性铰链的中部较为薄弱,在力或力矩作用下可以产生较明显的弹性角变形,能在机械结构中起到铰链的作用。在理想情况下,柔性铰链绕其中心轴旋转,中心轴的位置应该保持固定不变。实际上,在力或力矩的作用下,柔性铰链的转动中心(图2中o点)也会产生偏移,从而影响了运动精度,偏移值越大,柔性铰链的精度性能就越低。
柔性铰链的变形是许多微小弯曲变形的累积结果,如图2所示,假设柔性铰链的左边为固定端,右边为自由端并受到力的作用。柔性铰链的变形量可用p点在y方向的位移值yp表示,转动中心o点的偏移值可用o点在y方向上的位移值yo来表示,根据力学知识得,yo<yp。

图2 柔性铰链的受力和变形图
实际应用中,需要较大的位移和高的位移精度,因此,在相同条件下,yp越大越好,而偏移值yo越小越好。为了衡量柔性铰链的精度性能,引入位移精度系数ε和偏移系数η二个系数。
位移精度系数ε由下式表示:

偏移系数η由下表示:

由式(1)、(2)知,位移精度系数ε和偏移系数是倒数关系,即

位移精度系数ε越大,说明柔性铰链的精度越高。偏移率(或偏移系数)η越大,说明柔性铰链的精度越低。由于偏移系数η小于1,偏移系数η用百分比表示,又可以称为偏移率。
2 有限元法分析
2.1 有限元建模和求解
为了更好地设计柔性铰链,需要深入研究基本参数R、t和b与位移精度系数ε、偏移率(或偏移系数)η之间的关系。要计算ε和η的值,先要知道yo、yp的值,为了得到ycyp的值,采用有限元软件ANSYS进行有限元仿真计算。
对于柔性铰链,随着基本参数R、t和b的变化,就有许多个模型,如果采用人机交互方式建立每一个分析模型,就会花费大量时间,降低分析效率,又容易出错。为了提高工作效率和节约时间,本文采用参数化建模方法,该方法利用ANSYS提供的APDL语言进行编程生成分析模型。在程序中把柔性铰链的结构参数R、t和b定义为变量,这样,改变一个参数值,ANSYS重新运行程序,就会生成对应的分析模型。
分析模型的基本参数如下:柔性铰链最小厚度t为1mm、切割圆弧半径 R为 3mm、铰链宽度 b为10mm。机构的材料选钢,它的弹性模量E为200Gpa。力矩M为12N·mm。采用8节点三维实体单元Solid45划分网格,柔性铰链的有限元模型和变形见图3和图4。
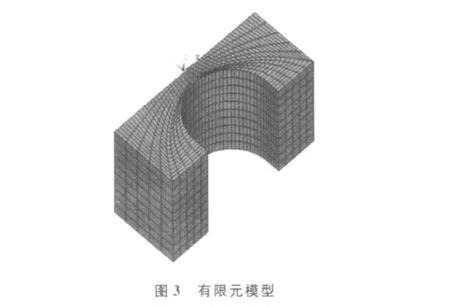

通过改变模型中参数R、t和b的值,每次就分别得到yc,yp的值,然后由式(1)和(2)计算出ε和η的值,最终结果见图5、图6。

图5 精度性能与结构参数之间的关系
2.2 结果和讨论
图5a显示随着铰链最小厚度t的增大,而位移精度系数ε减少;例如,在图中的中间曲线(此时切割半径R=3mm),当t从0.6mm增大到1.4mm时,位移精度系数相应地从11.78减少到7.05;换句话说,当t有0.8mm的增量时,位移精度系数减少了40.2%。从图5b可以看出,位移精度系数ε随着切割半径R的增大而增大;例如,当R从2mm增大到4mm时,位移精度系数相应地从6.94增大到10.10,即当R有2mm的增量时,位移精度系数增大了45.5%。
由于偏移率η和位移精度系数ε是倒数关系,图6a显示偏移率η随着铰链最小厚度t的增大而增大;例如,在图中的中间曲线(此时切割半径R=3mm),当t从0.6mm增大到1.4mm时,偏移率相应地从9.42%增大到15.57%。从图6b可以看出,偏移率η随着切割半径R的增大而减少;例如,当R从2mm增大到4mm时,偏移率相应地从14.41%减少到9.9%。

图6 偏移率与与结构参数之间的关系
从图5c、6c知,随着宽度b的增大或减小,位移精度系数和偏移率变化很小,在t越小,精度系数ε越高,偏移率η越小。
根据以上结果,设计单边直圆柔性铰链时,在满足柔性铰链强度的条件下,应该尽可能选取较小的最小厚度t和较大的切割半径R。
3 结束语
为了分析单边直圆柔性铰链的三个参数与柔性铰链位移精度系数ε和偏移率η之间的关系,利用ANSYS软件提供的参数化程序设计语言APDL编制程序,实现快速、方便地自动生成柔性铰链的参数化有限元分析模型。分析结果表明:随着最小厚度t的增大,位移精度系数ε减小,而偏移率η就增大;切割半径R增大,位移精度系数ε增大,而偏移率η减小,而宽度b的变化对位移精度系数ε和偏移率数η影响很小。本研究对于在结构紧凑的场合应用单边直圆柔性铰链具有重要的指导意义。
[1]J.Fu,R.D.Young,T.V.Vorburger.Long-range Scanning for Scanning Tunneling Microscopy[J].Rev.Sci.Instrum,1992,63(4):2200-2205.
[2]王生怀,陈育荣,王淑珍,等.三维精密位移系统的设计[J]. 光学精密工程,2010,18(1):175-182.
[3]王淑珍,王生怀,谢铁邦.大量程纳米级垂直扫描系统研究[J]. 中国机械工程,2010(4):387-390.
[4]Wei Xu,Tim King.Flexure hinges for piezoactuator displacement amplifiers:flexibility,accuracy,and stress considerations.Precision Engineering,1996,191(1):4-10.
[5]王纪武,陈恳,李嘉,等.典型柔性铰链精度性能的研究[J]. 清华大学学报(自然科学版),2001,41(11):49-52.
[6]N.Lobontiu,J.S.N.Paine,E.O’Malley,etc.Parabolic and hyperbolic flexure hinges:flexibility,motion precision and stress characterization based on compliance closed-form equations[J].Precision Engineering,2002,26(2):183-192.
[7]陈贵敏,韩琪.深切口椭圆柔性铰链[J].光学精密工程,2009,17(3):570-575.

