基于微切削的仿真模型研究*

苗 勇，李 迎

(南京理工大学机械工程学院，南京 210094)

0 引言

随着微型化构件的应用越来越多，微切削加工技术受到了广泛的关注。金属切削过程是热、力耦合作用的高度非线性问题。微切削除具有常规切削的一般特点以外，还有自身的特点。用传统的试验方法研究微切削十分困难，因为当加工精度达到微米、亚微米甚至纳米级时，必须借助于高分辨率的仪器和检测设备进行观察和分析。运用计算机技术进行理论分析和模拟，成为微观尺度切削加工研究的重要手段之一。

计算机模拟仿真方法是20世纪以来除理论模型和试验分析之外的第三种科学研究手段方法。用计算机仿真技术研究微切削可以成为试验研究的有效补充，目前用于微切削的仿真模型主要有有限元模型、分子动力学模型和多尺度模型三类。

1 有限元模型

有限元仿真方法已经广泛应用于宏观切削中，随着微切削研究的不断深入，有限元方法对微切削的研究不断发展。目前的研究主要集中在刀尖圆弧半径效应、应变梯度效应、材料特性、切屑成形和摩擦特性。

1.1 刀尖圆弧半径效应

Moriwaki等人［1］基于刚塑性有限元(RPFEM)理论建立了铜的微正交切削有限元模型。认为随着刀尖圆弧半径与未变形切削厚度的比值不断减小，切削比能增加;而当刀具圆弧半径与未变形切削厚度的比值不断增加时，应力分布区域有所扩展。Schulze等人［2］对微切削表面残余应力状态进行了研究。指出刀尖圆弧半径越大，包括塑性变形在内的等应力场的影响区域就越大，由此产生的拉伸残余应力的渗透层越深。

1.2 应变梯度效应

Dinesh等人［3］研究发现，除刀尖圆弧半径外应变梯度也是尺寸效应的重要方面。Liu等人［4］建立有限元应变梯度模型，用于预测微加工的尺寸效应。认为在考虑应变梯度影响时，应变区域有所减小但最大应变值更大。如图1所示，左侧不考虑应变梯度的影响，右侧考虑。

图1 应变等值图［4］

1.3 材料特性

当切削深度达到几十个纳米或几个纳米时，以工件材料为研究对象的微结构仅包含数个或数十个原子，所以加工现象在本质上是原子的、离散的，此时，被加工材料不再是宏观中各向同性的连续固体，而必须考虑到微观各向异性对加工的影响。

Chuzhoy等人［5］建立了球墨铸铁正交切削的有限元模型，在考虑到工件材料异构特性的情况下，对铁素体、珠光体等铸铁的不同形态进行了精确建模。一些学者运用这样的方法对最小切削厚度进行了研究，取得了较好的效果。

1.4 切屑成形

微切削中切屑分离是一个十分复杂的过程。Sathyan等人［6］通过建立牺牲层的方法来处理失效单元。自适应网格技术对减少单元扭曲具有重要作用，如任意拉格朗日欧拉(ALE)自适应网格和自适应网格重构技术。Mahnama等人［7］研究了切屑成形与机床震动的内在关系，运用有限元自适应网格技术结合机床系统的动态分析建立了切屑成形的有限元模型。此模型可用于预测实际加工过程的各种现象。模拟显示，随着切削宽度的不断增加，切削过程发生了稳态到临界稳态再到非稳态的转变。

1.5 摩擦特性

在微切削中，摩擦受到诸多因素的影响，如接触压力、温度、切削速度等。现在常用的摩擦模型是库伦摩擦模型。Pedro等人［8］将粘结和滑移摩擦相耦合，分别建立了刀具-切屑摩擦模型和刀具-工件摩擦模型，该模型不仅运用了任意拉格朗日欧拉(ALE)自适应网格技术还结合了热应力分析。作者认为当ALE有限元模型使用拉格朗日切屑边界条件时，预报力会随着极限剪切应力的增加而增大，极限剪切应力对摩擦模型有显著影响。

2 分子动力学模型

微纳米加工的物理实质是切断原子键的结合，实现原子或分子的去除。因此，用建立在连续介质力学基础上的有限元方法来解释纳米切削机理显然是不合适的。分子动力学仿真从分子和原子的角度出发，将研究对象抽象成一个粒子系统，通过模拟势函数及粒子动力学方程组反映粒子间的相互作用，运动规律和轨迹。Shimada等人［9］将分子动力学纳米加工的模拟过程与实验结果相比较，指出分子动力学适用于分析微纳尺度切削。目前研究的主要方向有刀具刃口半径、刀具前角、加工精度和刀具磨损。

2.1 刀具刃口半径

Ikaw等人［10］模拟了金刚石刀具单晶铜的纳米切削过程，研究了刀具刃口半径和切削最小厚度对切屑形成过程的影响，发现当非切屑厚度小于刀具刃口半径时，不会形成切屑。同时，他们还研究了刀具刃口半径与切削厚度的关系［11］，发现刀具刃口半径越小，切削厚度越小，最小切削厚度大约是刃口半径的1/20～1/10。Li等人［12］研究了金刚石刀具在脆性材料切削过程中刀具刃口半径的影响，结果发现刃口半径越小，粗糙度越小，但是当刃口半径小到一定程度时，由于刀具磨损粗糙度反而越来越大。

2.2 刀具前角

Luccal等人［13］以不同的刀具前角为参数，研究了锗的二维正交纳米切削过程中的轴向力和切削力。结果发现，随着切削深度的不断减小以及负前角的不断增大，轴向力与切削力的比值越来越大，并且随着负前角的越来越大，由表面裂纹导致的切削深度也越来越大。Kwon等人［14］指出在超精密加工中，当切削深度很小时，刀具负前角和工件的弹性回弹是尺寸效应的主要因素。作者在考虑了刀具几何形状和工件的弹性回弹的情况下建立了新的动力学模型。

2.3 加工精度

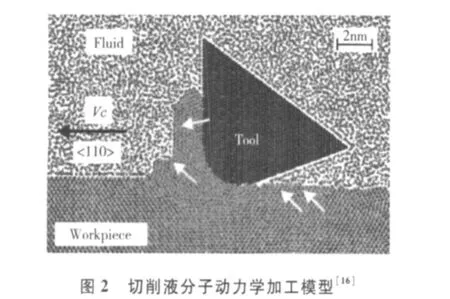
Shimsda等人［11］在对分子动力学深入研究的基础上，探讨了微切削中可能获得的极限精度问题，指出切削的最小厚度至少是lnm，最终工作表面粗糙度大约0.5nm，变形层深度可达5nm。Shoichi等人［15］对极限加工精度进行了进一步研究，指出在单晶铜的切削仿真条件下，极限表面粗糙度可以达到lnm或更小虽然在多晶铜的切削过程中，工件表面扭曲层依然存在，但最终的表面粗糙度与单晶铜相当。Rentsch等人［16］建立了切削液模型，研究了切削液对加工精度的影响。图2为有切削液时的加工模型，图3为真空下的加工模型。图3中绿线轮廓即为图2工件表面轮廓从图3白色箭头所指处可以看出，有切削液时的工件表面质量要优于真空。

2.4 刀具磨损

原子尺度的分子动力学模型比有限元模型更加精确，但计算时间成为限制分子动力学的最主要因素。Maekawa等人［17］为了节省计算时间提出了一种基于NoseHoover的有限区域分子动力学(ARMD)方法，通过降低碳原子间结合力模拟刀具磨损，指出刀具磨损的主要原因是工件和刀具原子的相互融合以及磨损的碳原子重新粘附于刀具。Cai等人［18］研究了单晶硅切削过程中金刚石刀具的磨损机理，结果显示随着加工区域温度的上升，金刚石刀具的表面材料发生了软化;由于加工区域较高的静水压力，工件材料发生了从单晶到非晶态的相变，这一过程产生了硬度是原硅材料数倍的原子组，这些更硬的原子在与刀具原子发生相对运动时，导致了刀具的磨损。Narulkar等人［19］建立了如图4分子动力学仿真模型。加工过程中刀具原子扩散到工件中导致了刀具磨损，这与试验相符。

3 多尺度模型

有限元仿真方法理论上局限于连续介质，对于微纳加工分子动力学仿真方法更适用且更精确，然而计算时间和仿真规模限制了分子动力学仿真方法的应用。针对这一情况，研究者提出了多尺度模拟方法，其基本思想是把分子动力学模型嵌入到连续介质模型中去，只对感兴趣的微小区域进行分子动力学方法计算，而对其它区域则采用连续介质力学方法进行计算，这样不仅减小了计算量、极大地扩展了计算尺度，而且计算精度也得以保持。目前具有代表性的研究是材料去除、应力应变和算法研究。

3.1 材料去除

Behrouz等人［20］研究了纳米尺度单晶铝材料去除工艺，认为位错的产生和扩展是切屑和工件表面成形的主要原因;当切削速度超过塑性波的传播速度时，法向力的平均值迅速增加;高速切削下的切削变形机理完全不同于低速切削下，如图5所示，图a显示了切削速度为200m/s时切屑结构为晶态，图b时切削速度为800m/s，此时切屑结构变为非晶态;从图中也可看出高速切削下的工件表面质量要优于低速下的。

图4 分子动力学的切削模型［19］

图5 不同切削速度下切屑形态和表面质量［2］

作者同时指出，高速切削(＞400m/s)状态下由于缺少位错，薄的原子模型更为适用，模拟显示此时分子动力学模型比多尺度模型更加高效;而低速切削(＜400m/s)时多尺度模型更适用。

Hongmin等人［21］研究了纳米尺度单晶铜不同切削速度的影响，指出当切削速度超过塑性波的传播速度时，单晶铜的材料变形机理将发生巨大改变;高速切削下，法向与切向力的平均值迅速增大。

3.2 应力应变

应力应变对于加工变形及表面质量等都有着重要影响。Inamura等人［22］将纳米切削与宏观切削相比较，基于原子模型到连续模型的转变方法计算纳米切削过程中应力应变的分布。指出宏观塑性理论无法解释纳米切削中应力应变的分布;工件沿着刀具前刀面的区域承受拉应变，而在主剪切带承受集中压应变和集中剪切应变;工具内部处于恒定高应力状态;微加工兼具纳米切削和宏观加工的特点，如微毛边成形可由分子动力学很好地描述，而晶粒或工件远场的应力应变分布可由有限元模型的宏观连续介质力学解释。

Inamura等人［23］研究了纳米切削过程中能量耗散和应力应变分布。发现与宏观切削相比，纳米切削过程中刀具下面工件塑性变形的能量耗散比宏观时多，而用于加工表面形成的能量与宏观时一样都很少;纳米切削过程中的应力应变分布与宏观情况一致，在主剪切带几乎没有集中的剪切应力。

3.3 算法研究

Tadmor等人［24］提出了 The quasicontinuum(QC)方法，为了构建一个完整的原子系统，引入有限单元概念，并将其直接耦合到分子计算中，这样减小了计算量，而且更接近实际。目前QC方法已经得到广泛的应用。孙西芝等人［25］基于QC方法模拟了单晶铝纳米切削过程，研究了刀具角度对切削过程的影响，发现在纳米加工中，刀具前角越大，工件内应力越小，切削力越小。

Lin等人［26］结合三维分子动力学和有限元形函数构建了molecular dynamics with finite element deformation model(MDFM)方法。如图6所示，随着刚体金刚石刀具逐渐进入工件，工件原子在刀具前方和切削方向两侧形成切屑，这与实际实验相符，从而证明了模型的合理性。

图6 第18000步时切削模拟

4 结束语

(1)有限元模型以连续介质力学为基础，这在很大程度上限制了有限元方法的应用范围，目前，大多研究者仅局限于从某一种因素考虑尺寸效应的影响;从二维模型到三维模型的扩展、切屑分离、摩擦特性还有待于深入研究。

(2)分子动力学从理论上更加适用于微纳加工，然而计算时间是限制分子动力学的最主要因素。用并行算法替代串行算法，可以使仿真规模有所提高;多尺度方法可以从本质上解决这一问题，因而备受关注。形式简单又能准确反映粒子间相互作用情况的模拟势函数和算法有待进一步改进;考虑各种缺陷、位错、晶界的多晶材料也是研究的方向。

(3)多尺度模型是当前关注的焦点，代表着未来的发展方向。目前的主要问题集中在研究材料过于理想;模拟势函数及算法有待完善;能够准确地描述原子模型和连续介质模型微观作用的耦合方法、多体势函数等还有待发展和完善。

［1］Moriwaki，T.，Sugimura，N.，Luan，S.，1993，Combined-Stress，Material Flow and Heat Analysis of Orthogonal Micromachining of Copper，CIRP Annals，42/1:75-78.

［2］.V.Schulze，H.Autenrieth，M.Deuchert，H.Weule.Investigation of surface near residual stress states after micro-cutting by finite element simulation.CIRP Annals-Manufacturing Technology 59(2010)117-120.

［3］.Dinesh，D.，Swaminathan，S.，Chandrasekar，S.，and Farris，T.N.，2001，“An Intrinsic Size-Effect in Machining Due to the Strain Gradient，”Proc.ASME Manufacturing Engineering Division ～MED-vol.12!，ASME International Mechanical Engineering Congress and Exposition，NY:197-204.

［4］.K.Liu and S.N.Melkote:Proc.Japan-USA Symposium on Flexible Automation(Denver，CO，July，2004).

［5］L.Chuzhoy，R.E.DeVor，S.G.Kapoor and D.J.Bammann:ASME Journal of Manufacturing Science and Engineering，2004，124:162.doi:10.1115/1.1455642.

［6］S.Subbiah and S.N.Melkote:Materials Science and Engineering Vol.474(A)(2008):283.

［7］.M.Mahnama，M.R.Movahhedy.Prediction of machining chatter based on FEM simulation of chip formation under dynamic conditions.International Journal of Machine Tools＆Manufacture 50(2010)611-620.

［8］.PedroJ.Arrazola，Tugrul ozel.Investigations on the effects of friction modeling in finite element simulation of machining.InternationalJournalofMechanicalSciences 52(2010)31-42.

［9］.Shimada S，Ikawa N，Ohmori G，et a1.Molecular dynamics analysis a8 compared with experimental result of micromachining［J］.Annals of the CIRP，1992，41(1):117-120.

［10］Ikawa，N.，Shimada，S.，and Tanaka，H.，1992，“Minimum Thickness of Cut in Micromachining，”Nanotechnology，3:6-9.

［11］Shimada S，Ikawa N，Tanaka H，el a1.Feasibility Study on Ultimate Accuracy in Microcutting Using Molecular Dynamics Simulation［J］.Annals ofthe CIRP 1993，42(1):91-94.

［12］Li D，Dong S，Liang YC，el a1.MDS study on the effect of cutting edge radius of diamond tools in nanometic cutting process for brittle materials.International Conference on Precision Engineering(ICPE)［C］.Yokoham a:Inasaki I，2001，294-298.

［13］D.A.Lucca，P.Chou，R.J.Hocken.Effect of Tool Edge Geometry on the Nanometric Cutting of Ge.CIRP Annals-Manufacturing Technology，1998，47(1):475-478.

［14］K.B.Kwon，D.W.Cho，S.J.Lee，C.N.Chu.A Fluid Dynamic Analysis Model of the Ultra-Precision Cutting Mechanism.CIRP Annals-Manufacturing Technology，1999，48(1):43-46.

［15］Shimada S，Ikawa N，Tanaka H，el a1.Structure of Micromachined Surface Simulated by Molecular Dynamics An alysis［J］l Annals of CIRP 1994，43(1):51-54.

［16］Rentsch R，Inasaki I.Effects of fluids on the surface generation in material removal processes—molecular dynamics simulation［J］.Annals of the CIRP，2006，55:4-8.

［17］Maekawa K，hoh A.Friction and tool wear in nano—scale machi·ning·a molecular dynamics approach［J］.Wear，1995，188:115-122.

［18］Cai M B，Li X P，Rahman M.Study of the mechanism of groove wear of the diamond tool in nanoscale ductile mode cutting of monocrystalline silicon［J］.J Manuf Sci Eng，2007，129:281-286.

［19］R.Narulkar，S.Bukkapatnam，L.M.Raff，R.Komanduri.Graphitization as a precursor to wear of diamond in machining pure iron:A molecular dynamics investigation.Computational Materials Science 45(2009):358-366.

［20］Behrouz Shiari，Ronald E.Miller，Dennis D.Klug.Multiscale simulation ofmaterialremovalprocesses atthe nanoscale.Journal of the Mechanics and Physics of Solids 55(2007):2384-2405.

［21］Hongmin PEN，Qingshun BAI，Yingchun LIANG，Mingjun CHEN.Multiscale simulation of nanometric cutting of single crystal copper——effect of different cutting speeds.Acta Metallurgica Sinica(English Letters)，2009，22(12):440-446.

［22］Inamura，T.Takezawa，N.，Kumai，Y.，and Sata，T.，1994，“On a Possible Mechanism of Shear Deformation in Nanoscale Cutting，”CIRP Ann.，43:47-50.

［23］T Inamura.N Takezawa.Y Kumaki Mechanics and energy dissipation in nanoscale cutting.CIRP Ann 1993(01).

［24］E.B.Tadmor，M.Ortiz，R.Phillips，Quasicontinuum analysis of defects in crystals，Phil.Mag.A 73(1996)1529-1563.

［25］孙西芝，陈时锦，程凯.基于多尺度仿真方法的单晶铝纳米切削过程研究［J］.南京理工大学学报(自然科学版)，2008，32(2):144-148.

［26］Zone-Ching Lin.Jen-Ching Huang，Yeau-Ren Jeng.3D nanoscale cutting model for nickel material.Journal of Materials Processing Technology 192-193(2007):27-36.