基于自相关过程的控制图的性能评价

张 黎，李晓莉

（郑州航空工业管理学院，郑州 450015）

0 引言

传统上零件制造过程在大部分情况下处于统计控制状态[1～3]，因此，在实际应用中，不管过程数据是否独立，往往不加检验直接应用于控制图，对过程进行监控。Alwan[4][5]对出现在教材、手册、软件、权威期刊等中所讨论的控制图进行了统计，发现有235个控制图的应用是错误的，其中违背了使用控制图的独立性假定条件的超过85%。Alwan把应用控制图的错误分为4种类型：（1）数据不独立，但过程可以描述为一个自相关的时间序列；（2）数据不独立，可以由时间序列加上一些确定的变量来描述；（3）数据不独立，但可以表示为确定的变量；（4）非正态；第一种类型几乎占了一半。因此，必须研究过程数据具有相关性对控制图的影响，以构建适用于相关性的监控方案。本文将以平均运行长度（ARL）为评价指标，在过程观测值为二阶自回归AR（2）模型下，讨论相关性对控制图性能的影响。

1 移动极差估计

AR（2）模型表示如下[6][7]：

其中过程观测值为{Z1，Z2，…，Zn}，φ1、φ2为介于（-1，1）之间的常数，μ为Zt的期望值（在不失一般性下假设μ=0），而αt为时间t时的纯噪声。在模型参数φ1、φ2不随时间变化的前提下，造成过程均值不稳定的一个可能原因就是μ的变化。所以本文分析的核心是：假设过程在控制状态下，αt为正态分布，Zt均值从开始为0偏移到δσ2时，以三种常用控制图监控过程并以ARL探讨其稳健性。

已知AR（2）自协方差为

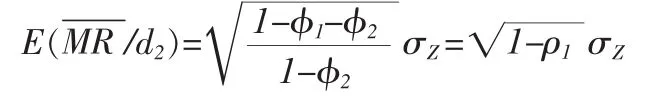
因此，当ρ1=0时，是过程标准差的无偏估计：否则，该估计值不是标准差的无偏估计，比例常数为

2 控制图的ARL

若Zt落在控制限之外，就判断过程存在特殊原因，过程失控。

以Zt建立单值休哈特控制图[2]，上下控制限为

同理，对于 Zt的 EWMA 统计量 Wt=λZt+（1-λ）Wt，建立EWMA控制图[8]，上下控制限为

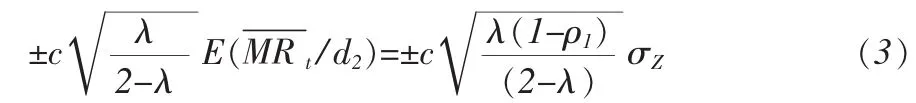
这里，λ=0.2，c=2.859。若Wt落在控制线之外，就判断过程失控。

CUSUM控制图的统计量为[9][10]

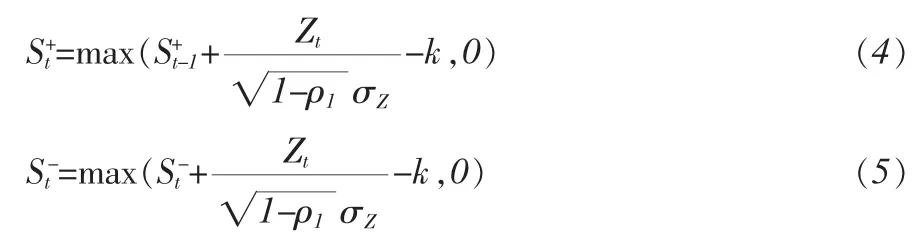
为了详细的分析相关性对控制图的影响，计算上述3种控制图的ARL。由于计算ARL的公式复杂，我们采用仿真的方法求出。对于不同参数的模型，在受控过程下（μ=0），重复仿真10000次，ARL0列于表1中；然后在失控状态下重复进行（μ=δσz），其 ARL1也列在表 1 中，表中未标出的表明 ARL的值超过3000。

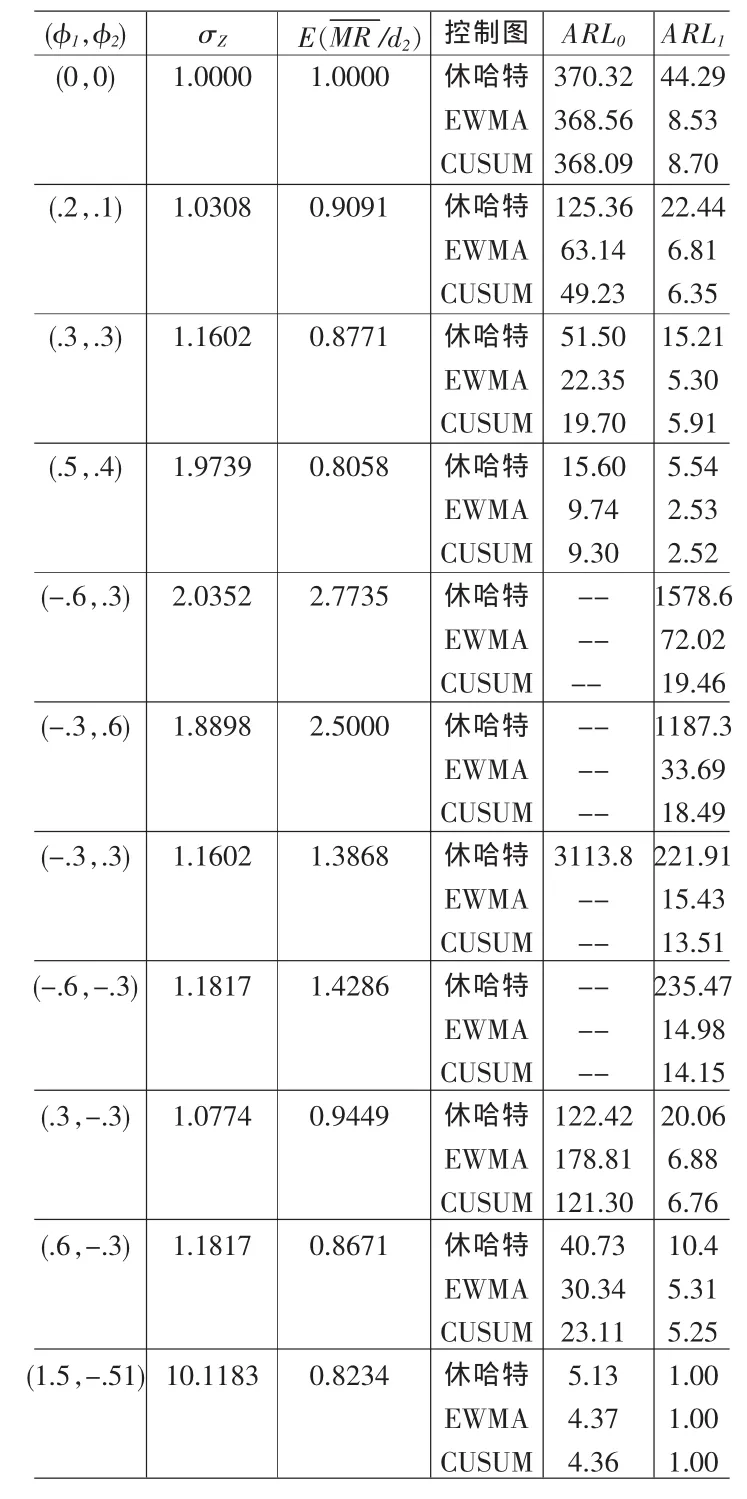
表1 AR（2）过程下控制图的性能

表中第1列是过程参数的不同组合；第2、3列为AR（2）过程的标准差和移动极差的期望值。从表中 看 到 ，φ1＞0的移动极差的期望值均小于标准差，这样，控制图的控制界限相对过紧，由此增加了假警报，降低了控制图的稳健性。而 φ1＜0时移动极差的期望值均大于标准差，由此控制界限过宽，容易漏发警报，从而降低了控制图的灵敏性。表中第5列、第6列的ARL进一步说明上述结果。

因此，在具有相关性的情况下，直接应用传统的控制图，一种情况使控制界限变宽，不能有效地及时发现特殊原因的存在；另一种情况使控制界限过紧，频繁的报警，导致对控制图的解释错误。其原因是移动极差估计是过程标准差的有偏估计，这样控制图不能正确地反映过程长期变化的情况。

3 仿真验证

为了更直观的考察相关对控制图的影响，并验证上述结论，现模拟两组自相关数据，以休哈特图和EWMA控制图为例，并与修正控制界限的休哈特图和EWMA图进行比较分析。在讨论之前，先来推导AR（2）过程下，EWMA统计量的方差，以建立修正界限的EWMA控制图。

AR（2）过程的方差为自协方差为 γk=Cov（Zt，Zt+k），EWMA 统计量为

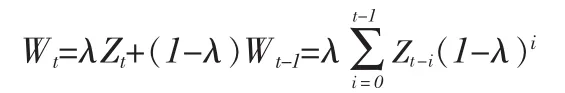
则

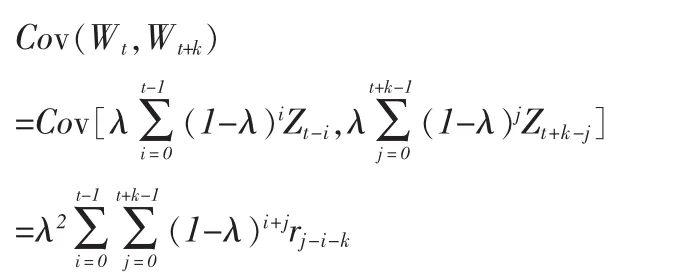
因为

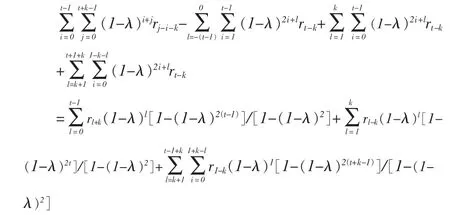
这样，

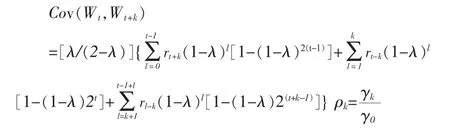
所以

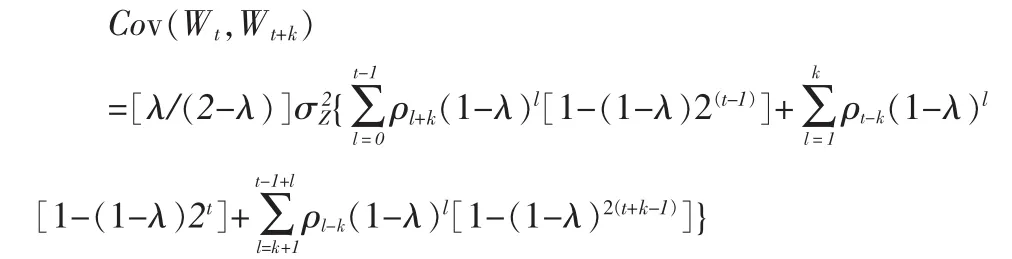
当t趋于无穷时，Wt收敛，这样，Wt是渐进平稳的。我们可以找到一个整数N，使

Cov（Wt，Wt+k）

因此，EWMA的近似方差为

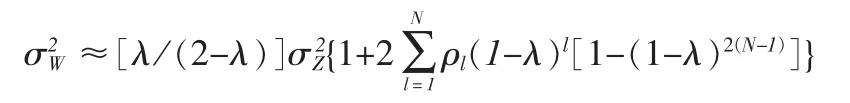
令 φ1=0.3，φ2=0.3，αt～N（0，1）。 模拟数据 100 个，前 80 个数据的过程均值μ=0；第81个数据后，假设过程受到特殊原因的影响，过程均值从零偏移到μ1=2σz=2.3204，图1表示Matlab软件模拟的100个数据序列。

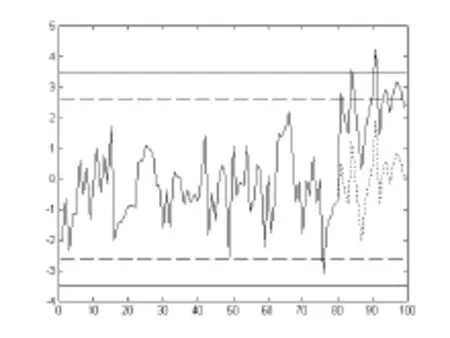
图1 休哈特控制图（φ1=0.3，φ2=0.3）

不考虑相关性，利用移动极差估计标准差，建立休哈特控制图，上下控制限分别为UCL=2.6313、LCL=-2.6313（图1虚线）。直观地看，图1中前80个值是平稳的，后20个值有向上的趋势，虚线所表示的20个值是没有偏移的情形。从图1中看到，第81点落在了控制限之外，这样在偏移发生之后就探测到均值偏移；但问题是图中前80个点有1点（第76点）也落在了控制线的外边，这是假警报。原因是没有考虑数据的自相关性，控制限过紧导致控制图发出假警报。由移动极差建立的休哈特控制图受控时的平均运行长度为51.50，相应于独立过程的假警报率是7.2。因此，不考虑自相关性，直接建立控制图监测过程是无效的。

如果考虑相关性，标准差σZ1.1602，建立修正控制限的休哈特控制图：±cσZ；并以受控时修正控制图的ARL近似于370.4，仿真确定参数 c=2.9734[5]，控制限 UCL=3.45，LCL=-3.45（图1实线）。注意到，前80个点全部在控制限内，均值偏移后的第85点落在了控制线之外。

图2 EWMA 控制图（φ1=0.3，φ2=0.3）

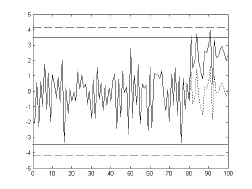
图3 休哈特控制图（φ1=0.3，φ2=0.3）

现在我们考虑使用同样的100个数据作EWMA图，如图2。不考虑相关性，同样使用移动极差估计标准差，λ=0.2，c=2.859，则 EWMA 的控制限为 UCL=0.83、LCL=-0.83（图 2虚线）。从图2中看到，前80个点中有4个点落在了控制限的外边。实际上，这个控制图在受控时的ARL=22.35，假警报率为16.5。因此，如此高的假警报使得EWMA图与休哈特图一样，不能正确的反映过程的波动信息。

同样，考虑到相关性，修正控制限的EWMA控制图：±σW。σW=0.4073，修正参数c=5.3507，这样EWMA的控制限为UCL=2.18、LCL=-2.18（图 2实线），在前 80个点没有报警，在均值偏移后的82点报警。

同理对于φ1=-0.3，φ2=0.3；休哈特控制图的控制界限，UCL=4.1604，LCL=-4.1604。 直观地看（图 3虚线），图 3中前80个值比图1更平稳，后20个值向上偏移，虚线图为没有偏移的图示。图中没有一次报警，并且前80个点的徘徊远离控制线。偏移后也没有报警。事实上，考虑自相关，过程标准差 σZ=1.1602，c=2.9734，控制限为 UCL=3.45，LCL=-3.45（图3实线），因此控制限相对过松，由此导致控制图不能发出警报，而考虑相关性的修正控制图在85点报警。

图4 EWMA 控制图（φ1=0.3，φ2=0.3）

同样对于φ1=-0.3，φ2=0.3不考虑相关性，建立EWMA控制图如图 4，UCL=1.32，LCL=-1.32（图 4 虚线），均值偏移后在84点发出警报，这是因为休哈特图偏移后ARL大于EWMA图。而考虑自相关，σW=0.2105，c=3.0409，上下控制限为 UCL=0.66，LCL=-0.58（图4实线），控制图仍然在第 82点发出了报警。

4 结论

传统的控制图监测并不包括数据自相关的情况，零件制造工业在过去使用控制图时假定过程数据是随机独立的，如果数据表现为正的相关性，控制图会频繁的发出警报。本文以自相关过程AR（2）为例，讨论了控制图直接监测自相关过程失效的原因，是由于移动极差估计是过程长期波动的有偏估计，仿真模拟试验的结果表明，当φ1＞0时控制图的控制界限相对过紧，降低了控制图的稳健性，而φ1＜0时控制界限过宽，降低了控制图的灵敏性。模拟数据比较了传统控制图和修正界限的控制图的监测的效果，验证了该结论。

[1]D.C.Montgomery.Introduction to Statistical Quality Control（4thEdition）[M].New York:John Wiley and Sons,2001.

[2]W.A.Shewhart．Statistical Msethod from the Viewpoint of Quality Control[M].Washington:Courier Dover Publications，1986.

[3]W.H.Woodall．Controversiesand Contradictions in Statistical Process Control[J].Journal of Quality Technology，2000， 32(4).

[4]L.C.Alwan.Statistical Process Analysis[M].New York:McGraw-Hill,2000.

[5]J.E.Wieringa.Statistical Process Control for Serially Correlated Data[EB/OL].http://www.ub.rug.nl/eldoc/dis/eco/j.e.wieringa/c1.pdf，2004-06-08．

[6]G.E.P.Box,G.M.Jenkins，G.C.Reinsel．Time Series Analysis,Forecasting and Control[M].London：Prentice-Hall,1994.

[7]杨位钦和顾岚．时间序列分析与动态数据建模[M]．北京：北京工业学院出版社，1986.

[8]J.N.Dyer,B.M.Adams，M.D.Conerly．The Reverse Moving Average Control Chart for Monitoring Autocorrelated Processes[J].Journal of Quality Technology，2003，35（2）.

[9]C.Lu，M.R Reynolds Jr．Cusum Charts For Monitoring An Autocorrelated Process[J].Journal of Quality Technology，2001,33（3）.

[10]O.O.Atienza,L.C.Tang，B.W.Ang.A CUSUM Scheme for Autocorrelated Observation s[J].Journal of Quality Technology，2002,34（2）.