宁波舟山近海三维潮汐潮流数值模拟
熊 伟 ,刘必劲 ,,孙昭晨 ,梁书秀 ,张亦飞
(1.大连理工大学海岸和近海工程国家重点实验室,大连 116023;2.国家海洋局杭州海洋工程勘测设计研究中心,杭州 310012)
宁波舟山近海三维潮汐潮流数值模拟
熊 伟1,刘必劲1,2,孙昭晨1,梁书秀1,张亦飞2
(1.大连理工大学海岸和近海工程国家重点实验室,大连 116023;2.国家海洋局杭州海洋工程勘测设计研究中心,杭州 310012)
利用FVCOM模型对宁波舟山近海的潮汐潮流进行了三维数值模拟,并对其水动力特性作了相应分析。FVCOM模型采用非结构化三角形网格,很好地解决了精确拟合宁波舟山群岛的复杂岸线的问题。基于计算区域内的海床性质,采用Koutitas公式对FVCOM模型的中海底摩阻系数的计算进行了改进。通过计算域内多个潮位站和海流站的实测资料验证表明,改进的摩阻系数计算公式是合理的,流场的计算结果与实测符合良好,可以用于三维污染物扩散和泥沙输移计算。
摩阻系数;潮汐;潮流;数值模拟;FVCOM模型
Biography:XIONG Wei(1988-),male,master student.
宁波舟山及其近海水域岛屿密布,漕滩相间,深水航道众多,地形极其复杂。由北往南的海湾主要有杭州湾、象山港和三门湾,这些都是强潮海湾且湾内有大面积的浅滩。宁波舟山群岛内的主要深水航道有金塘水道、册子水道、螺头水道、佛渡水道等。
国内学者对于杭州湾及浙江近海的潮流特性和数值模拟做了一定的研究。曹德明等[1-2]用有限差分法对杭州湾的潮汐、潮流进行了二维数值模拟;李身铎[3]采用垂向σ坐标下的三维数值模式模拟了杭州湾三维潮波运动;陈倩等[4]采用改进后的HAMSOM模式对浙江近海潮汐潮流进行了三维数值模拟;寿玮玮[5]采用ECOM模型对舟山群岛附近海域水动力场进行了三维数值模拟。但是大多数采用矩形网格和调和常数来模拟该区域内的流场,由于矩形网格不能很好地拟合这一区域的复杂岸线,加之采用调和常数进行潮流数值模拟,潮位和潮流的计算结果缺乏一定的精度,而且重要的是没有详细的讨论这一区域的海底摩阻系数的计算及其对水动力场的影响。采用基于有限体积法的三维FVCOM模型,利用宁波市海洋环境检测中心2009年对该区域进行的枯水期和丰水期水文调查实测资料,建立了宁波舟山及其近海的三维水动力模型,发现海底摩阻系数对这一区域的水动力场影响较大,并采用Koutitas公式计算这一区域的海底摩阻系数,经验证计算值与实测值符合良好。
1 FVCOM水动力模型
1.1 水动力控制方程组
FVCOM模型的全称是非结构网格的有限体积法海洋模式。该模型采用非结构化的三角形网格,能够精确的拟合复杂曲率的岸界;采用有限体积法,能够在整个计算区域内更好的保证了各物理量的守恒。该模型采用垂向静压假定,垂直方向采用σ坐标变换,使垂向沿水深的分层更趋合理。σ坐标下的连续性方程、动量方程和温盐方程如式(1)~式(5)

式(1)~式(3)分别是连续性方程、x方向的动量方程和y方向的动量方程,式(4)、式(5)分别是温度和盐度方程。其中u,v,ω分别是σ坐标系下的水平速度和垂向速度。σ取值从海底处-1到海表面处0。此模型采用新的MY-2.5湍流闭合模型求解垂向湍流黏滞系数和扩散系数。具体的湍动能扩散方程和详细描述见文献[6],具体的数值离散格式详见文献[7],这里不再一一赘述。
1.2 模型定解条件
1.2.1 自由表面条件
运动学边界条件

动力学边界条件

式中:τsx,τsy分别为风应力矢量在x和y方向上的分量。
温盐边界条件

式中:Qn(x,y,t)为表面静热通量;SW(x,y,0,t)为在海表面处短波辐射通量;cp为海水比热系数。
1.2.2 海底条件
运动学边界条件

动力学边界条件

式中:τbx,τby分别为底摩擦应力在x和y方向上的分量。
温盐边界条件

1.2.3 侧边界条件
侧边界可分为岸边界与开边界两种。
(1)岸边界:海岸线或沿岸建筑物即为不透水的岸边界,水质点沿岸线切向自由滑移,其边界条件为

式中:n为岸边界的法向量。
(2)开边界:FVCOM模型中有2种开边界条件,即采用调和常数或实时水位,本模型中采用实测潮位资料作为开边界。
2 模型的计算
2.1 计算区域与网格
由于杭州湾涨落潮流受到宁波舟山群岛的影响,并考虑已有实测潮位资料的站点位置,确定计算范围的开边界为北起芦潮港,往东至嵊山,然后转向西南,延伸至渔山列岛,最后与三门湾健跳相连;另外,将余姚和澉浦相连作为杭州湾内另一开边界。模型经纬度范围为120.902°E~122.800°E,28.885°N~30.855°N,计算范围如图1所示。网格数量为165 450,节点总数为86 659。网格步长最大3 500 m,最小为150 m,计算网格如图2所示。

图1 计算区域及验证站位图(Δ为潮位站,#为潮流站)Fig.1 Calculated range and distribution of stations

图2 计算网格图Fig.2 Gird of calculated range
2.2 模型计算参数的设置
本模型计算中垂向均匀分5层,时间步长取为1.0 s。考虑了研究区域内2009年枯水期(2月25日~3月11日)和丰水期(6月21日~7月5日)各15 d的潮位变化,开边界上的潮位根据主要潮位测站的实测潮位资料进行线性插值得到,所有测站的潮位高程基准面和水深基准面统一采用国家85高程。由于缺乏温度盐度的实测资料,本文中温度盐度不予计算。
2.2.1 海底摩阻系数的设置与讨论
在研究中发现这一区域的水动力场对海底摩阻系数甚为敏感,特在此做详细讨论。FVCOM模型中采用的海底摩阻系数计算表达式为

式中:k为卡门常数,一般取为0.4;zab为最底部水层的厚度;zo为海床糙率高度,其值的大小主要与床面泥沙的粒径、级配和床面几何形状有关。因此,Cd应该是与水深和底质类型有关的一个参数。由式(14)计算出的Cd≥0.002 5,而对于淤泥质海床,其zo一般很小,摩阻系数远小于0.002 5,在这种情况下,式(14)中取max值计算Cd并不合适。
在模拟过程中,针对杭州湾内1#测流站局部区域做了0.002 5和0.000 8两种摩阻系数下水动力的计算,将计算结果与实测流速大小进行了比较分析(图3)。由图3可以看出,摩阻系数取为0.002 5时计算流速与实测值比较明显偏小,摩阻系数取为0.000 8更为合适。同理,对象山县外海至象山港内做了0.002 5和0.001 0两种摩阻系数下水动力计算,将象山港内乌沙山站的计算潮位值与实测值比较(图4)。由图4可以看出,摩阻系数的选取对象山港这一区域的潮位过程曲线的影响也较大,当Cd=0.002 5时象山港内乌沙山站的计算潮位较实测值滞后现象较为明显,而Cd=0.001 0时,滞后现象并不存在。

图3 两种流速过程验证曲线的对比Fig.3 Comparison between two tidal current processes

图4 两种潮位过程验证曲线的对比Fig.4 Comparison between two tidal level processes
因此,对于淤泥质海岸,其海底摩阻系数一般很小且对水动力场的准确模拟有着很大影响,选取计算公式时应慎重。对多种摩阻计算公式的模拟结果进行比较,选取对数形式的摩阻系数计算式(Koutitas,1988)

式中:k为卡门常数,取为0.4。D为当地水深值;zo为海床糙率高度,其值的大小主要与床面泥沙的粒径和级配有关。在模拟过程中,根据流场计算值与实测值的比较,通过修改参数zo来改变摩阻系数的大小。本文的数学模型中,根据计算区域内表层底质采样的粒度分析数据显示,其中值粒径绝大多数都在0.01 mm左右,属于粘土质粉砂类,海床基本为淤泥质一类。经研究后,文中zo取为0.002 mm,计算的Cd值随水深地形在0.000 6~0.001 4范围内变化。
另外,海底的摩阻系数除反映海床粗糙度外,还包括了其他阻力因素对水流的综合影响,所以已不是原有意义的海床糙率,应当将其看成是一个综合阻力的影响因子。在水动力数值模拟计算中,由于计算范围的限制,对海岸工程建筑物会有不同程度的近似,此时可以根据需要在局部区域加大或减小摩阻系数来考虑流场阻力情况。
3 模型的验证
3.1 潮位计算验证
首先对研究区域的枯水期和丰水期各进行了15 d的水动力场计算。计算的初始条件为:当t=0时,u=v=w=ζ=0,其中 u,v分别为水平流速的x方向的分量和y方向的分量;w为垂向流速;ζ为未扰动海面上的潮位。整个计算域由静止开始计算,大约6 h后全场流态达到稳定。计算时按小时输出验证潮位站的潮位变化过程,用于对大小潮进行潮位验证。限于篇幅,文中只给出部分潮位测站丰水期大小潮的潮位验证过程曲线(图5)。由图5可知,丰水期时,宁波舟山及其近海海域的潮汐日不等现象在大潮期间表现的更为显著;枯水期(文中未给图)间,潮汐日不等现象在小潮期间表现的更为显著。其中高高潮与低高潮差值又以杭州湾和三门湾为最大,如洋山和乌沙山大潮期间这种差值达到近70~90 cm,桃花岛与北仑一带这种差值也在50 cm左右。从计算域内的潮差上来看,以杭州湾湾内的潮差最大,丰水期能达到8.0 m左右;其次是三门湾湾内,丰水期潮差达到6.0 m;以镇海北仑的潮差为最小。另外,南韭山站的潮位较虾峙门站的潮位提前20 min左右,这说明宁波舟山近海的潮汐由东南向西北方向传播。
3.2 潮流计算验证

图5 潮位过程验证曲线Fig.5 Validation of tidal level process
计算时按小时输出验证潮流站的流速流向变化过程,用于对大小潮进行流速流向验证。丰水期大潮期间的流速流向验证过程如图6所示,验证结果较为理想,只有2#站流速落潮流速稍大,2#测站位于涡旋附近,取与其相邻2个网格的计算速度,则没有这种落潮流速偏大的情况,因此可能是测流中测点位置移动的缘故。从图6可以看出,1#和2#潮流站的流速较大,峰值在1.2~2.0 m/s,其他的站点流速较小。从1#潮流站的流速流向可以看出,杭州湾涨潮流经过洋山以后以正西方向向湾内挺进;宁波舟山群岛内部海域水体往复流明显,其流向基本与岸线平行,由于岛屿的阻挡和地形约束,涨落潮流在途经这些水道时流速会陡然增大,最大流速在涨潮时偏向北岸,落潮时偏于南岸,这主要是由水道的开口方向和科氏力作用而引起的。
3.3 三维水动力分析
3.3.1 流场涨落过程及其特性分析
从计算的流场结果分析,外海潮波沿东南至西北方向向宁波舟山近岸海域传播。当潮波传过南韭山后,一部分直接进入象山港海域,另外一部分又分为两股,一股以较强流速穿越舟山群岛途经大衡山和大戢山向西进入杭州湾,一股穿过宁波舟山群岛内部海域(镇海北仑一带)的诸条水道继续北上进入杭州湾。计算全域内涨潮流场和落潮流场、穿山半岛附近涨潮流场和落潮流场如图7所示。
计算结果表明,杭州湾内的流向基本与其湾口走向一致,涨潮时平均流向为230°~300°,落潮时平均流向为60°~110°,涨落潮平均流向约为180°,近乎往复流性质。杭州湾北岸水域受涨潮流控制,水量为净输入;南岸水域受落潮流控制,水量为净输出。这一特点与杭州湾内高悬浮泥沙的成因即长江口向杭州湾内净输沙一致。在宁波舟山群岛内部的金塘水道和螺头水道内,涨落潮流形成明显的往复流,涨落流场结构基本一致,只是流动方向相反。从图7-c、图7-d中可以看出,涨潮时流速分布以北岸较大,落潮时流速分布以南岸较大。另外,在宁波舟山群岛内部众多岛屿附近,涨落潮时流场出现涡旋,与实测海流资料相符,这主要是由于群岛地形约束,过水断面窄,流速大而引起的。另外,潮波自外海传入象山港口门后,由于不断受地形影响及边界的反射作用,逐渐由前进潮波向驻波转变,其潮差由口门向湾内逐渐增大。高潮位沿程抬高,低潮位沿程降低。
3.3.2 流场垂向结构分析

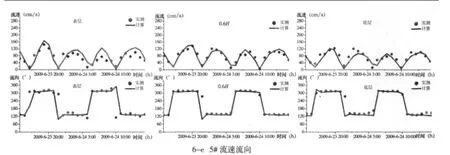
图6 流速流向验证曲线Fig.6 Validation of tidal current process

图7 三维水动力场计算结果Fig.7 Simulated results of 3D flow field
选取有代表性的三点即1#、2#和4#站的实测垂向流速结构进行分析(图8)。处在杭州湾的1#站分层流速随着水深的增大而逐渐减小,并且流速减小的幅度较大,表层比底层大近80 cm/s,可能由于杭州湾水深较浅(大部水深在10~15 m),流速受底部阻力因素影响所致;涨落时刻分层流向基本一致。2#站位于北仑附近的深水航道内,流速大小介于120~240 cm/s,其涨潮时刻流速大于落潮时刻,且涨潮时刻分层流速随水深的增大呈现先增大后减小的趋势,即最大流速并不是出现在流场表层;落潮时刻分层流速随水深的增大而减小,表层与底层流速差别较小;涨落时刻分层流向基本一致,与岸线平行。4#站位于象山港外的牛鼻山水道附近,此处是外海水进出象山港的主要通道,4#涨落时刻的分层流向基本一致;涨落潮时刻分层流速都随水深的增大而减小,但是涨潮时这种减小程度并不明显,底层比表层小20 cm/s左右;而落潮时的减小程度较大,底层比表层小80 cm/s左右;这可能受地形和过水面积的约束所致,涨潮时外海水进入水道,过水面积急剧减小;落潮时象山港内的水退入外海,过水面积急剧增大。由上可知,水深变化剧烈的深水航道内的垂向流速分布有别于一般开阔水域或地形平坦水域。

图8 测站实测垂向流速流向Fig.8 Measured tidal current at stations
4 小结
在准确拟合宁波舟山及其近海复杂岸线和改进底部摩阻系数计算公式的基础上,利用FVCOM模型对宁波舟山及其近海海域进行了三维水动力数值模拟。通过枯水期和丰水期实测水文数据和计算值的比较,验证了该模型的精确计算效果。这是首次将实测潮位资料和FVCOM模型应用于宁波舟山大范围海域内的三维潮汐潮流数值模拟,从计算效果看,该模型在研究近岸水动力学上有着独特的优越性。除模型的成功应用之外,本文得出以下结论:
(1)宁波舟山及其近海海域内海床基本为淤泥质,底部摩阻系数很小且其大小对水动力场影响较大,表现为流速明显偏小和局部潮位明显滞后,FVCOM中原摩阻计算公式并不适用于这一区域。文章经研究采用Koutitas公式计算摩阻系数,经模型验证该公式是合理的。
(2)杭州湾内的流向基本与其湾口走向一致,涨落潮平均流向夹角约为180°,近乎往复流性质。宁波舟山海域内潮汐日不等现象显著,在枯水期间以小潮表现更为显著,丰水期间以大潮表现更为显著,日不等现象由外海至近岸逐渐增强。
(3)宁波舟山群岛内部海域(镇海北仑一带)涨落潮流形成明显的往复流,涨落潮流场基本结构一致。
(4)受地形的影响及边界的反射作用,象山港内的潮差由口门向湾内逐渐增大,高潮位沿程抬高,低潮位沿程降低。
(5)对于三维流场垂向分层流速结构,水深变化大的深水航道内,其流速分布随水深先增大后减小,这有别于一般开阔水域或水深变化小的水域。
本次数值模拟的精度达到了要求,取得了好的模拟效果,但是对宁波舟山及其近海这一大范围区域来说,地形复杂,深水航道处较多而且水深变化剧烈,其海底底部糙率系数不仅仅只是和水深、海底糙率有关,因此这一区域内海底摩阻系数的计算和选取仍然是一个有待于进一步研究的问题。
致谢:本文采用的实测潮位潮流资料均来源于宁波市海洋环境监测中心2009年的海洋水文调查,特致感谢。
[1]曹德明,方国洪.杭州湾潮汐潮流的数值计算[J].海洋和湖沼,1986,17(2):93-101.
CAO D M,FANG G H.A Numerical computation of the tides and tidal currents in Hangzhou bay[J].Oceanalogia et limnologia sinica,1986,17(2):93-101.
[2]曹德明,方国洪.杭州湾和钱塘江潮波的联合数值模型[J].海洋学报,1988,10(5):521-530.
[3]李身铎,顾思美.杭州湾潮波三维数值模拟[J].海洋与湖沼,1993,24(1):7-15.
LI S D,GU S M.3D Numerical simulation of tidal waves in Hangzhou bay[J].Oceanalogia et limnologia sinica,1993,24(1):7-15.
[4]陈倩,黄大吉,章本照.浙江近海潮汐潮流的数值模拟[J].海洋学报,2003,25(5):9-19.
CHEN Q,HUANG D J,ZHANG B Z.Numerical simulation of tide and tidal currents in the seas adjacent to Zhejiang[J].Acta Oceanologica Sinica,2003,25(5):9-19.
[5]寿玮玮,吴建政,胡日军,等.舟山群岛附近海域三维水动力数值模拟[J].海洋地质动态,2009,25(11):1-9.
[6]吴伦宇.基于FVCOM的浪、流、泥沙模型耦合及应用[D].青岛:中国海洋大学,2009.
[7]朱建荣.海洋数值计算方法和数值模拟[M].北京:海洋出版社,2003.
[8]宋志尧.平面潮流数值模拟中底床摩阻系数的修正[J].水动力学研究与进展,2001,A16(1):56-61.
SONG Z Y.A correction of formula for bed resistance coefficient in numerical simulation of plane tidal current[J].Journal of hydrodynamics,2001,A16(1):56-61.
[9]Koutitas C G.Mathematical models in coastal engineering[M].London:Pentech Press,1988.
3D numerical simulation of tide and tidal currents in sea adjacent to Ningbo and Zhoushan
XIONG Wei1,LIU Bi-jin1,2,SUN Zhao-chen1,LIANG Shu-xiu1,ZHANG Yi-fei2
(1.State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian116023,China;2.Hangzhou Investigation Design Institute of Ocean Engineering,State Oceanic Administration,Hangzhou310012,China)
By means of FVCOM model,the tide and tidal currents in the seas adjacent to Ningbo and Zhoushan were simulated.Furthermore,the dynamic characteristics of tide were analyzed.The grid system of FVCOM model was unstructured triangle mesh,which solved the accurate fitting of complex of Ningbo and Zhoushan shoreline.Based on the property of seabed in the calculation zone,Koutitas formula was used to instead of the original calculation method of drag coefficient in FVCOM.Comparing the computed values with those tidal observatories,the improved formula proved to be reasonable and the two values are in good agreement.The computed model can be used for 3D pollutant concentration and sediment transport calculation.
drag coefficient;tide;tidal currents;numerical simulation;FVCOM model
P 731.23;O 242.1
A
1005-8443(2011)06-0399-09
2011-06-20;
2011-07-13
宁波市海洋泥沙水动力环境调查与建设用海区域评价项目(1102-082028);水沙科学及水灾害防治湖南省重点实验室开放课题基金资助项目(2011SS01)
熊伟(1988-),男,湖北省荆州市人,硕士研究生,主要从事海岸水动力学及泥沙运动研究。

