水流作用下地形不稳定性计算模型

王明明，邹志利

（大连理工大学海岸和近海工程国家重点实验室，大连 116024）

水流作用下地形不稳定性计算模型

王明明，邹志利

（大连理工大学海岸和近海工程国家重点实验室，大连 116024）

河流中水流和水底泥沙之间的相互作用会产生各种复杂的地形形态，交替型沙坝是其中的一种地貌特征，研究表明这一地貌的形成机理是水底地形的不稳定性。给出了这一不稳定性所导致的交替型沙坝的数值模拟方法和相应结果。水流方程采用了交替方向隐式算法求解，水底变形方程采用了比传统方法更加稳定的欧拉加权基本无振荡迎风格式求解，从而建立了水流与水底地形变化耦合计算模型。运用该模型研究了初始地形扰动产生的交替沙坝在长直河道中的演变。

地形演变；非线性；WENO；不稳定性

Biography：WANG Ming-ming（1986-），male，master student.

近岸区域和河流中地形演变依赖于水流、波浪、泥沙之间复杂的相互作用，水流作用下地形的不稳定性是这一复杂相互作用的突出表现形式。这一不稳定性导致水底地形即使是在初始时刻是均匀平直的水流作用下也会产生沿空间和时间变化的地貌特征，交替型沙坝就是这种复杂地貌特征的常见典型例子。在求解这种地形和水动力相互作用所引起的水底不稳定性问题时，如何求解地形演变方程是地形变化数值模拟中的一个难题，因为该方程是非线性的，会导致间断解的出现。以往多采用Lax-Wendroff格式［1］或者其改进后的格式，这些格式在地形峰值后面会产生数值振荡，从而不能够模拟地形的长时间演变过程。Hundson［2］对比了Lax-Friedrichs格式、Lax-Wendroff格式和MacCormack格式，提出更加稳定的Roe格式，但是很难应用于二维模型。加权基本无振荡（Weighted Essentially Non-Oscillatory）格式是1994年由Liu和Osher等［3］在ENO（Essentially Non-Oscillatory）构造思想的基础上提出的。ENO［4］格式具有在间断区分辨率高等优点。为了进一步提高该格式的计算精度，WENO格式引入了变化的加权因子，使计算结果更加稳定［5］。文章研究了地形和水动力相互作用所引起的水底地形不稳定性中WENO格式的应用问题。对水流方程仍然采用了常用的ADI方法［6］，但对地形演变方程采用了Euler-WENO方法，在此基础上建立了水流与水底地形变化耦合计算模型，并与传统的FTCS离散格式建立的模型的计算结果进行对比。应用该模型对交替沙坝地形的二维长直河道的形成进行了数值模拟，给出了这种地形形成的不稳定性机理的数值模拟结果。

图1 坐标系统Fig.1 Coordinate system

1 水流和水底地形的耦合数学模型

考虑一有限宽度的长直河道，取x轴和y轴分别沿河道的长度方向和宽度方向。水底沿x方向有一个微小的倾角i0，初始水流沿整个河道是均匀的。水流和地形变化满足以下基本方程。

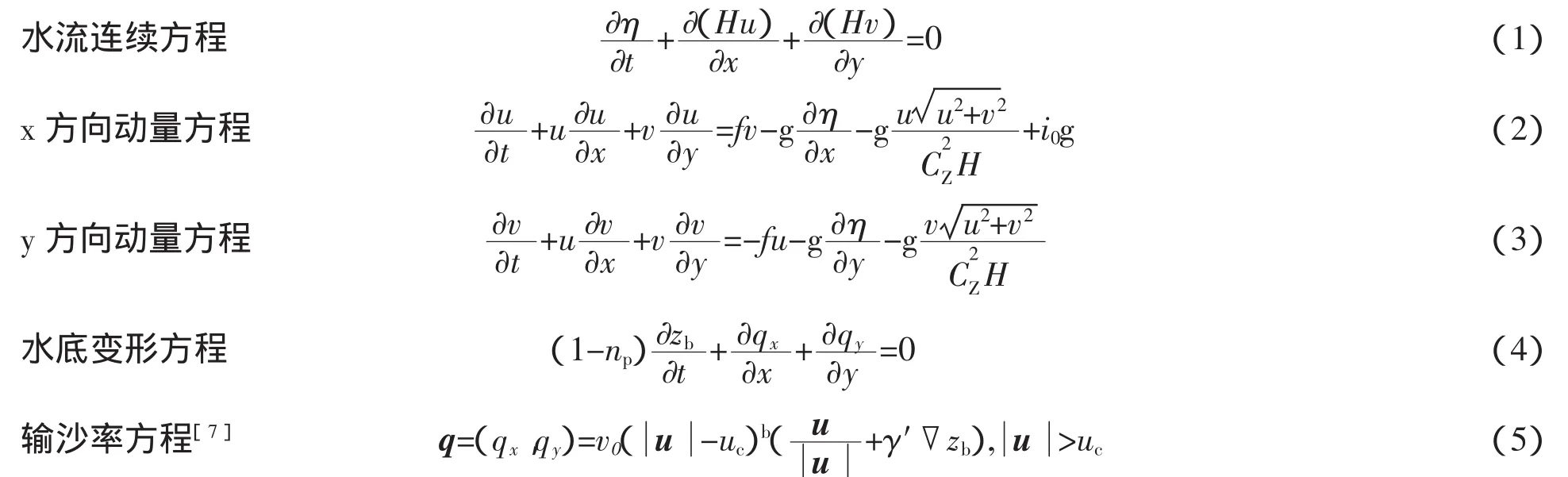
式中：u=（u，v）为水流流速矢量；η为水面升高，即自由水面与静水面之间的距离；H为总水深，H=η+h*-zb，h*为静水水深，zb为床面高程；Lx，Ly分别为河道的长度和宽度；f为科氏力系数（f=2ωsinφ，ω为地球自转速度，φ为河流所处的当地纬度）；Cz=H1/6/nr为谢才系数，nr为水底糙率；g为重力加速度；vo是与泥沙粒径相关的参数，一般取经验值。若将空隙率np考虑在内，可以用v来代替vo；q=（qx，qy）为推移质体积输沙率；b取值范围通常在2～7；uc为推移质的起动流速；γ′▽zb为坡度项，表示泥沙顺坡向下滑动的趋势，坡度项能使计算得到的沙丘形状更符合实际，γ′通常取1。这里泥沙输移只考虑推移质输沙。

文中对水动力方程（1）～（3）采用了ADI（交替方向隐式）法，网格划分如图2所示。计算时将每个时间步（t→t+Δt）的计算分成两步：在t→t+Δt/2，连续方程和x方向的动量方程采用半隐式格式离散，而y方向的动量方程采用显式格式离散；在t+Δt/2→t+Δt，连续方程和y方向的动量方程采用半隐式格式离散，而x方向的动量方程采用显式格式离散。在每个时间分步，可形成以η为变量的三对角方程组，从而可采用追赶法快速求解。下面仅给出前半步t→t+Δt/2的离散过程，后半步的离散过程与此类似。

vn+1/2的显示求解：

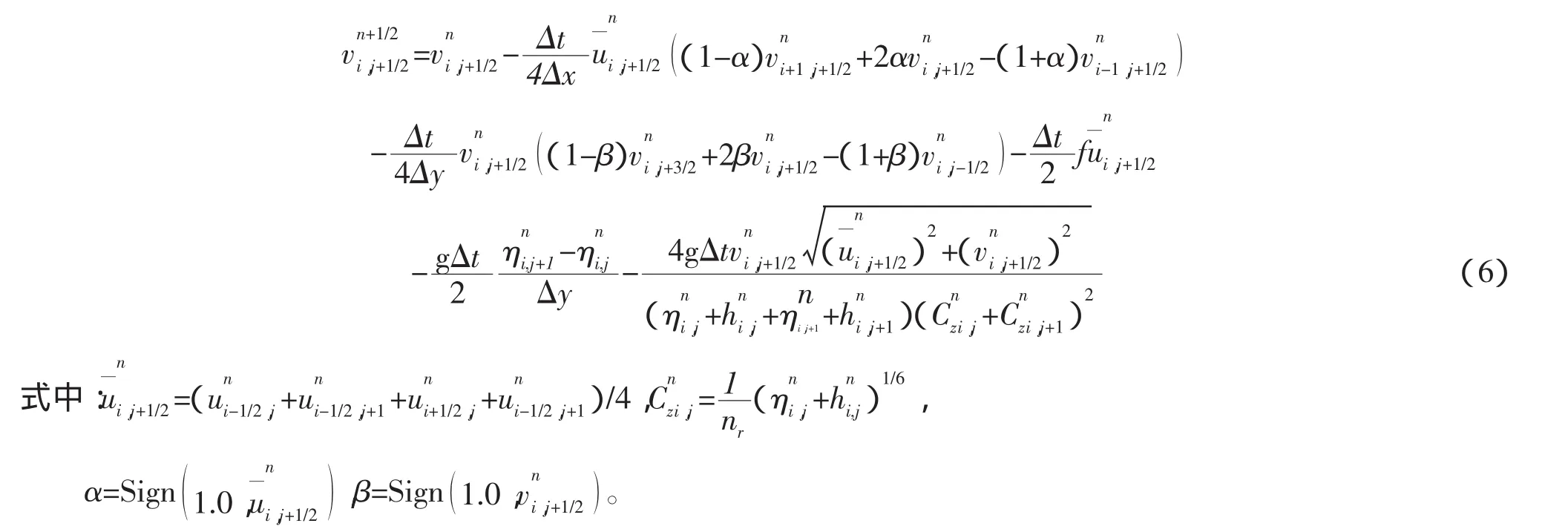
图2 交错网格布置图Fig.2 Disposition of variables in staggered grid

un+1/2的半隐式求解：

x方向的动量方程采用半隐式离散，其离散格式为

对水底变形方程（4），最简单的离散格式为FTCS（forward in time，central in space），即时间上向前差分，空间上采用中心差分。具体离散格式为

FTCS格式虽然形式简单易懂，但对于求解水底变形方程非常不稳定（第2节和第4节中详细给出了FTCS格式在一维和二维地形演变计算中出现的不稳定情况）。为了克服该格式的不足，本文除了采用该格式外，还采用如第1节所述的加权基本无振荡WENO格式。该格式具有在间断区分辨率高且具有五阶精度［8］等特点，可以为建立一个稳定精确的水流与水底地形变化耦合计算模型提供基础。下面以一维情况为例，介绍WENO方法应用的具体步骤［9］。

将输沙率q在x正方向和负方向分解成与地形传播速度相关的两部分

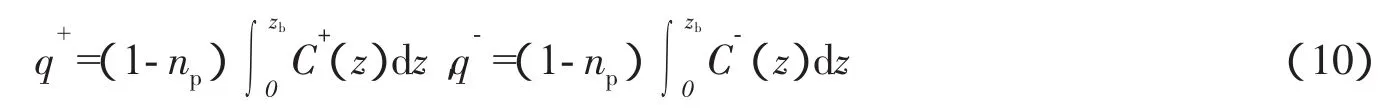
二维水底变形方程的Euler-WENO离散格式与以上处理完全类似，即将x方向和y方向的输沙率（qx，qy）都按上面计算q的方法计算（式（15）中各量也同样适用）。所对应的差分方程为

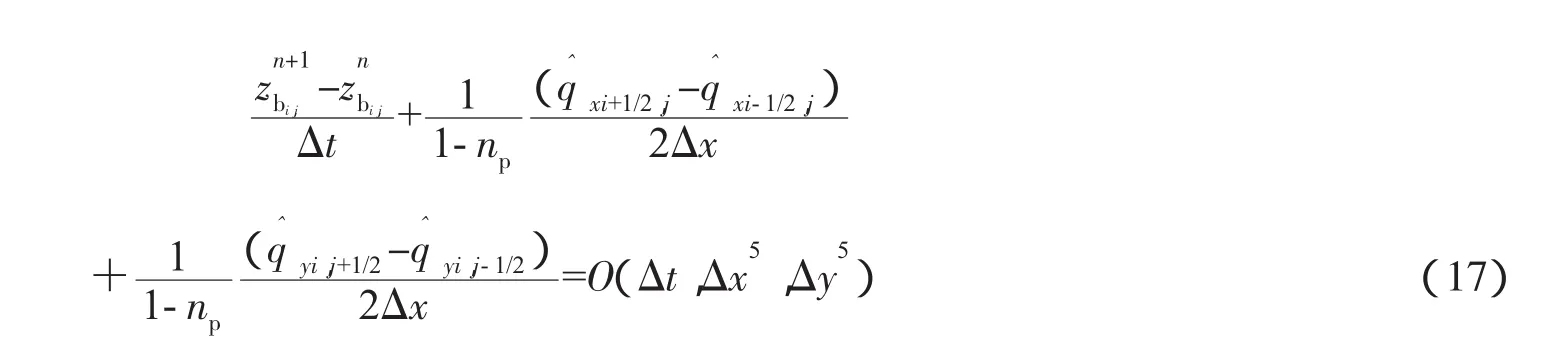
在第2节和第4节中将具体讨论Euler-WENO格式在计算地形演变时的精度和稳定性。

2 模型验证

2.1 水动力模型验证

取一平底河道，长1 320 m，宽220 m，水深5 m，坡度i0=6.11×10-5，将坐标系x取在水底平面上，z轴垂直水底向上。流速为1.0 m/s稳定水流。在渠道两端处施加出流边界条件。由于沿y方向地形没有变化，不考虑科氏力影响，因此由x方向动量方程可得

将 u=1.0 m/s，H=5.0 m，Cz=H1/6/nr代入式（18），解得糙度 nr=0.022 856。

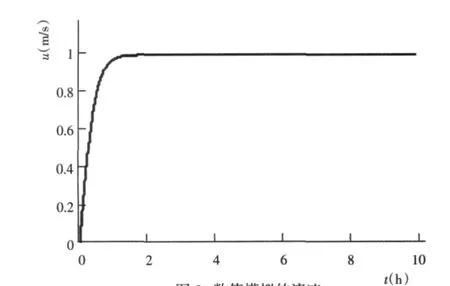
图3 数值模拟的流速Fig.3 Simulation of velocity

将nr=0.022 856代入数值模型，模拟结果如图3所示。流场在2 h左右达到稳定，得到的流速为0.999996m/s，水动力数值模拟结果与解析解吻合良好。

2.2 地形演变模型验证

Hudson给出了在长1 000 m、水深10 m矩形水槽中高1.0 m的沙丘在单向水流作用下的演变解析解，本节将分别采用FTCS方法和Euler-WENO方法模拟该问题并与Hudson得到的解析解进行比较。计算时所采用的地形、输沙率公式和其他参数同Hudson的一致。

初始地形为

地形方程为方程（4）的一维形式，输沙率公式为 q=aub，a=0.001 s2/m，b=3.0，np=0.4。

图4和图5分别给出了4个时刻的FTCS方法和Euler-WENO方法计算结果与Hudson的解析解的对比。图4和图5中从左到右依次为t=0 s（初始地形）、t=93 035 s、t=186 070 s、t=238 079 s时的地形。

图4 FTCS格式计算结果与解析解的对比Fig.4 Comparison between FTCS results and analytical solutions

图5 Euler格式计算结果与解析解的对比Fig.5 Comparison between Euler-WENO results and analytical solutions

由图4可知，FTCS格式在t=93 035 s和t=186 070 s2个时刻的计算结果与解析解吻合；但是随着计算时间增长，在t=238 079 s时，沙丘顶部出现数值振荡，与解析解不完全吻合；由图5可知，Euler-WENO格式的计算结果在3个时刻都能与解析解吻合，并且未出现类似FTCS格式的不稳定振荡。这些结果表明，Euler-WENO格式在求解水底变形方程时计算精度较高，且长时间计算过程中稳定性优于FTCS格式，因此适合用来模拟计算水底演变。

3 河流水底地形不稳定性

目前研究表明，虽然河流中水流是平直的，但水底地形不能保持平面形态，受到微小地形变化的扰动后，产生沙纹和较大尺寸的交替型沙坝等复杂地形形态，这一水底变形特征即为河流地形的不稳定性。Colombini［10］对长直渠道中的交替沙坝的演变进行了线性稳定性分析，表明非线性作用能够抑制地形波动峰值的无限增长，从而使波动达到一个稳定的峰值。Schielen［11］在Colombini的基础上得到了一个用于描述不稳定交替沙坝群包络振幅非线性演变的Ginzburg-Landau方程，结果表明，周期性的沙坝样式会变得不稳定，并表现出准周期性的变化特征。本节给出有关不稳定性线性化理论分析结果，为下一节将通过数值模拟给出非线性的地形不稳定性数值模拟结果提供基础。

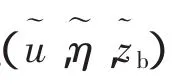
将（21）、（22）、（23）三式代入模型方程（1）～（5），假设扰动为小量，将控制方程线性化，得到关于扰动量的控制方程。假定扰动量的解的形式为

式中：ω=ωr+iωi，ωr为地形的波动频率，ωi为增长率，ωi＞0 表示地形扰动随时间增长，地形是不稳定的；k 为扰动波数。将式（24）代入控制扰动量的控制方程，可得到ω和k的关系，其数值结果如图6所示（无因次结果）。

图6 ω和k的关系曲线Fig.6 Relation curves ofωand k

图 6 中无因次波数 k′=2π/λ′，λ′=λx/Ly为无因次的地形扰动波长。由图 6可见，k′在一定范围内（0.19～3.32），有ωi＞0，即地形在这些波数情况下会变得不稳定；在k=1.05时，ωi的值达到最大。下一节将针对这一波数情况对正体扰动的演化进行数值模拟，以了解地形扰动的演化过程和将正体上节所介绍的数值方法应用于数值模拟这一演化过程。

4 非线性水底地形不稳定数值模拟研究

由第2节知，水底变形方程（5）的非线性特征（方程中输沙率对地形变化zb存在着非线性依赖关系）要求其求解的计算格式具有较高的分辨率，传统的计算格式（如FTCS方法），虽方法简单，但却存在数值振荡（图5），所以不能用于地形演变的计算研究，而Euler-WENO方法可以克服这些不足。下面将针对二维水底地形演变来继续探讨这一问题。计算针对上节给出的最大不稳定波数k=1.05的地形演变情况，将分别采用FTCS格式和Euler-WENO格式来模拟对应的二维水底地形不稳定性演变。

图7 初始扰动地形Fig.7 Initially perturbed bed

如同上面第1节一样，考虑一个有限长度的具有微小倾角的长直渠道，其初始时刻水底为平直的。将坐标系x和y轴取在水底平面上，具体坐标系统如图1所示。在初始地形上加入以下地形变化的扰动

该扰动在x方向和y方向都是按余弦函数变化的，zb0为扰动的幅值，kx和ky分别为x方向和y方向上的地形扰动的波数：kx=2π/λx，ky=2π/λy，λx和 λy分别为扰动波长。记 Lx和 Ly分别为计算域所包含的渠道的长和宽。计算中取Lx=λx，Ly=0.5λy。由上一节理论分析知，最大不稳定地形波数为k′=1.05，即

该式给出的地形扰动x方向波长为λx=2πLy/k′，即最大不稳定扰动的波长是依赖于渠道的宽度Ly。文中计算取Ly=220 m，所以可得扰动波长

因此计算时近似取λx=1 320 m，对应的计算域的长度Lx=λx=1 320 m。其他参数取值为：静水水深h*=5.0 m，扰动幅值 zb0=1.0 m，输沙率公式中系数 v=0.1，b=6，γ′=1，uc=0，糙率 nr=0.022 856，坡度 i0=6.11×10-5。具有这些参数的初始地形如图7所示。

地形边界采取周期性边界条件 qy|y=0=0，qy|y=Ly=0，qx|x=0=qx|x=Lx，zb|x=0=zb|x=Lx。

图8 FTCS格式地形演变三维图Fig.8 Bed evolution of FTCS scheme in 3D

图9 Euler-WENO格式地形演变三维图Fig.9 Bed evolution of Euler-WENO scheme in 3D

图8给出了FTCS格式在不同时刻t=2 h和5 h的计算结果。由图8可知，FTCS格式计算进行2 h，左右边界处的地形开始出现轻微振荡；随着计算时间的继续增加，边界处地形的振荡幅值增加，并且振荡范围向域内扩展；整个计算过程只能维持5 h左右，这时地形振荡明显，幅值较大，造成计算发散。图9中给出了对应的Euler-WENO方法的计算结果，与图8中FTCS方法的结果不同，地形整体光滑，未出现类似图8中的数值振荡。为了进一步显示该方法的计算稳定性，图10给出了第14 h和40 h地形结果，仍未出现振荡，表明该方法能够适应长时间地形演变的模拟计算。由图10可见，地形在x方向上顺水流向前移动，波动幅值随计算时间逐渐增长，地形波动不再呈初始时刻的余弦曲线状，而是向锯齿形剖面形状演化。从第14 h的三维地形图可以看出，峰值两侧地形逐渐不对称，地形峰值上游呈缓坡状，下游成陡坡状。

图11给出了8个时刻地形的等高线图。图11中结果显示，3 h过后，地形开始发生比较明显的变化。地形向前移动的同时，沿y方向上也开始有轻微变化，等高线轮廓不再保持左右对称，随着计算时间增加，不对称性更加明显；由图11中水流速度矢量可见，流场也随着地形移动出现轻微的摆动。图12给出了靠近边界点（x，y）=（660 m，210 m）处的地形和流速的随时间的变化历程。由图12可知，地形波动的最大幅值由最初的1.0 m在30 h增大到2.0 m，之后保持为常数，地形演变在30 h左右达到一种稳定状态。图12中流速在30 h以后呈周期性变化，波动周期为14.5 h。

图10 Euler-WENO格式地形演变三维图Fig.10 Bed evolution of Euler-WENO scheme in 3D

图11 地形演变等高线图Fig.11 Contour ofbed evolution

综合以上结果可知，采用Euler-WENO格式的计算地形演变，在精度和稳定性方面都优于传统的FTCS方法，且能够用于长时间的地形演变研究。

图12 点（660 m，210 m）处u，v和zb的时间历程Fig.12 Time series of u ，v and zbat（660 m，210 m）

5 结论

文章采用交替方向隐式格式（ADI）求解水动力方程，结合采用具有五阶精度的Euler-WENO格式求解的水底变形方程，建立了水流与水底地形变化耦合计算模型。通过对比FTCS格式和Euler-WENO格式求解一维和二维地形演变的计算结果，得知Euler-WENO格式在精度和稳定性上都明显优于传统FTCS格式，能够用于模拟长时间地形演变过程。

同时应用该模型研究了河流水底地形的不稳定性，模拟结果表明交替沙坝地形在单向水流作用下，地形变得不稳定，地形变化是三维的，沿纵向和横向都呈周期性变化，并且方程的非线性特征导致波动峰值是前后不对称的，呈锯齿形变形。波动在一定时刻（本文计算为30 h）达到一个稳定峰值；对应的水流变化也呈现出周期性波动。水流和地形的变化是相互耦合的。

［1］Hakeem K J，Julio A Z.Controlling spatial oscillations in bed level update schemes［J］.Coastal Engineering，2002，46：109-126.

［2］Justin H，Jesper D，Nick D，et al.Numerical approaches for 1D morphodynamic modelling［J］.Coastal Engineering，2005，52：691-707.

［3］LIU X D，Osher S，CHAN T.Weighted essentially non-oscillatory schemes［J］.Comput.Phys.，1994，115：200-212.

［4］Harten A.High resolution schemes for hyperbolic conservation laws［J］.Comput.Phys.，1983，49：357-393.

［5］赵海洋，刘伟，万国新.加权基本无振荡格式研究进展［J］.力学季刊，2005，26（1）：87-95.

ZHAO H Y，LIU W，WAN G X.Research on weighted essentially non-oscillatory schemes［J］.Chinese Quarterly of Mechanics，2005，26（1）：87-95.

［6］赵士清，张镜潮.连云港潮流的数值模拟［J］.海洋学报，1981，3（3）：500-515.

ZHAO S Q，ZHANG J C.Numerical simulation of current in Lianyungang［J］.Acta Oceanologica Sinica，1981，3（3）：500-515.

［7］Van R L C.Handbook of Sediment Transport by Currents and Waves［R］.Netherlands：Delft Hydraulics，1989.

［8］JIANG G S，WU C C.A high-order WENO finite difference scheme for the equations of ideal magnetohydrodynamics［J］.Comput.Phys.，1999，150：561-594.

［9］WEN L，James T K，ZHI Y S.A numerical scheme for morphological bed level calculations［J］.Coastal Engineering，2008，55：167-180.

［10］Colombini M，Seminara G，Tubino M.Finite-amplitude alternate bars［J］.Fluid Mech，1987，181：213-232.

［11］Schielen R，Doelman A，Swart H E D.On the nonlinear dynamics of free bars in straight channels［J］.Fluid Mech，1993，252：325-356.

Numerical model of morphology instability under flow

WANG Ming-ming，ZOU Zhi-li
（State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian116024，China）

The interaction between flow and topography may result in different forms of complex morphologies in the river，and alternate bars are one kind of these morphologies.Researches show that the corresponding formation mechanism is the instability of the bottom topography.In this paper,numerical simulation method and results of alternate bars caused by the bed instability were presented.The ADI scheme was implemented to solve the flow equation，and the equation for bed level change was solved by Euler-WENO scheme，which was more stable than the traditional schemes.This coupled computation model of flow and bottom morphology was used to study the evolution of the straight channel with alternate bars.

bed evolution；nonlinear；WENO；instability

P 731.23；O 242.1

A

1005-8443（2011）06-0389-10

2011-05-09；

2011-06-08

国家自然科学基金项目（51079024）；辽宁省教育厅高等学校自然科学基金

王明明（1986－），男，河南省禹州人，硕士研究生，主事海岸及近海工程的研究。