The maximum entropy principle for radiation fields†

GU Qiao

1)International Institute of Quantum Biology Haßloch 67454 Germany

2)College of Electronic Science and Technology Shenzhen University，Shenzhen 518060 P.R.China

The maximum entropy principle for radiation fields†

GU Qiao1，2

1)International Institute of Quantum Biology Haßloch 67454 Germany

2)College of Electronic Science and Technology Shenzhen University，Shenzhen 518060 P.R.China

The maximum entropy principle discovered by Jaynes E T governs a search of the most reasonable probability assignment of stochastic variable，based on the measured data.One of the simplest applications of this principle lies in that all the thermodynamical relations are derived from the maximizing entropy of the system with energy as a single measured value.The maximum entropy principle is used then for the radiation field as a quantum system.Our results show that with an increase of the number of measurable quantities，the thermal field，the coherent states as well as the squeezed states are automatically introduced in turn;in particular，the dependence of all the properties of these radiation fields on the thermal noise is formulated quantitatively.The fundamental results obtained in this paper are expected to provide a basis for applications of the maximum entropy principle in some fields，such as quantum optics，quantum informatics，biophotonics，and related interdisciplinary science.

maximum entropy principle;the most reasonable probability assignment;thermodynamical relations;thermal field;coherent state with thermal noise;squeezed state with thermal noise;quantum optics;quantum informatics;biophotonics

1 The maximum entropy principle

The maximum entropy principle is discovered by Jaynes E T in 1957［1-2］.This is a general expression for conventional probability theory，classical thermodynamics，and statistical physics.All of the laws of classical thermodynamics，in particular，the concepts of heat and temperature，could be defined in terms of the maximum entropy principle.Entropy maximization is following an ordinary common sense and deeply connected with experimental reality.The mathematical formulations of maximum entropy principle are straightforward，with which many applications have been carrying out［3］.

1.1 Simple examples

Let us start with the simple example to elucidate the maximum entropy principle.If a measurement of three possible states gives average value 2 of the stochastic variablei(i=1，2，3)，let us ask then:what is the probability assignment of the measured values?Obviously，the probability assignment satisfying the measured data could not be unique;two possible assignments are shown in Fig 1.However，the most reasonable probability assignment may be unique.The maximum entropy principle governs a search of the most reasonable probability assignment of stochastic variable，based on the measured data.

Consider another example of tossing die.After tossing a die very large numberNof times，one finds that the every outcome of the die appearsN/6 times.The probability of appearance of every outcome ispi=1/6(i=1，2，…，6)，following the equalprobability principle.The average spot number is 3.5 then.

Fig.1 Two different distributions give the same average value 2.图1 平均值为2的两种不同分布

However，for a particularly made die the average number might be found to，for example，be 4.5，instead of 3.5.The reason that leads to such a result must be a more appearance of the outcomes with the higher spots(5 and/or 6).The natural question is what kind of probability assignmentpimay give rise average number 4.5.We have，evidently，to look for thepisuch that

whereN=4.5.A possible solution of(1)is indicated in Fig 2(a);we could takep4=p5=0.5，all otherspi=0.This agrees with the given data.But our common sense tells us it is not a reasonable assignment because that all others do not appear impossibly in practice.Fig 2(b)shows an assignment that agrees with the data and does not ignore any possibility.But it still seems unreasonable to give the casei=6 such exceptional treatment.A reasonable assignmentpimust not only agree with the data and must not ignore any possibility，but it must also not give undue emphasis to any possibility.Thepishould vary as smoothly as possible，in some sense.One criterion of“smoothness”might be that adjacent differencepi+1-pishould be constant;and there is a solution with that property.It is given bypi=(12i-7)/210 and shown in Fig 2(c).This is evidently the most reasonable probability assignment so far.However，with this linear variation ofpian average is limited by the assignmentpi=constant·(i-1).Actually，this extreme assignment not only ignores one possibility becausepi=0 but works out only 4.7 as the maximum average.Suppose the data of the problem had been changed so that the average is to be 4.7 instead of 4.5.Then there is no straight-line solution satisfyingpi＞0.One can imagine that thepimust lie on some concave curve.

After all，what is the most reasonable probability assignment satisfying(1)actually?In the maximum entropy principle，it should be an entropy maximizing distribution.This means that it results from maximizing entropy given by

with the constraints(1).We therefore maximizeSby the method of Lagrange multipliers.If we vary thepi's，the variation inSis

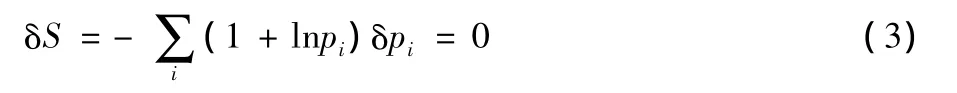
At the same time，the variations in the constraints(1)are

By the method of Lagrange multipliers，we have

Fig.2 The possible probability assignments in tossing die，with the same average spot number 4.5 and the different values of the entropy.图2 掷骰子平均点数为4.5时的可能几率分布与相应熵值

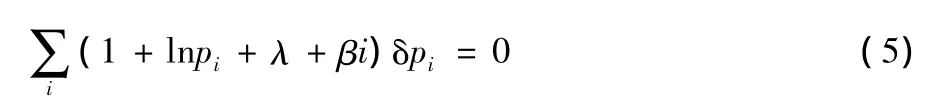
where λ and β are undetermined parameters.Then the distribution is exponential function

whereZ=exp(1+λ)and β are determined by(1)as the relations

From(7)we obtainZ=26.7 and β=0.371 forN=4.5.The exponential distribution(6)is shown in Fig 2(d).

With the help of the above examples one may get a preliminary knowledge on the maximum entropy principle.It is based on the given data in measurement of stochastic variableiand traces back the distribution oniby maximizing entropy.The entropy maximizing distribution is the most reasonable probability assignment in the sense.Such a probability assignment most honestly describes the given data.It is the most conservative assignment that it does not permit one to draw any conclusions unwarranted by the data.Formally，this assignment is as smooth and“spread out”as possible，thus it is，subject to constraints，most nearest to the probability assignment predicted by a normal equal-probability principle.

1.2 General formalism

We now consider a general measurement of a stochastic event obtainingnpossible states，wherencan be finite or infinite.It gives the average values ofmquantitiesf1(i)，f2(i)，…，fm(i)，whereicorresponds toith state(i=1，2，…，n).They are represented byF1，F2，…，Fm，wherem＜n.The problem is to find the probability assignmentpiwhich satisfies the given data:

where we have put Boltzmann constantkin order to agree with the thermodynamical notation.Using the method of Lagrange multipliers，we obtain probability distribution

where the λ's are Lagrange multipliers andZis the partition function defined by

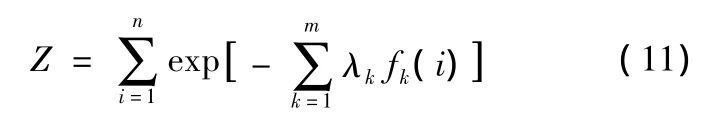
Then the entropy(9)is represented by

The Lagrange multipliers are related to the given data by the equation

The higher moments are given by

Above expressions provide all the results of the maximum entropy principle for a general measurement.

1.3 Boltzmann distribution

We now apply the above-mentioned formalism to the simplest situation:m=1 andf1(i)=Eibeing the energy of the system.The average value of the energy，〈Ei〉≡U，is given as the data.The partition function is

where we have，in particular，set λ1=β.With this we may write a number of the previous formulas in a way which can be immediately identified with relations well known in thermodynamics.Instead of(10)we find

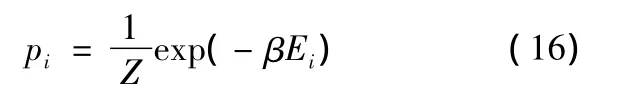
which is the well-known Boltzmann distribution. Then， by(13)，β is determined by

Equation(12)gives

By comparison with the thermodynamic expression

whereTis the absolute temperature，we recognize in(18)thatUis the internal energy and 1/β=kT，and the free energyFis represented by

One can see that a series of the thermodynamic expressions have been worked out.A number of further identities of thermodynamics can easily be checked by applying the above formulas［4］.

The above-mentioned maximum entropy principle is associated with the classical entropy(2).In the subsequent sections we will show how to use this principle for radiation field as a quantum system.One will see that with an increase of the given data，the thermal field，the coherent states as well as the squeezed states can be introduced automatically.The maximum entropy principle applied to radiation field may open a lot of new knowledge which has not only academic but practical significance.

2 Radiation field in thermal equilibrium

Entropy of a quantum system is written with substitution of the probability distribution by the density operator and of the summation by the trace.Thus we have from(2):

subject to the constraint

The diagonal matrix elements of ρ are real and positive in any representation.In particular，the density operator ρ may have an eigenequation

With(23)we can evaluate the trace in the representation{

whereRiis an eigenvalue，which represents the probability of finding the system in the eigenstate〉}，so that entropy of the quantum system is written in the classical form［5］

Like the classical case，the entropy(21)is a measure of lack of knowledge about the states of the system.For if we maximizeSsubject to(22)，just as in the classical case，we find

yielding ρ=constant，so thatRi=constant.This tells us that the probability of finding the system in any of its possible states is the same when the entropy is a maximum.Thus，we have no knowledge about the states of the system.On the other hand，if we know the state of the system precisely，i e，we know that the system is in a pure state〉，thenS=0 sinceRi=δij.

Let us consider a single-mode radiation field in thermal equilibrium with the heat bath at temperatureT，and we now suppose that we know something about it，for example，its average energy.The average energy is

whereHis the Hamiltonian for this mode，given by

in whichaanda+are the annihilation and creation operators of a photon，ω is the frequency of this mode，and ħ Planck constant divided by 2π.

Following the procedure of the maximizing entropy for a classical system，we will maximize the entropy(21)subject to the constraints(22)and(26)in order to find the most reasonable density operator.For this purpose，we vary:

Multiplying the second of these by the undetermined multiplier λ0and the third by β and adding to the first，we have

Since δ ρ is arbitrary and all variations are now independent，this will be satisfied if and only if

This gives

whereZ=exp(1+λ0)is the partition function，which is determined by(22)as

This may be written，using(27)，as

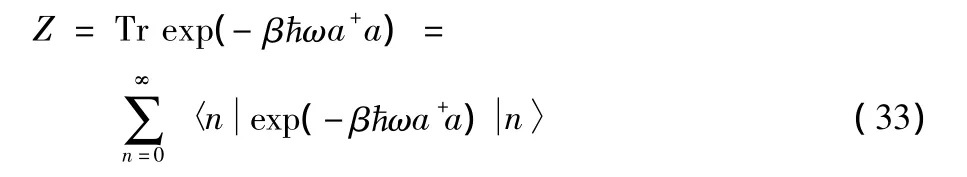
where we have taken the trace in the number representation〉}.By the use ofa+〉=〉，the sum in(33)can be carried out，yielding

In order to determine the parameter β，we use the constraint(26)and obtain

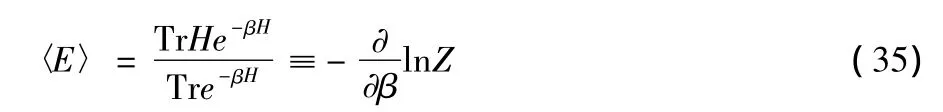
This becomes，using(34)，that

It is easy to solve for β in terms of〈E〉.However，from the correspondence principle，as→0 the average energy〈E〉must become the average classical energy contained in a field mode;that is，〈E〉→kTas→ 0 since from the classical equipartition-ofenergy theorem，we getkT/2 per degree of freedom.The electric and magnetic fields each correspond to one degree of freedom.Actually，the limit of(36)as→ 0 gives that〈E〉→ 1/β，so that β=1/kT.Thus the average energy(36)becomes

This is just the Plank distribution law for blackbody radiation.We have seen that the most reasonable distribution predicted by the maximum entropy principle is just the well-known natural law.Thus we obtain the completely determined density operator

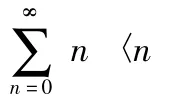
We now express the density operator in terms of the average photon number.Essentially，the density operator has the photon number operatora+aas its key.We write(38)，using(27)，as

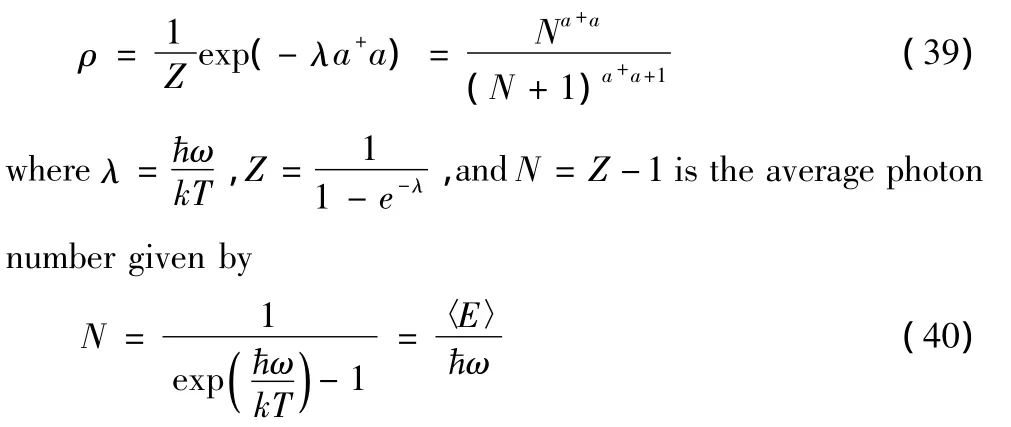
The dependence of the average photon number in the thermal field on the frequencyv(or to the wavelength λ)and temperatureTis plotted in Fig 3，which provide a basic concept for estimating the influence of them on the total intensity of a practical radiation field.

We now compute the entropy of the field mode based on(38).For this purpose，we insert the completeness relation in the number representation to the right side of(39)，we get density operator in the form

Fig.3 The curves in(a)may be used to estimate the influence of the thermal noise of a detector on the radiation of photon emission from biological systems［6］and the curves in(b)for the microscopic wave radiation from the one-atom maser system［7-8］.图3 热场平均光子数随波长及温度的变化.(a)图中曲线用来估算热噪声对生物系统光子辐射的影响［6］，(b)图中曲线用于单原子系统微波辐射的实验研究［7-8］.

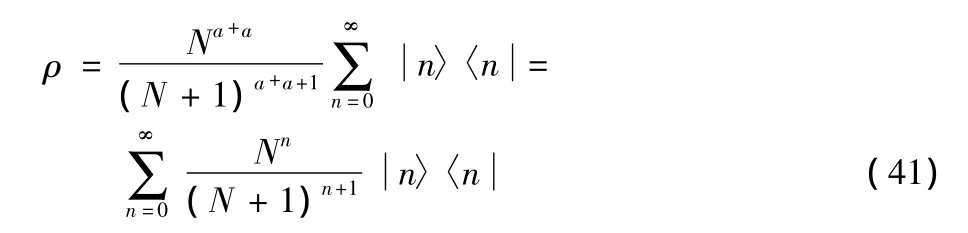
It is straightforward to get the entropy of the radiation field.Since the density operator(41)has the number states〉as its eigenstates，the entropy therefore has the classical form(24)，that is［5］

Furthermore，we investigate the photon statistical properties of the field.For this purpose，we use(41)for obtaining the photon number distribution

The normalized factorial moments are then

In particular，the variance in the photon number is

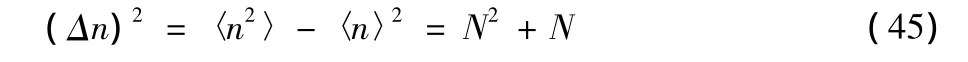
and the second-order correlation function is

Equation(44)shows a rapid increase of the normalized factorial moments with the order numberkfor a single-mode thermal field.This may provide a tool to identify such a field by means of the measurement of photocount distribution.It has been used for investigation of the properties of the organic materials［9］，where a weak photon emission of the materials is measured as a signal.

Finally，we use the dimensionless quadrature operators［10］:

to describe the field fluctuation represented by［11］

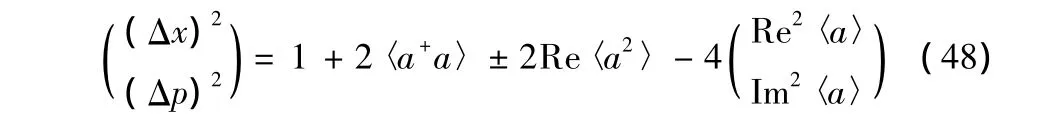
where the expectation values〈…〉are taken in any representations.We now calculate the field fluctuations，using the density operator(39).Actually，we have

and〈a2〉=0 at the same time，so that

It shows that the field fluctuations increase linearly with the average photon numberN.In the limiting caseN→0 asT→0，the field reduces to a vacuum state，being a special case of the coherent states since(Δx)2=(Δp)2=1 from(50)and(Δn)2=0 from(45).Note that a vacuum can also be a special number state or a special chaotic state.

We have discussed the thermal field from the different points of view.In this section the density operator is obtained by maximization of entropy with，in addition to(22)，one constraint(26).We will see that with increase of the given constraints the radiation field with more information content may be introduced out.

3 Coherent states with thermal noise

We use the maximum entropy principle to determine the density operator which describes a more of the radiation field when we have made various measurements.Let us assume that we measure，in addition to the average energy，the average electric and magnetic field of the mode.We therefore have

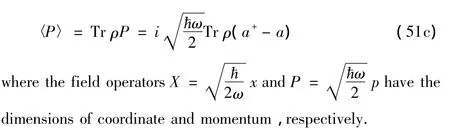
Following the procedure for the thermal field case，we maximize the entropy(21)subject to the constraints(22)and(51)，we have，instead of(29)，on using Lagrange multipliers

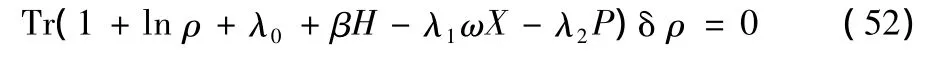
This will be satisfied by

The complex Lagrange parameter γ1results from π /2 out of phase between〈X〉and〈P〉.Let us introduce the new operators

where we have ignored the uninterestingc-numberWe see from(55)that［b，b+］=1，sobandb+may be interpreted as the quasiboson annihilation and creation operators，so we may establish a“number”representation〉b}

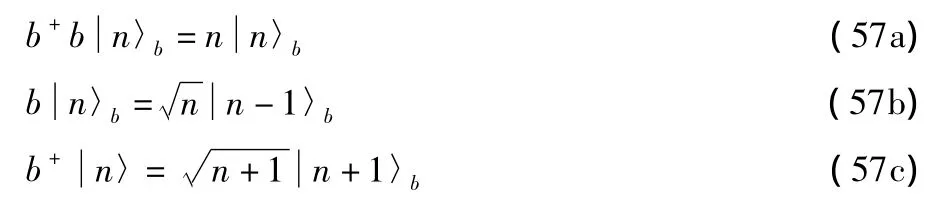
Thus the trace for(56)may be calculated in the representation{〉b}and the partition functionZis obviously the same as that in the thermal field，represented by(34).Also，we have from(55)that

We must next determine the Lagrange multipliers λ，wandw*.For this purpose，we substitute(56)into(51a)，calculating the trace in the representation{〉b}and using(57)，we obtain

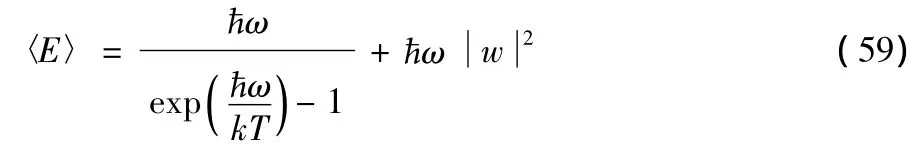
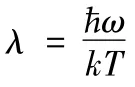
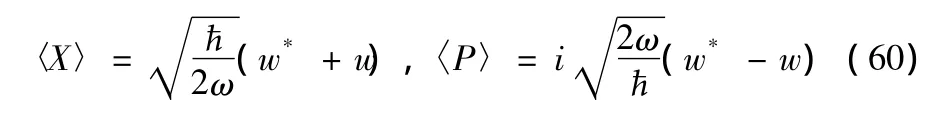
makew1andw*directly expressible in terms of the average of the electric and magnetic field.

The radiation field under consideration displays such an average energy that is added to that of the thermal field by the term.It suggests the average photon number in the field mode

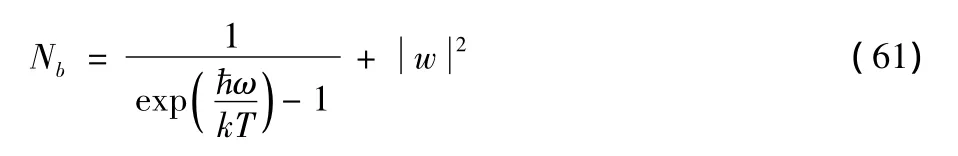
Let us consider first the case in which only thermal radiation occurs with the bath at temperatureT.Then the average electric and magnetic fields are zero:

so that we have from(58)thatb+b=a+a.Thus the density operator(56)obtained here reduces to(41)，corresponding to pure thermal noise，as discussed in detail in the last section.On the other hand，asT→0 the average energy(59)becomes

We now calculate the entropy of the radiation field containing the signal and the noise.Since the density operator(56)has the number states〉bas its eigenstates，we have

which is exactly the same as that of the thermal field，depending onlyNas the average photon number of the thermal field，instead ofNb.This means that the additional measurements produce only the additional energy，no additional entropy.Actually，we have known that the additional field is a coherent state with zero entropy.

We now turn to discuss the photon statistical properties of the present field.By using(56)，the photon number distribution is

and the normalized factorial moments are then

where Laguerre polynomials are given by the power series

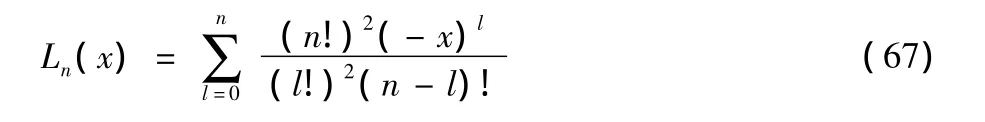
Obviously，(65)involves the contributions of the signal and the noise，demonstrated byandN，respectively.In the pure noise case(=0)，Eq(67)has only the first term(corre-sponding tol=0)to be non-zero:Ln(0)=n!，so that(65)and(66)reduce respectively to(43)and(44)as the results of the thermal field.On the other hand，for the pure signal case(N=0)，after moving the factorNn/(N+1)n+1in(65)into the sum，we see that the present summation has only the last term(corresponding tol=n)to be non-zero，carrying outThus the photon number distribution becomes Poissonian

Similarly，(66)reduces to

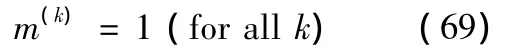
These show the well-known results for coherent states［12］.For the general signal plus noise case，the photon number distribution(65)and the normalized factorial moments(66)are plotted in Fig 4 and Fig 5，respectively.

Fig.4 The photon number distribution(65)of the coherent state with thermal noise.图4 存在热噪声的相干态光子数分布.见式 (65)

We now discuss the field fluctuations in terms of the dimensionless quadrature operatorsxandp.We have from(60)that

Also，we write〈x2〉=Trρ(a++a)2and〈p2〉=-Trρ(a+-a)2，by(55)and(56)，as

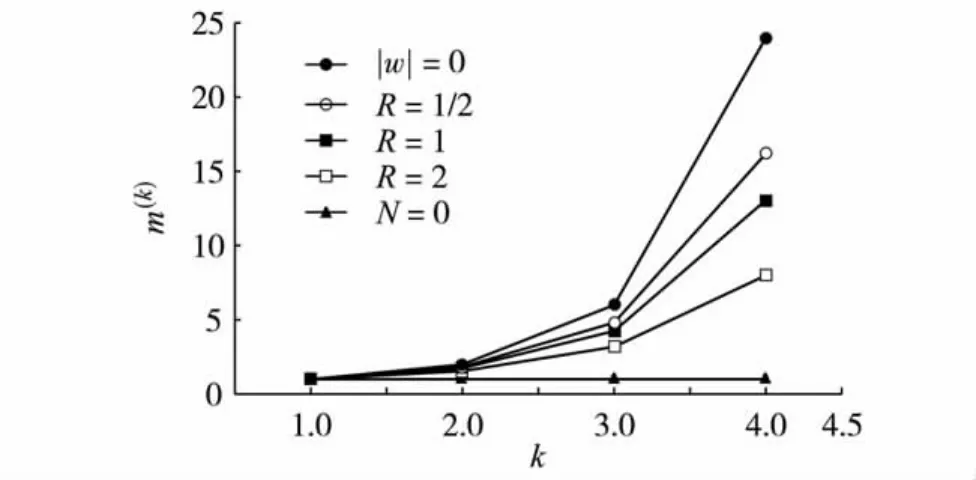
Fig.5 The normalized factorial moments(66)of the coherent state with thermal noise，for the different values of the ratio R≡/N.图5 不同R值时 (R≡/N)包含热噪声的相干态归一化阶乘矩.见式 (66)

which shows that the field fluctuations increase linearly with the noise photon numberN，independent of the signal photon number，same as(50)for the thermal field.Similarly to the behavior of entropy，the additional measurements do not produce any additional field fluctuations.In the pure signal case(N=0，≠0)，the field reduces to a coherent state，which is a minimum-uncertainty state defined by ΔxΔp=1 and has equal uncertainties in the two quadratures:

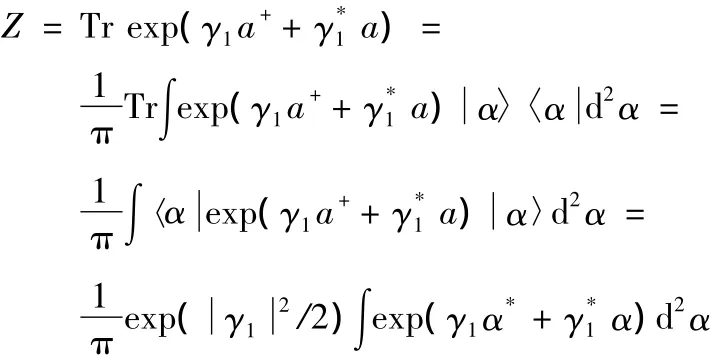
The resulting integral leads to a singularZ，meaning that no corresponding density operator occurs.We conclude therefore that it is necessary anyway to use the energy constraint.

In summary the following points should be emphasized.①The maximization of entropy for a radiation field，with given value of the average energy and additionally given values of the average electric and magnetic fields，determines a density operator which describes a coherent state as a signal accompanied with the thermal noise.② A pure coherent state could not occur individually without the thermal noise unless at zero temperature.The total energy of the field is a sum over the signal and the noise.③ The additional field as a pure state does not induce additional entropy and field fluctuations.It essentially suggests that entropy and field fluctuations play equivalent roles in description of the quantum statistical properties of the radiation field.

At the conclusion of this section，it may be interesting to mention the different ways in which the concept of coherent state is defined.As it is well known that the coherent states are introduced normally as the eigenstates〉of the annihilation operatoraor by an action of the displacement operatorD(α)=exp(αa+-α*a)to the vacuum state〉，that is〉=D(α〉.In a way completely different from these，the coherent states have been introduced here by maximization of entropy for radiation field subject to the constraints on the energy and the fields.Moreover，a coherent state is found to not occur on its own，instead it is encircled always by the noise in practice.This is quite a novel fact from which the maximum entropy principle is shown to be really of a general and fundamental significance.It gives the most reasonable(hence the most reality)density operator to describe a knowledge state about the physical situation.It may be imagined that some further states obtaining more information could be introduced if more measurable quantities have the given values.

4 Squeezed states with thermal noise

A squeezed state is known to have less field fluctuation in one quadrature than a coherent state.To satisfy the requirements of the uncertainty relation，the field fluctuation in another quadrature must be greater than that of coherent state.So a squeezed state is characterized by Δx＜1＜Δpor by Δp＜1＜Δx.Squeezed states are defined as the eigenstatesof the combined operatorb=μa+va+，where the complex parameters μ，vsatisfyand the uncertainties areand

These reduce to Δx=exp(-r)and Δp=exp(r)if θ=0，which describe a minimum-uncertainty state but have in general the unequal uncertainties in the two quadratures.Asr=0 this state becomes to a coherent state:Δx=Δp=1.

Above definitions of squeezed states are based on quite deep a knowledge on quantum optics［13-18］.We will introduce the squeezed states by means of the maximum entropy principle;it is straightforward，where we only need to express more measurable quantities with the given values.

Let us consider first the Hamiltonian［13］

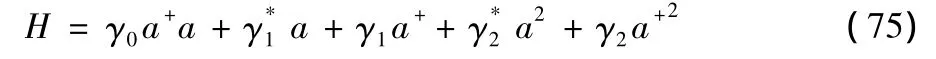
where γiare thec-numbers.From Hermiticity γ0has to be real.The γ1and γ2terms describe the one-photon and two-photon mechanism，respectively.

where γ is real，with the same sign as γ0，and has absolute value

and the operatorsc，c+and thec-numberCare defined by

respectively，with μ，vbeing complex and taking the form

where 2θ and φγare the phases of γ2and γ，respectively:.The canonical transformation(78)is an inhomogeneous linear one.Similar to the operatorsbandb+represented in(55)，we see［c，c+］=1，so we may again establish a“number”representation{〉c}，which satisfies the relations as(57).The Hamiltonian(76)is manifestly positive definite，which likes a free single-mode field(or a harmonic oscillation)apart from an unimportantc-numberC.

Considering a measurement for a radiation field，we assume that，in addition to the energy and fields，we also have the measured values of square of the electric and magnetic fields.Totally we have the following measured values:

Subject to these constraints and(22)we will maximize entropy(21).Following the previously used method，we have，instead of(52)，that

which will be satisfied by

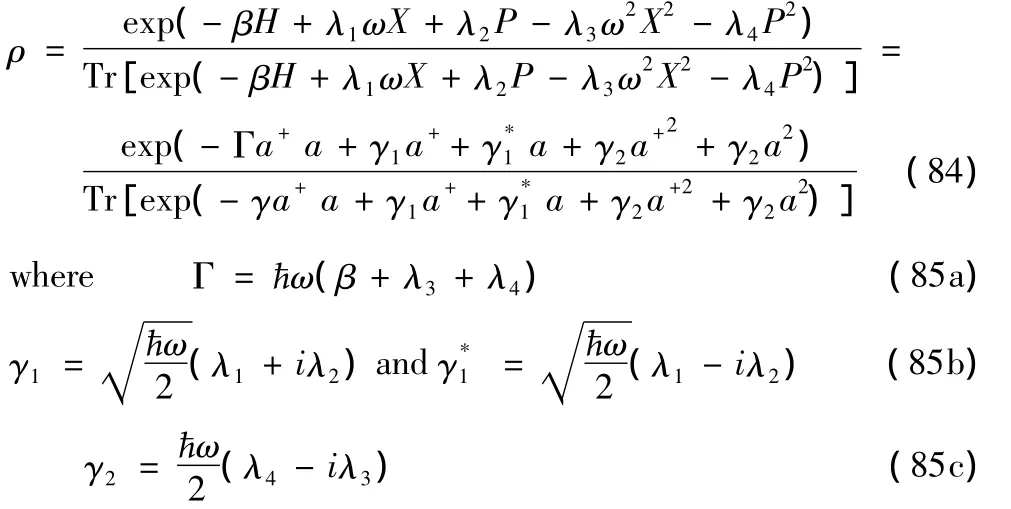
Note that the Lagrange parameter γ2appearing in(84)，given by(85c)，is real since the measured values〈X2〉and〈P2〉are found to be π out of phase.Obviously，if one measures the cube of the electric and magnetic fields，the corresponding Lagrange parameter must be complex since the average values〈X3〉and〈P3〉are 3π/2 out of phase.

Thus the linear transformation(78)can be written for any values of γ2as

where thec-numberWandW*are defined by

The density operator(84)takes then the form

where the partition functionZcis calculated in the representation{〉c}，yieldingEquation(89)displays a general solution of density operator under the measured data(82).Whenr=0(W→w)，the canonical transformation(86)reduces to(55)，and Λ→λ，Zc→Z，so the density operator(89)reduces to(56)，that is the case on coherent state with thermal noise.The parameterrresulting from the two-photon effect is related to the coefficient γ2given by in(88b).We plotras a function of the real number γ2/Γ in Fig 6.

Fig.6 The parameter r as a function of the real number γ2/Γ，where r changes from+∞ to-∞ as γ2/Γ changes from-1 to+1.图6 参数r随γ2/Γ的变化曲线.其中当γ2/Γ从-1到+1变化时，r在+∞到-∞之间变化.

We have from(86)that

By(91)，the average energy〈E〉=ħω〈a+a〉is calculated in the representation{〉c}，yielding

which satisfies the limiting condition〈E〉→kTasT→0，the frequency Ω is defined by Ω = ωcosh2r.The average number of photon is then

where sinh2r+is known to be the number of photons in a normal squeezed state，and the first term is the number of photons originating from the thermal noise.Obviously，we work out a squeezed state with thermal noise.Whenr=0，Nc→Nb［see(61)］.it is the result of the coherent state with thermal noise.Furthermore，in terms of

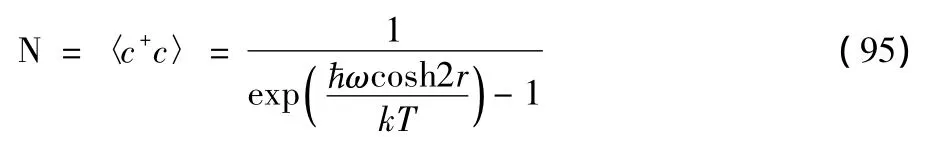
the entropy of the radiation field is represented as

which is dependent of temperatureTand the squeezing factorr，but independent of the coherent component.The dependence of this entropy onis shown in Fig 7.For the larger，the entropy approaches to zero，so that the radiation field approaches to a pure state.On the other hand，whenr=0(N →N)，this entropy reduces to that on the coherent state with thermal noise，where the entropy is determined by a pure thermal noise(40).

Fig.7 The entropy of the squeezed state with thermal noise，as a function of:(a)for the given wavelength and the different values of temperature;(b)for the given temperature and the different values of frequency.图7 存在热噪声时压缩态的熵随的变化.(a)给定λ，T不同;(b)给定T，v不同.

Let us next discuss the fluctuations of the field.By(91)，we obtain

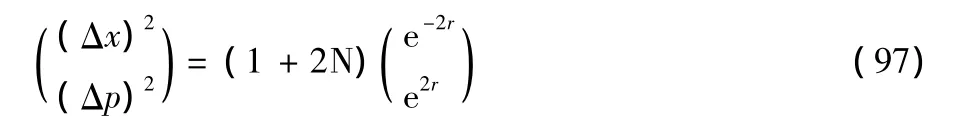
Unlike the normal squeezed state where thex-quadrature exhibits always squeezing forr＞0 and thep-quadrature exhibits always squeezing forr＜0，the present state shows squeezing inxorpcomponent under conditions

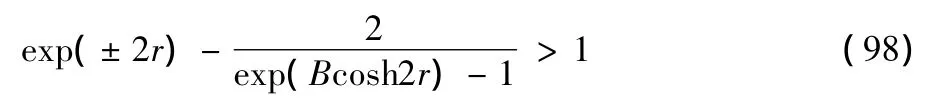
①thex-quadrature fluctuation atr=0 depends on the value of the factorB:the largerB，the lower fluctuation，which approaches to unit asB→∞;

②this fluctuation decreases monotonically with increasingrand behaves as function exp(-2r)，approaching to zero asr→∞for any of the values ofB;

③p-quadrature increases monotonically with increasingrand behaves as function exp(2r)，becoming infinite asr→∞ for any of the values ofB.

Fig.8 The field fluctuations in the squeezed state with thermal noise change as a function of r(r＞0).图8 存在热噪声时压缩态场起伏随r(r＞0)的变化

In short，for largerBorr，so that N→0，the present state becomes a normal squeezed state with Δx=e-rand Δp=er.On the other hand，whenr=0，Eq(97)reduces to(50)as the result on the coherent state with thermal noise.Also，whenr=0 andT→ 0 it results in a normal coherent state with Δx=Δp=1.We should emphasize here that both of the entropy shown in Fig 7 and the field fluctuation in Fig 8(a)decrease with increasingr.This means that the entropy may work as a measure of the field fluctuation［5］.This is really useful in analysis of coherence properties of a practical radiation field.

Conclusion

The maximum entropy principle is following an ordinary common sense.It is based on the given data in measurement of stochastic variableiand traces the distribution oni.In principle，the distribution satisfying measured data could not be unique，but the most reasonable one is unique in practice.Such a probability assignment most honestly describes the given data.It is the most conservative assignment that it does not permit one to draw any conclusions unwarranted by the data.Formally，this assignment is as smooth and“spread out”as possible，thus it is，subject to constraints，most nearest to the probability assignment predicted by a normal equal-probability principle.One of the simplest applications of this principle lies in that all the thermodynamical relations are derived from the maximizing entropy of the system with energy as a single measured value.The maximum entropy principle has been used then for radiation field as a quantum system.Our results show that with an increase of the number of measurable quantities，the thermal field，the coherent states as well as the squeezed states are automatically introduced in turn;in particular，the dependence of all the properties of these radiation fields on the thermal noise is formulated quantitatively.The fundamental results obtained in this paper are expected to provide a basis for applications of the maximum entropy principle in some fields，such as quantum optics，quantum informatics，biophotonics，and related interdisciplinary science［19-24］.

A further research with additional given data of〈X3〉and〈P3〉is in preparation，which is expected to work out a novel quantum state of radiation field.

† This work was supported as a special project by International Institute of Quantum Biology，Germany.

［1］Jaynes E T.Information theory and statistical mechanics［J］.Physics Review，1957，106(4):620-630.

［2］Jaynes E T.Information theory and statistical mechanics:II［J］.Physics Review，1957，108(2):171-190.

［3］Jaynes E T.Where do we stand on maximum entropy?［G］//Levine R D，Tribus M.The Maximum Entropy Formalism.Cambridge:The MIT Press，1978:15-118.

［4］Haken H.Information and Self-Organization:A Macroscopic Approach to Complex Systems［M］.Berlin:Springer-Verlag，1988.35-76.

［5］GU Qiao.Quantum entropy of radiation fields［J］.Journal of Shenzhen University Science and Engineering，2011，28(2):95-104.

［6］Mieg C，Mei W P，Popp F A.Technical notes to biophoton emission［C］//Popp F A，Li K H，GU Qiao.Recent Advances in Biophoton Research and Its Applications.Singapore:World Scientific，1992:197-205.

［7］Rempe G，Walther H.Observation of quantum collapse and revival in a one-atom maser［J］.Physical Review Letters，1987，58(4):353-356.

［8］GU Qiao.Squeezing in one-atom maser［J］.Chinese Journal of Lasers，1990，17(6):347-351.(in Chinese)

［9］Popp F A.Some essential questions of biophoton research and probable answers［C］//Popp F A，Li K H，GU Qiao.Recent Advances in Biophoton Research and Its Applications.Singapore:World Scientific，1992:1-46.

［10］ GU Qiao.Squeezing in a two-photon Jaynes-Cummings model［J］.Acta Physica Sinica，1988，37(5):751-759.(in Chinese)

［11］GU Qiao.The quantum statistical properties of the Jaynes-Cummings model［J］.Acta Physica Sinica，1989，38(5):735-744.(in Chinese)

［12］Glauber R J.Coherent and incoherent states of the radiation field［J］.Physics Review，1963，131(6):2766-2788.

［13］ Yuen H P.Two-photon coherent states of the radiation field［J］.Physics Review，1976，A13(6):2226-2243.

［14］Caves C M.Quantum-mechanical noise in an interferometer［J］.Physical Review D，1981，23(8):1693-1708.

［15］GU Qiao.Novel features in photon statistics from a singlemode laser ［J］.Science in China:English edition，1990，A33(9)，1460-1468.

［16］GU Qiao，ZHANG Ji-yue.A possible way for generating sub-poissonian field ［J］.Acta Optica Sinica，1989，5(5):478-480.(in Chinese)

［17］GU Qiao.Photon statistics for laser with a weak spontaneous emission ［J］.Journal of Shenzhen University Science and Engineering，1990，7(1/2):11-20.(in Chinese)

［18］Walls D F，Milburn G J.Quantum Optics［M］.Berlin:Springer-Verlag，1994，1-72.

［19］GU Qiao.The ultraweak photon emission from biological systems(review)［J］.Quantum Electronics，1988，5(2):97-108.(in Chinese)

［20］Aoki I.Entropy flow and entropy production in the human body in basal conditions［J］.Journal of Theoretical Biology，1989，141(1):11-21.

［21］Aoki I.Effects of exercise and chills on entropy production in human body ［J］.Journal of Theoretical Biology，1990，145(3):421-428.

［22］Aoki I.Entropy principle for human development，growth and aging［J］.Journal of Theoretical Biology，1991，150(2):215-223.

［23］GU Qiao，Popp F A.Nonlinear response of biophoton e-mission to external perturbations(review)［J］.Experientia，1992，48(11/12):1069-1082.

［24］GU Qiao.Biophotonics［M］.Beijing:Science Press，2007:1-18.(in Chinese)

参考文献:

［1］Jaynes E T.信息论与统计力学 ［J］.物理评论，1957，106(4):620-630.(英文版)

［2］Jaynes E T.信息论与统计力学 II［J］.物理评论，1957，108(2):171-190.(英文版)

［3］Jaynes E T.我们应该研究的最大熵原理是什么?［G］//Levine R D，Tribus M.最大熵原理.剑桥 (美国):麻省理工学院出版社，1978:15-118.(英文版)

［4］Haken H.信息与自组织:一种多元系统的宏观处理［M］.柏林:施普林格出版社，1988.35-76.(英文版)

［5］顾 樵.辐射场的量子熵 ［J］.深圳大学学报理工版，2011，28(2):95-104.(英文版)

［6］Mieg C，Mei W P，Popp F A.生物光子辐射的技术问题［C］//Popp F A，Li K H，顾 樵.生物光子学及其应用研究进展.新加坡:世界科学出版社，1992:197-205.(英文版)

［7］Rempe G，Walther H.单原子微波激射器中的量子塌陷与再生 ［J］.物理评论快报，1987，58(4):353-356.(英文版)

［8］顾 樵.单原子微波激射器中的压缩［J］.中国激光，1990，17(6):347-351.

［9］Popp F A.生物光子学的一些根本问题及其可能答案［C］//Popp F A，Li K H，顾 樵.生物光子学及其应用研究进展.新加坡:世界科学出版社，1992:1-46.(英文版)

［10］顾 樵.双光子Jaynes-Cummings模型中的压缩 ［J］.物理学报，1988，37(5):751-759.

［11］顾 樵.Jaynes-Cummings模型的量子统计特性 ［J］.物理学报，1989，38(5):735-744.

［12］Glauber R J.辐射场的相干态与非相干态 ［J］.物理评论，1963，131(6):2766-2788.(英文版)

［13］Yuen H P.辐射场的双光子相干态 ［J］.物理评论，1976，A13(6):2226-2243.(英文版)

［14］Caves C M.干涉仪的量子力学噪声 ［J］.物理评论D，1981，23(8):1693-1708.(英文版)

［15］顾 樵.单模激光光子统计的新特征 ［J］.中国科学:英文版，1990，A33(9):1460-1468.(英文版)

［16］顾 樵，张纪岳.一种产生亚泊松光场的可能途径［J］.光学学报，1989，5(5):478-480.

［17］顾 樵.弱自发辐射激光的光子统计特性 ［J］.深圳大学学报理工版，1990，7(1/2):11-20.

［18］Walls D F，Milburn G J.量子光学 ［M］.柏林:施普林格出版社，1994:1-72.(英文版)

［19］顾 樵.生物体系统的超微弱光子辐射 (综述)［J］.量子电子学，1988，5(2):97-108.

［20］Aoki I.一般情况下人体的熵流及熵产生 ［J］.理论生物学，1989，141(1):11-21.(英文版)

［21］Aoki I.运动与寒冷对人体熵产生的影响 ［J］.理论生物学，1990，145(3):421-428.(英文版)

［22］Aoki I.人体成长及衰老过程中的熵原理 ［J］.理论生物学，1991，150(2):215-223.(英文版)

［23］顾 樵，Popp F A.生物光子辐射对外界微扰的非线性响应 ［J］.实验，1992，48(11/12):1069-1082.(英文版)

［24］顾 樵.生物光子学 ［M］.北京:科学出版社，2007:1-18.

2011-04-11

德国国际量子生物学研究所专项基金资助项目

顾 樵(1947-)，男 (汉族)，陕西省西安市人，德国国际量子生物学研究所首席科学家、深圳大学教授.E-mail:gu-qiao@gmx.de

辐射场的最大熵原理

顾 樵1，2

1)德国国际量子生物学研究所，Haßloch，67454，德国;2)深圳大学电子科学与技术学院，深圳518060

Jaynes E T的最大熵原理指出如何从随机变量的测量数据推导出最合理概率分布.该原理最直接的应用是给出了所有热力学关系，这是对具有能量作为单一测量值的经典系统进行熵的最大化处理的结果.本研究将最大熵原理推广到量子力学系统，揭示辐射场的量子统计性质.结果显示，随着可测量力学量类别的增加，依次自动引出混沌态、相干态和压缩态等一系列辐射场态.值得关注的是运用该方法，所有辐射场态对热噪声的依赖性可被定量描述.该研究结果有望用于量子光学、量子信息学、生物光子学及相关交叉学科领域.

最大熵原理;最合理概率分配;热力学关系;热场;热噪声相干态;热噪声压缩态;量子光学;量子信息学;生物光子学

O 431.2

A

1000-2618(2011)04-0294-CA

O 431.2

A

Abstract:1000-2618（2011）04-0283-12

【中文责编:方 圆;英文责编:卫 栋】