基于梁柱单元的钢筋混凝土桥墩地震损伤分析

李 正，李忠献

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072)

基于梁柱单元的钢筋混凝土桥墩地震损伤分析

李 正1,2，李忠献1,2

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072)

Faria-Oliver模型是一个简单而有效的混凝土损伤模型.基于 Faria-Oliver模型提出了混凝土单轴损伤模型，且加以修正以更好地模拟混凝土单边效应；在 ABAQUS软件平台上，编制了含有钢筋修正 Menegotto-Pinto模型和混凝土单轴修正Faria-Oliver损伤模型的用户材料子程序VUMAT，建立了纤维模型等效模拟方法；分别模拟了一钢筋混凝土桥墩试件的循环加载试验和一钢筋混凝土桥墩试件的振动台试验，模拟结果与试验结果基本吻合.研究表明：本文所给出的单轴本构模型及纤维模型等效模拟方法有效、适用；基于梁柱单元的钢筋混凝土桥墩地震损伤分析不仅计算效率高而且提供了地震损伤演化过程信息，具有较强的工程实用性.

钢筋混凝土桥墩；地震损伤；单轴损伤本构模型；梁柱单元；纤维模型

地震非线性动力分析是目前钢筋混凝土桥梁抗震设计的重要手段.钢筋混凝土桥梁结构建模是进行非线性动力分析的前提.目前对钢筋混凝土桥梁结构的建模方式可分为两大类.①实体建模[1-2]，即钢筋用梁单元或杆单元模拟，混凝土用实体单元模拟，钢筋与混凝土的相互作用通过接触或界面单元进行模拟.这种方法能够全面考虑钢筋混凝土结构的各种效应，但地震作用下的混凝土本构模型、裂缝模拟、钢筋与混凝土相互作用模型等问题仍需进一步研究，同时对于大型钢筋混凝土结构，地震非线性动力分析计算成本十分巨大.②采用杆系模型即梁柱单元模型[3-7]，目前常用的有集中塑性模型、多弹簧模型和纤维模型等.纤维模型从材料层次自然地考虑了轴力与双向弯矩的相互作用，实现了模拟精度与计算效率的平衡.同时，纤维模型只需要钢筋与混凝土两种材料的单轴本构模型，而单轴本构模型的研究相对多轴模型更为成熟、模型精度也更高.另一方面，混凝土损伤模型是目前混凝土本构模型领域的研究热点之一，损伤模型通过引入损伤内变量，能较好地模拟混凝土材料特有的各种力学行为，同时能给出损伤演化过程，便于设计人员识别结构的薄弱部位，预测结构的潜在失效模式.因此，将混凝土单轴损伤模型与梁柱单元纤维模型结合便能快速地对大型混凝土结构进行地震损伤分析，具有较强的实用性.

Faria-Oliver模型是一个简单而有效的多轴混凝土损伤模型[8]，但由于其在描述混凝土单边效应方面效果欠佳，笔者尝试将其修正并基于修正的多轴Faria-Oliver混凝土损伤模型提出了单轴损伤模型，进而基于ABAQUS显式分析模块提供的用户材料子程序接口 VUMAT自编了混凝土单轴修正 Faria-Oliver损伤模型与钢筋的修正 Menegotto-Pinto模型子程序[5]，利用纤维模型的等效模拟方法[9-10]，对混凝土桥墩的循环加载试验与振动台试验进行了数值模拟，模拟结果良好，从而初步验证了纤维模型等效模拟方法与单轴本构模型的有效性，为大型钢筋混凝土桥梁结构地震响应及损伤分析奠定了基础.

1 混凝土单轴损伤模型

1.1 损伤准则

混凝土拉、压等效有效应力分别定义为

1.2 内变量演化方程

本模型的内变量包括损伤变量与塑性应变.为了反映混凝土拉、压损伤异性，分别用d+、d-描述拉、压损伤.拉、压损伤变量演化方程[8]为

假定塑性变形仅与混凝土受压行为相关，受拉卸载无塑性应变产生.单轴塑性应变p演化方程为

式中：β为材料塑性参数；H (·)为Heaviside函数.

1.3 修正的总应力表达式

根据连续损伤力学原理，单轴有效拉应力与有效压应力可分别表示为

在循环荷载作用下，混凝土存在单边效应.当从拉到压时，由于受拉裂纹闭合，刚度会发生完全恢复；而从压到拉时，由于受压损伤属于压碎性破坏，刚度不能完全恢复[11-12].原模型对从压到拉的单边效应描述欠佳，本文引入刚度影响因子s，考虑受压损伤对受拉刚度的影响.修正的单轴总应力σ表达式为

式中：() 为 Macaulay括号，即 x = ( x + x)/2；比例系数 s0由试验标定，其取值范围为[0，1]，取 0表示不考虑受压损伤对受拉刚度的影响，即原模型，取 1表示受压损伤对受拉刚度产生的影响程度最高.

图 1给出了修正混凝土单轴损伤本构模型的循环应力应变曲线，同时给出了原模型.可以看出修正模型考虑了受压损伤对受拉刚度的影响.

图1 修正Faria-Oliver单轴损伤模型循环应力应变曲线Fig.1 Cyclic stress-strain curves of uniaxial modified Faria-Oliver damage model

1.4 混凝土约束效应

采用密排箍筋来约束混凝土，可以显著提高混凝土的抗压强度与延性.假定约束混凝土损伤演化规律仍为式(3)，以参数A-、B-体现混凝土约束效应.采用式(8)计算约束混凝土受压强度与相应的应变[13]，即

式中：cmf为约束混凝土受压强度，cmε为相应的应变；c0f为无约束混凝土受压强度，c0ε为相应的应变；k为约束引起的提高系数[13].

1.5 损伤模型的初步验证

根据文献[14-15]的试验结果，采用了与原试验相同的混凝土材料参数，采用本模型分别计算得到了单调受拉(图2(a))、循环受压(图2(b))两种工况的应力应变曲线，同时给出了试验曲线做对比，从图 2中可看出，结果吻合较好，初步验证本模型的有效性.

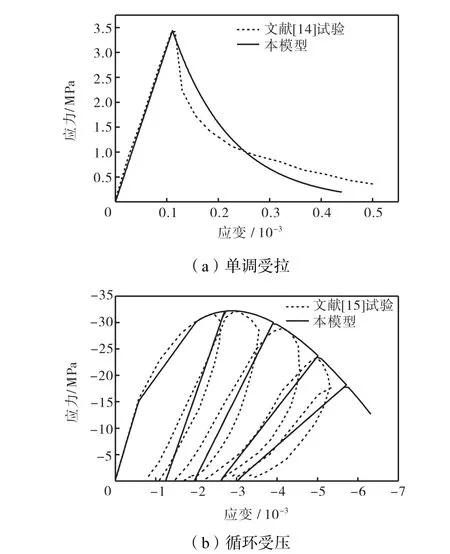
图2 计算与试验应力应变曲线对比Fig.2 Comparison between computational and experimental Fig.2 stress-strain curves

2 钢筋单轴本构模型

钢筋单轴本构模型采用修正 Menegotto-Pinto模型[5].Menegotto-Pinto模型的基本公式为

式中：(εr, σr) 为应变转折点；(ε0, σ0) 为弹性渐近线与屈服渐近线的交点；Eh为硬化模量；Es为弹性模量；εm为加载历史中应变的最大值或最小值(取决于当前应变的增减)；R0、a1、a2由试验确定.为了考虑等向硬化效应，Filippou等[5]对原模型做了修正，在屈服渐进线中引入了移动应力

式中：maxε为应变转折点处绝对值最大应变；yε、yσ分别为屈服应变与屈服应力；3a、4a等参数由试验确定.模型的循环应力应变曲线如图3所示.

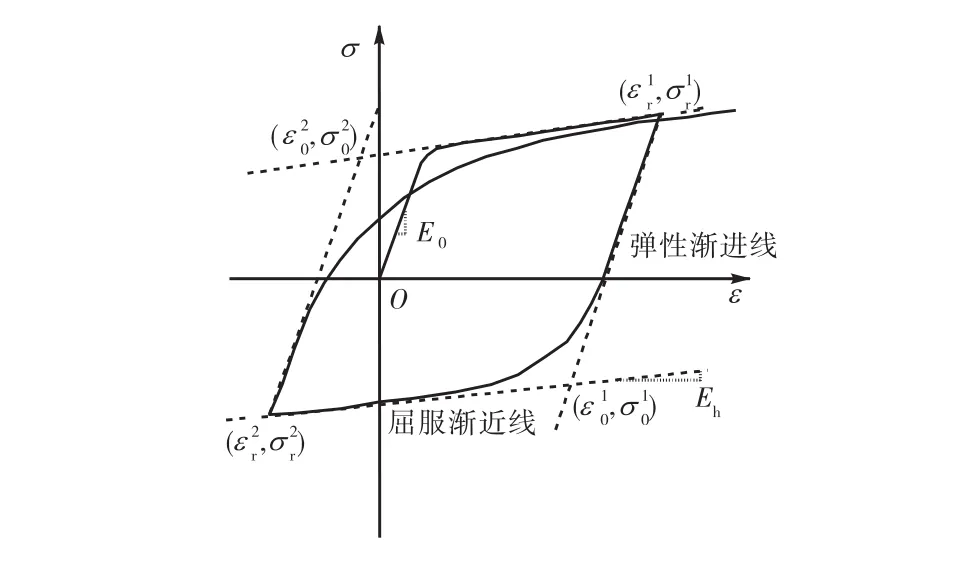
图3 Menegotto-Pinto模型循环应力应变曲线Fig.3 Cyclic stress-strain curves of Menegotto-Pinto model

3 ABAQUS用户子程序及纤维模型3 等效模拟

大型通用有限元软件 ABAQUS包含隐式(Standard)、显式(Explicit)两大模块，同时提供了分别适用于隐式与显式模块的用户材料子程序接口UMAT与 VUMAT，以满足用户的特殊需要.由于混凝土结构的地震响应及损伤过程的非线性程度很强，显式求解不存在收敛问题从而具有更好的适用性.在材料子程序接口 VUMAT中，需编程给出应力更新算法；同时在输入文件中，使用关键词“*USER MATERIAL”提供相应的材料模型参数值.本文对混凝土单轴修正Faria-Oliver损伤模型与钢筋单轴修正Menegotto-Pinto模型，利用 Fortran语言编制了相应的材料子程序VUMAT添加到ABAQUS中，以用于基于梁柱单元模型钢筋混凝土结构地震损伤分析.

对于梁柱单元，截面内力是由截面点的应力经数值积分而得到，常规纤维模型的截面积分方法实质为矩形法则；同时纤维模型对截面不同材料的分布能较方便地模拟.当前版本 ABAQUS提供的梁单元截面数值积分方法主要为梯形法则和辛普生法则，尚未提供纤维截面功能；研究表明可以通过相同类型梁单元叠加的等效模拟方法来实现截面配筋与考虑约束混凝土[9-10].即将钢筋、约束混凝土、无约束混凝土分为3个相同类型的梁单元，并且3个梁单元共用节点.由于梁单元类型相同，则单元形函数相同，3个梁单元共用节点，可以保证3个梁单元中任意点位移协调与平截面假定成立，从而实现纤维模型的等效模拟.

4 钢筋混凝土桥墩试件循环加载试验模拟

4.1 模拟模型

采用笔者建立的材料单轴模型及纤维模型等效模拟方法模拟 Kawashima等[16]所做的钢筋混凝土桥墩试件循环加载试验.试件尺寸及配筋如图 4(a)和图 5(a)所示，材料参数如表 1所示.在墩顶施加150,kN竖向压力，在距墩顶400,mm处侧向施加水平荷载，采用位移控制，加载时程曲线如图6所示.

图4 循环加载试验中的钢筋混凝土桥墩试件外形尺寸与有图4 限元模型Fig.4 Geometry and finite element model of RC bridge pier specimen for cyclic loading test

图5 循环加载试验中的钢筋混凝土桥墩试件截面尺寸及模拟模型Fig.5 Size and model of section of RC bridge pier specimen for cyclic loading test

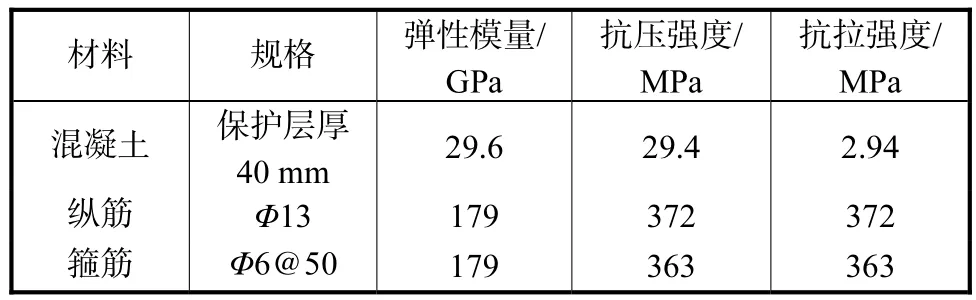
表1 钢筋混凝土桥墩试件材料参数Tab.1 Material properties of RC bridge pier specimen

图6 位移加载时程曲线Fig.6 Time history curve of displacement loading

钢筋混凝土桥墩试件有限元模型如图 4(b)所示，墩身用叠加的梁单元模拟，墩底固结.桥墩试件截面模拟模型如图 5(b)所示，约束混凝土采用矩形截面梁单元模拟，边长为320,mm；无约束混凝土采用箱形截面梁单元模拟，厚度为 40,mm；钢筋采用箱形截面梁单元模拟，厚度为 2.07,mm；以上梁单元均采用ABAQUS中的B31单元.约束混凝土与无约束混凝土采用单轴修正 Faria-Oliver损伤模型，其中0s取0.5；钢筋采用Menegotto-Pinto模型.

4.2 模拟结果及分析

数值模拟与试验得到的加载位置处水平位移与水平反力的滞回曲线分别如图 7(a)、(b)所示.从图7可看出模拟与试验所得的滞回曲线形状基本一致，但试验中最后一组循环加载的滞回曲线出现了一定的刚度、强度退化，模拟结果没有体现，原因可能是循环加载试验最后纵筋屈曲和粘结滑移所致，而本模型中钢筋采用的本构模型没有包含屈曲效应、纤维模型等效模拟方法未考虑混凝土与钢筋之间的粘结滑移.在本分析中，每根混凝土纤维损伤分布趋势相似，可大致反映桥墩试件的损伤发展与分布情况，典型纤维的最终受拉、受压损伤分布如图 8所示.图 8中直观地给出了混凝土纤维的最终受拉、受压损伤分布信息，显示了桥墩试件底部出现开裂、压碎损伤的实际情况.

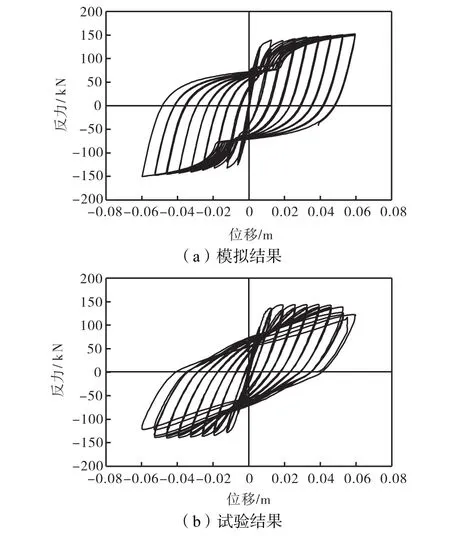
图7 加载位置处力-位移滞回曲线Fig.7 Force-displacement hysteretic curves at loading point

图8 混凝土纤维受拉、受压损伤分布Fig.8 Compressive and tensile damage contour plot of concrete fiber

5 钢筋混凝土桥墩试件振动台试验模拟

5.1 模拟模型

采用笔者建立的单轴材料模型及纤维模型等效模拟方法模拟 Nishida等[4]所做的混凝土桥墩试件振动台试验.试件尺寸及配筋如图 9(a)和图 10(a)所示，材料参数如表2所示，墩顶附加质量31 t.

钢筋混凝土桥墩试件有限元模型见图 9(b)，桥墩墩帽及墩顶附加质量用刚性梁单元模拟，墩身用叠加的梁单元模拟，墩底固结.桥墩试件截面模拟模型见图 10(b)，约束混凝土采用圆形截面梁单元模拟，直径为 520,mm；无约束混凝土采用环形截面梁单元模拟，厚度为40,mm；钢筋采用环形截面梁单元模拟，厚度为 1.92,mm；以上梁单元均采用 ABAQUS中的B31单元.约束混凝土与无约束混凝土采用修正Faria-Oliver单轴损伤模型，其中0s取 0.5；钢筋采用Menegotto-Pinto模型.采用瑞雷阻尼模型，阻尼比0.05.根据文献[4]采用Kobe波双向加载(x方向输入东西分量；y方向输入南北分量)，输入地震波幅值为原记录的80%，时间压缩为15,s.

图9 振动台试验时钢筋混凝土桥墩试件外形尺寸与有限元图9 模型Fig.9 Geometry and finite element model of RC bridge pier specimen for shaking table test

图10 振动台试验时钢筋混凝土桥墩试件截面尺寸及模拟模型Fig.10 Size and model of section of the RC bridge pier specimen for shaking table test

表2 振动台试验时钢筋混凝土桥墩试件材料参数Tab.2 Material properties of RC bridge pier specimen for Tab.2 shaking table test

5.2 模拟结果及分析

数值模拟与试验得到的墩顶附加质量质心处x、y方向位移时程曲线如图 11所示.由图 11可见，数值模拟得到的时程曲线虽与试验曲线有一定的差别，但基本趋势与试验曲线相符.在本分析中，钢筋混凝土桥墩截面不同混凝土纤维的损伤演化过程虽不完全一致但趋势相似，可大致反映整个桥墩损伤发展过程.本文中给出了典型混凝土纤维的受拉损伤演化图，如图12所示.纤维在0.85,s时底部出现受拉损伤，之后损伤快速发展直到1.5,s，之后受拉损伤发展较慢，直到15,s时损伤稍有发展.可发现此纤维在桥墩位移响应达到峰值前便发生较大损伤，之后纤维处裂纹只是在反复开闭，因此损伤发展变慢.分析表明，混凝土纤维受压损伤较小，其最终分布如图13所示.

图11 墩顶附加质量质心位移时程曲线Fig.11 Displacement time history curves at inertial center of Fig.11 added mass

图12 混凝土纤维受拉损伤演化Fig.12 Tensile damage contour plot of concrete fiber

图13 混凝土纤维受压损伤分布Fig.13 Compressive damage contour plot of concrete fiber

6 结 论

(1) 提出了混凝土单轴修正Faria-Oliver损伤模型并进行了修正以更好地描述混凝土单边效应，给出了单轴损伤模型的相关公式，并编制了相应的材料子程序，为以后基于纤维模型的钢筋混凝土桥梁结构地震损伤分析奠定了基础.

(2) 以大型有限元软件ABAQUS为平台，将混凝土单轴修正Faria-Oliver损伤模型及经典的修正Menegotto-Pinto钢筋模型编制为材料子程序VUMAT，采用纤维模型等效模拟方法，可以实现基于梁柱单元的钢筋混凝土桥梁结构地震响应及损伤分析.

(3) 将纤维模型或纤维模型等效模拟方法与混凝土单轴损伤模型结合，对钢筋混凝土桥梁结构进行地震损伤分析，不仅建模方便、计算效率高，而且提供了地震损伤演化过程信息，便于设计人员识别结构抗震薄弱部位，具有较强的工程实用性.

［1］司炳君，孙治国，艾庆华，等. 钢筋混凝土桥墩滞回性能的有限元参数敏感性分析及模型改进[J]. 工程力学，2009，26(1)：174-180.

Si Bingjun，Sun Zhiguo，Ai Qinghua，et al. Sensitive analysis and model modification for finite element analysis of R/C bridge piers under cyclic loading[J].Engineering Mechanics，2009，26(1)：174-180(in Chinese).

［2］Tsuchiya S，Maekawa K，Kawashima K. Three-dimensional cyclic behavior simulation of RC columns under combined flexural moment and torsion coupled with axial and shear forces[J].Journal of Advanced Concrete Technology，2007，5(3)：409-421.

［3］Casarotti C，Pinho R. Seismic response of continuous span bridges through fiber-based finite element analysis[J].Earthquake Engineering and Engineering Vibration，2006，5(1)：119-131.

［4］Nishida H，Unjoh S. Dynamic response characteristic of reinforced concrete column subjected to bilateral earthquake ground motions[C]//Proceedings of the13th World Conference on Earthquake Engineering. Vancouver，Canada，2004，Paper No. 576.

［5］Taucer F F，Spacone E，Filippou F C. A Fiber Beam-Column Element for Seismic Response Analysis of ReinForced Concrete Structures[R]. Berkeley：Earthquake Engineering Research Center，University of California，1991.

［6］黄宗明，陈 滔. 基于有限元柔度法和刚度法的非线性梁柱单元比较研究[J]. 工程力学，2003，20(5)：24-31.

Huang Zongming，Chen Tao. Comparison between flexibility-based stiffness-based nonlinear beam-column elements[J].Engineering Mechanics，2003，20(5)：24-31(in Chinese).

［7］张 强，周德源，伍永飞，等. 钢筋混凝土框架结构非线性分析纤维模型研究[J]. 结构工程师， 2008，24(1)：15-20.

Zhang Qiang，Zhou Deyuan，Wu Yongfei，et al. Study review of fiber model in nonlinear analysis of RC frame structures[J].Structural Engineers，2008，24(1)：15-20(in Chinese).

［8］Faria R，Oliver J，Cervera M. A strain-based plastic vis cous-damage model for massive concrete structures[J].International Journal of Solids and Structures，1997，35(14)：1533-1558.

［9］李承铭，李志山，王国俭. 混凝土梁柱构件基于截面纤维模型的弹塑性分析[J]. 建筑结构，2007，37(12)：33-35.

Li Chengming，Li Zhishan，Wang Guojian. Study on elastic-plastic finite element analysis based on section fiber beam-column elements[J].Building Structure，2007，37(12)：33-35(in Chinese).

［10］Susantha K A S，Ge H，Usami T. Cyclic analysis and capacity prediction of concrete-filled steel box columns[J].Earthquake Engineering and Structural Dynamics，2002，31(2)：195-216.

［11］Lee J，Fenves G L. A plastic-damage concrete model for earthquake analysis of dams[J].Earthquake Engineering and Structural Dynamics，1998，27(9)：937-956.

［12］Fremond M，Nedjar B. Damage in concrete：The unilateral phenomenon[J].Nuclear Engineering and Design，1995，156(1/2)：323-335.

［13］Farai R，Pouca N V，Delgado R. Seismic behavior of AR/C wall：Numerical simulation and experimental validation[J].Journal of Earthquake Engineering，2002，6(4)：473-498.

［14］Gopalaratnam V S，Shah S P. Softening response of plain concrete in direct tension[J].ACI Journal Proceedings，1985，82(3)：310-323.

［15］Sinha B P，Gerstle K H，Tulin L G. Stress-strain relations for concrete under cyclic loading[J].ACI Journal Proceedings，1964，61(2)：195-210.

［16］Nagaya K，Kawashima K. Effect of Aspect Ratio and Longitudinal Reinforcement Diameter on Seismic Performance of Reinforced Concrete Bridge Columns[R].Tokyo，Japan：Tokyo Institute of Technology，No. TIT/EERG 01，2001.

Seismic Damage Analysis of Reinforced Concrete Bridge Piers Based on Beam-Column Elements

LI Zheng1,2，LI Zhong-xian1,2
(1. School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. Key Laboratory of Coast Civil Structure Safety，Ministry of Education，Tianjin University，Tianjin 300072，China)

Faria-Oliver model is a simple and effective damage model for concrete. The uniaxial version of the Faria-Oliver damage model was proposed in the present paper. Meanwhile, the modification of Faria-Oliver model was introduced to describe the unilateral effect of concrete more properly. In addition, the material subroutines i.e. the modified Menegotto-Pinto model for reinforcing steel and the uniaxial modified Faria-Oliver model for concrete were implemented into VUMAT and the equivalent modeling strategy of fiber model was established within the FEA software ABAQUS. Furthermore, the numerical simulations of a cyclic loading test and a shaking table test of the reinforced concrete (RC) bridge piers were conducted. The results of the numerical simulations agreed well with the experimental ones. The present study indicates that the aforementioned uniaxial constitutive models and the equivalent modeling strategy of fiber model are effective and the seismic analysis of RC bridge piers using beam-column elements not only has a high computational efficiency but also provides information about seismic damage evolution.

reinforced concrete bridge pier；seismic damage；uniaxial damage constitutive model；beam-column element；fiber model

O346.5；TU352

A

0493-2137(2011)03-0189-07

2010-07-12；

2010-09-14.

国家自然科学基金资助项目(90715032，91015005，51021140003).

李 正（1981— ），男，博士研究生，zhenglitju@163.com.

李忠献，zxli@tju.edu.cn.