基于协商的Agent资源冲突消解算法研究
杨 萍,龙正平,王 桐
(第二炮兵工程学院,陕西 西安 710025)
分布式规划系统中Agent在制定计划时,由于各个Agent的局部视点,合并得到的整体计划往往存在冲突。Agent的计划冲突主要表现为时间冲突和资源冲突。时间冲突指局部计划合并为整体计划时,计划中的两个或几个子任务(或行动)间违反了时序关系。文献[1]对此进行了专门研究,这里不再讨论。本文主要针对计划合并中的资源冲突,研究不同资源冲突类型下的冲突消解算法。
在过去二十多年,研究者开发了多种冲突消解技术,包括协商[2~4]、仲裁[5]、竞选[6]、意图推理[7]等,以前的研究为 MAS冲突消解技术奠定了基础。但这些研究大多以通用性的冲突消解框架为重点,较少涉及具体的最优消解策略,特别是针对资源冲突这一具体背景的消解算法研究还比较少。
协商对多 Agent系统和分布式问题求解系统(DPS)来说是消解冲突,实现协作的最重要的方法之一,也是Agent交互中最普遍、最主要的表现形式[4]。本文运用协商理论建立资源冲突消解算法,并着重研究如何最优地制定协商策略,以提高协商效果。
1 资源冲突的分类
Agent在协作中使用的资源通常分为可重复利用的资源和消耗性资源,可重复利用资源实际中又可分为有限容量共享型资源,如信息、道路等,这些资源只能为有限用户共同使用,以及不可分享型资源(具有排它性),如设备、容量为1的阵地等;消耗性资源一旦被某个或某几个Agent占用,就不能再被其他Agent使用,如弹药等。消耗性资源的一个最大特点仍是容量受限。
分析各种资源冲突可以看出,有限共享型资源当资源容量为 1时转化为可重复利用的不可分享型情形,而容量大于1时与容量受限的消耗型资源发生冲突条件的最大区别在于占用资源的时间上的限制,其消解冲突的实质是一样的,因此对资源冲突消解问题的讨论可转化为对可重复利用的不可分享型资源以及容量受限的资源两种情形的研究。本文只对可重复利用的不可分享型资源的冲突消解问题进行研究。
2 可重复利用的不可分享型资源的冲突消解算法
对于不可分享型资源,其重要特点在于对一个固定时间区间只能有一个Agent拥有对该资源的使用权。文献[8]针对这类问题提出了一个“多轮”(multi-round)协商模型框架,并且从局部的视点上给出了一些协商策略,但还不够全面,本文从全局视点的角度探讨最优的协商策略,以更好地提高协商效果。
模型假设:
1)Agent间是合作的;
2)每个Agent均采用相同的出价策略,从而能保证结果度量值是一致和可比的;
3)Agent之间的通信是可靠的。
基于协商的不可分享型资源冲突消解算法思想是:每个冲突相关的Agent在接到协商消息后,发送一个占用该资源的时间区间、使用该资源的任务重要性效用和整个任务完成的时间消息;协商发起Agent根据收到的消息计算各Agent占用资源的综合效用,由此决定谁将获得资源的使用权。对于获得使用权的Agent将按照预定的方案使用该资源完成任务,其他的将不能按照原计划执行相关任务,他们将重新调度,然后开始新一轮的协商。具体的冲突消解算法为:
step1:每个Agent产生局部的计划方案,并传递局部计划;
step2:如果出现不可分享的资源冲突r,由发现冲突者Agenti发起协商,发送消息inform(i,j,u),j∈A,u∈S,其中A为参与协商的Agent集合,S为协商主题;
step3:每个收到消息的Agent计算自身占有该资源的任务重要性效用U1、该任务对资源占用的时间区间和整个任务完成时间etj,并发送协商消息 in form(j,i,u,vj1) ,u∈S,vj1∈V,其中V为Agent在协商过程中提交的协商意见,而vj1=U1∪∪et;
step4:协商发起者在规定时间内收到所有消息后,根据各协商意见,计算各个Agent对资源占用的综合效用,从中确定最佳的资源占有者,并发送accept(i,k,u,vks);对其他Agent发送reject(i,h,u);
step5:接到accept(i,k,u,vks)消息的Agent按原定计划执行任务,转step7;接到reject(i,h,u) 消息的Agent,转step6;
step6:对资源进行重新调度,转step1;
step7:监控任务执行过程,如果出现环境变化或意外情况,需要放弃该资源,则通知其他Agent;资源占用完成时,释放该任务资源。
下面讨论任务重要性效用和综合效用的计算方法。
1)任务重要性效用
任务的重要性应该包括两个方面:
一是任务的地位。比如,在机动作战中,既有具有真正机动作战目的的作战单元,也有配合其行动的佯动单元,显然两者任务的地位是不相同的。对任务地位的重要性可以通过一定的准则进行评估,也可以依据经验打分进行量化,这里不详细讨论评估细节,用一个反映任务地位的重要性权1表示。
二是对后续任务的影响。如果一个任务执行时间的延迟,对后续任务的影响很大,那么这个任务应该赋予更高的重要性权。评估对后续任务的影响也是一件比较复杂的事情,本文在这里将其简化,在大多数情况下,可以认为该任务后续的任务数量越多,该任务计划的变更产生的影响也越大。
设任务A后续任务的数量为n,对后续任务影响的重要性权为ω2A,0≤ω2A≤1,根据后续任务数量对重要性的影响特点,选用升半正态型曲线来刻画这种影响关系,定义
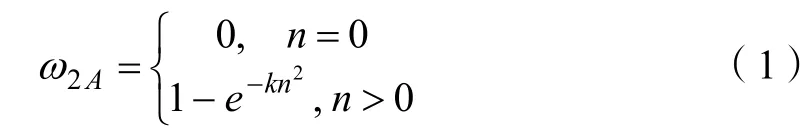
其中,k(>0)为调节参数。

于是,任务的重要性效用为λ,0 ≤λ≤1为权重。
除了任务的重要性因素,往往还需要考虑任务完成的时间因素。
2)任务时间效用
对于时间因素,这里主要考虑最重要的三个方面:任务完成时间、任务开始时间和任务持续时间。
通常情况下,我们当然希望通过协调资源使所有任务执行后的最晚完成时间尽量早。
考虑两个任务的情况,设要求A、B所在的整个任务最晚完成时间尽量早,并不是任何情况下任务A先开始就应该先执行,应该对两者综合考虑。设任务A、B的持续时间分别为durA、durB,任务B滞后于任务A,其开始时间差为t,任务A、B所在的整个任务完成时间分别为etA,etB,令

则有如下结论成立:
对使整个任务最晚完成时间尽量早问题,当t2−t1>t时(t<durA),应选B先执行;当t2−t1<t时,应选A先执行;当t2=t1,t>0时,越早开始的任务应先执行。如图1所示,
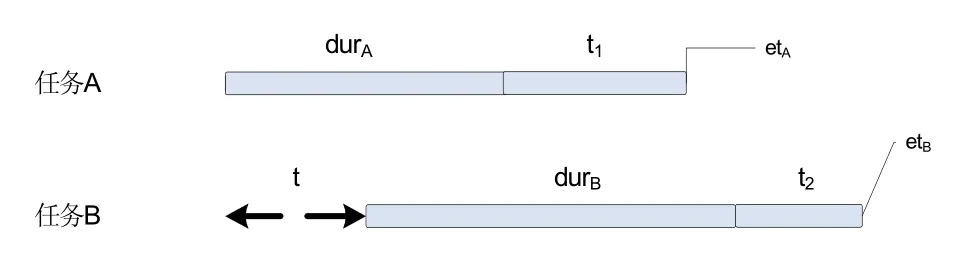
图1 任务A和任务B执行时间关系示意图
若A先执行时,A所在的任务链结束的时间为

B所在的任务链结束的时间为

而若B先执行,A所在的任务链结束的时间为
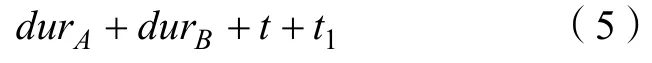
B所在的任务链结束的时间为

显然,式(3)的结束时间早于式(5),式(6)的结束时间早于式(4)(因为t<durtA);
而当式(4)大于式(5)时,即t1−t2>t时,有式(4)大于式(5)且式(4)大于式(6),故选B先执行;
而当式(3)小于式(5)时,即t1−t2>t时,有式(4)小于式(5)且式(3)小于式(5),故选A先执行;
当t2=t1,t>0时,越早开始的任务先执行可以节省资源等待时间,故A先执行。
由上证明可以保证在尽量提早所有任务的最晚完成时间的基础上,尽量减小资源等待浪费的时间。
如果t=0,t2=t1,在动态多变的环境中,任务的持续时间大小是应该考虑的。例如,任务A和任务B有相同的任务重要性效用、任务开始时间和后续任务执行时间,但任务A比任务B执行时间短,在下一轮的协商中,若新加入一个任务C,其重要性大于A、B,若A先执行,则重要任务C完成的时间要早于任务B先执行的情况。因此这种情况下,任务持续时间越短的任务越先执行。
综上,对任务A(其任务开始时间小于等于任务B),其任务时间效用可以定义为

3)综合效用
可以通过以下两种方式综合任务重要性和时间效用:
一是加权方式。这种方式对两方面因素综合考虑,综合效用计算式如下

其中 0 ≤α2,α1≤1,α2+α1=1。
二是优先方式。首先看任务重要性效用,如果相等,再根据时间效用进行选择,即

最终,资源占有权的选择原则:arg max{UA,UB}
如果参与资源竞争的不只两个任务,则首先任选两个任务依据上述原则进行选择,每次具有资源拥有权的任务再与剩余任务中的一个进行竞争选择,直到所有任务进行完毕。
3 算 例
在分布式作战仿真系统中,设Agenti、j、k分别制定了各自的局部计划如图2(a)、图2(b)、图2(c)所示。
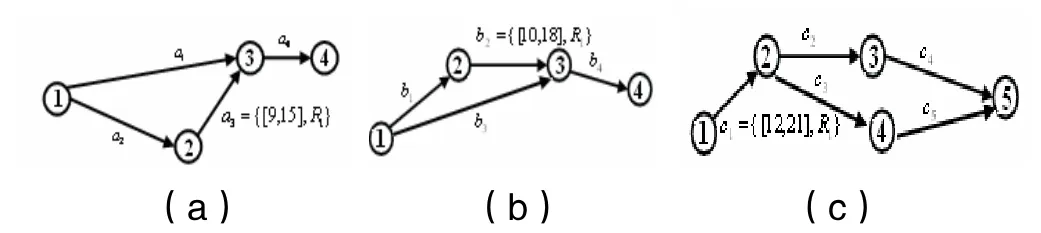
图2 局部计划图
在将局部计划合并为整体计划中,执行任务a3、b2、c1时出现了占用不可分享型资源R1的冲突。
① A genti首先检测到该冲突,因此发起协商,发送消息 in form(i,j,u), in form(i,k,u),u= {R1};
② 接到消息的Agentj、k分别计算自身占有该资源的任务重要性效用U1、该任务对资源占用的时间区间 [stR1,etR1]和整个任务完成时间et,并发送消息inform(h,i,u,vh1),h= {j,k},其中vj1=0.8∪[10,18]∪34,vk1=0.85∪[12,21]∪45;
③ A genti接到消息后计算每个的综合效用。设Agenti的任务重要性效用U1、对资源占用的时间区间[stR1,etR1]和整个任务完成时间et为:0.7 5∪[9,15]∪37,首先考虑a3与b2,根据式(7),易得U2a3=1,U2b2=0;利用式(8)计算综合效用,得

故应先选择Agenti占用资源R1去执行任务a3。类似地再在a3与c1中进行选择,最终得到:Ua3=0.525,Uc1=0.895,故在这一轮的协商中,选择Agentk先执行任务c1。
Agenti发送消息accept(i,k,u,vks),对Agentj发送reject(i,j,u);
④ A gentk按原计划执行任务,Agenti与Agentj需要重新调度。
4 结束语
本文研究了计划合并中的资源冲突消解问题,运用Agent协商理论,提出了可重复利用的不可分享型资源的冲突消解算法,论证了最优的协商策略,较好地解决了Agent分布式规划中出现的一类资源冲突问题。算例表明,论文给出的冲突消解算法具有可操作性。
[1]徐瑞.基于多智能体的深空探测器自主任务规划方法与系统仿真[D].哈尔滨:哈尔滨工业大学,2004.
[2]徐润萍,王树宗,顾健.兵力协同计划资源冲突协商方法研究[J].系统仿真学报,2005,17(5): 1216-1220.
[3]G.Zlotkin,J.S.Rosenschein.cooperation and conflict resolution via negotiation among autonomous agent in Non-cooperative domains[J].IEEE SMC,1991,21(6):1317-1324.
[4]N.R.Jennings,S.Parsons,C.Sierra.Automated negotiation[C].In: Proceedings of the 5th International Conference on the Practical Application of Intelligent Agents and Multi-Agent System (PAAM-2000).Manchester,UK.2000: 23-30.
[5]R.Steeb.Architectures for distributed intelligence for air fleet control[R],Rand Corp.,Santa Monica,CA,Tech.Rep.R-2728-ARPA,1981.
[6]E.Ephrati and J.S.Rosenschein.Multi-agents planningASa dynamic search for social consensus[C].In:Proceedings Thirteenth International Joint Conference Artificial Intelligence.Morgan Kaufmann,1993:423-429.
[7]H.Sugie.Placing objects with multiple mobile robotsmutual help using intention inference[C].In: Proceedings IEEE International Conference on Robotics Automation.IEEE,1995: 2181-2186.
[8]Keith Decker, Jinjiang Li.Coordinating Mutually Exclusive Resources using GPGP[J].Autonomous Agents and Multi-Agent Systems,2000(3):133-157.

