基于模糊层次分析法的战役情报效能评估
余 力,岳振军
(解放军理工大学,江苏 南京 211101)
军事情报是对获取的军事斗争所需求的情况进行分析判断的成果,是筹划和指导战争及指挥作战的重要依据[1]。正确的军事行动有赖于正确的决策,而正确的决策来源于准确及时的情报。准确及时的情报可以减少敌情和作战环境的不确定性,降低决策风险,帮助指挥员作出最优决策。
战役情报是指组织实施战役所需的情报,是战役指挥员了解战区环境、判断敌情、定下决心、把握战场态势、组织各种支援的保障条件。一般来说,战役情报包括作战区域内敌军的兵力、编成、番号、部署、装备、战斗力、行动企图、指挥官特点、后勤补给以及作战地形、气象(水文)等方面的情况[1]。
战役情报的效能是某一份情报或某一情报集对于特定战役的支持力度,即对作战进程和结局产生有利作用的程度以及满足预期军事任务目标的程度度量。战役情报的效能是通过战役这一军事活动体系而提出来的,表现为保障和支持某些军事活动的效能指标。对包括战役情报在内的军事情报进行客观准确的效能评估,有助于增强情报工作的针对性,优化情报工作流程和资源配置,调动情报人员的积极性和主观能动性,更有助于辅助决策,使指挥员的各类决策趋于科学化、合理化,最终提高军事行动效能。
1 战役情报效能评估指标体系的建立
1.1 评估指标体系的建立
根据战役情报在战役中的作用,收集整理相关资料及专家咨询,拟定战役情报效能评估指标体系如图1所示。

图1 战役情报效能评估指标体系
1.2 指标体系的权重计算
1.2.1 权重计算
在确定各指标相对权重时主要采用专家打分法,立足于军事情报专家及军事指挥员对各准则的自我理解之上,因此,客观上必然存在一定的误差。为了较为客观准确地得出调查的结论,找出调查数据的规律,采用集中趋势的有关原理进行统计分析[2]。现以一级指标层的数值统计进行众值计算的简单介绍,根据专家打分结果,获知战场态势以辅助决策判断的效能A1相对于提供系统资料以保障作战需要的效能A2的重要性δA1,A2的数据统计表如表1所示。

表1 A1相对于A2的重要性δA1,A2的数据统计表
从表1可以看出,打1分的有3人,打2分的有5人,打3分的有5人,其余分值的数量较小。打1~3分的人数为13个,占专家总数的86.7%,表明大多数专家的意见趋于一致,根据众值的确定原则,认为该组数据的众值在1~3之间,那么A1相对于A2的重要性,即
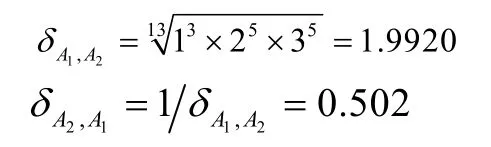
同理可依次得出,δA1,A3,δA3,A1,δA2,A3,δA3,A2,并且有,由此,可得出一级指标层的判断矩阵。
1.2.2 指标权重的确定
确定下一层次因素对上一层次因素的权重分配,构成因素权重集W:
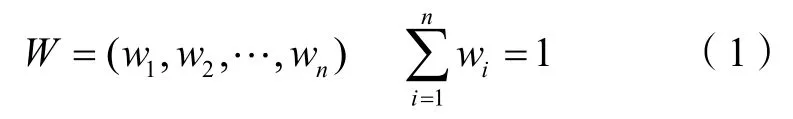
根据权重计算结果得出的一系列判断矩阵,可以采用层次分析法(AHP)来确定各层指标的权重,具体计算方法见文献[3]。
2 战役情报效能模糊综合评价
所谓模糊综合评价就是以模糊数学理论为基础,应用模糊关系合成的原理,将一些边界不清不容易定量的因素定量化,进行综合评价的一种方法[4]。它通过构造等级模糊子集把反应被评价事物的模糊指标进行量化(即确定隶属度),然后利用模糊变换原理对各指标综合。一般情况下,按以下基本程序进行。
2.1 确定评价对象的多层结构评估指标集:
如图1所示,评价对象的指标集为A={A1,A2,… ,AN1}。其中,N1表示第一级指标个数;Ai= {Ai1,Ai2,… ,AiN2},其中,N2表示第i个一级指标下的二级指标个数。
2.2 确定评语等级论域:
因为所建立的指标不能用准确的数学表达式来表达,所以在此运用专家的评语来表述指标值。评语等级集合可表示为V= {V1,V2,… ,Vp},p是评语的等级数,每一个等级可对应一个模糊子集。一般地,评价等级数p取[3,7]中的整数。若p过大,则语言难以描述且不容易判断等级归属;若p过小,则会造成评价的准确性不高。在此,根据战役情报特点,评语等级论域取V={特别重要,重要,比较重要,一般重要,不重要}。
2.3 进行单因素评价,建立模糊关系评估矩阵。

这里,rjk表示单独考虑第i个因素中的第j个子因素对第k个评语等级的隶属度。

这里,rik表示单独考虑第i个因素对第k个评语等级的隶属度。
隶属度的求法有等级比重法、隶属函数法、频率法、专家评判法等。在这里采用专家评判法,即邀请多位专家对某特定战役情报的效能依据评价集的p个等级进行评定,将结果填入相关专家评审表,最后计算出各指标的模糊评价集为:,其中,r1~rp依次为该指标对于指标集第1项至第p项的相对频率(即隶属度)。
2.4 模糊层次运算
利用合适的合成算子将权向量 W 与合成得到战役情报效能的模糊综合评价结果向量。

其中,“◦”为模糊矩阵合成算子,针对不同形式,对应不同的使用范围。一般选用四种算子:主因素决定型(M∧∨,),主因素突出型(M∨·,),不均衡平均型M(∧,⊕)和加权平均型M(·,⊕)。加权平均型对所有因素依权重大小均衡兼顾,针对情报效能评估的特点,不妨采用加权平均型算子(M⊕·,),即

式中,bj(j=1 ,2,… ,p)表示战役情报的综合效能从整体上看对Vj等级模糊子集的隶属程度。
对于多个层次的评估,采用从低层到高层逐层计算的方法即可求出最终评价结果。
2.5 对模糊综合评价结果向量进行分析
模糊综合评价的结果是被评对象对各等级模糊子集的隶属度,表现为一个模糊向量,而不是一个点值,因而它能提供的信息比其他方法更丰富。然而,若对多个对象进行比较排序,就需要进一步处理模糊综合评价结果向量。对模糊评价结果的分析常用的方法有最大隶属度原则、最大接近度原则、加权平均原则、模糊向量单值化等。
3 应用实例
3.1 确立各指标的权重集
结合众值计算方法和层次分析法,得出一级指标层相对于目标层的权重集W=(w1,w2,w3),即wi(i= 1 ,2,3)表示A1,A2,A3对A的权重。同理得出,二级指标层相对于一级指标层的权重集:

wij表示指标Aij对准则Ai的权重。
例如评估某个战役情报集的综合效能,根据某专家组的打分情况,并按照以上方法,得出下列权重集:W= ( 0.45,0.30,0.25),W1= ( 0.26,0.21,0.25,0.28),W2= ( 0.33,0.34,0.33),W3= ( 0.40,0.30,0.30)。
3.2 建立单指标评判矩阵
对专家打分结果采用模糊统计方法来确定各个指标属于不同评判等级的程度,并构成相应的模糊评判矩阵。令(其中N为专家人数,xijp为因素Aij被评为vp的次数),详见表2。

表2 二级指标的统计
根据多层次模糊综合评价模型,对战役情报效能评估体系各层由下向上逐层进行计算。
如 A1的单级评价值矩阵1,采用常规矩阵乘规则,有:


3.3 求得战役情报效能评估结果

由此可见,该专家组认为此战役情报集特别重要的程度为0.4499,认为重要的程度为0.3131,认为比较重要的程度为 0.1582,认为一般重要的程度为0.0613,认为不重要的程度为 0.0175。根据最大隶属度原则,认为该战役情报集对战役目的的实现作用特别重要。
4 结束语
模糊层次分析法具有较高的科学性和客观性,计算方法简单、使用方便。因而运用模糊层次分析法对战役情报效能进行评估是一种可行的方法,对于衡量某特定情报集在战役中的支持力度具有一定的参考价值。然而,提出的评估指标体系还需在实践中不断地调整和完善,确保评估结果的科学性和有效性。
[1]闫晋中.军事情报学[M].北京:时事出版社,2003.
[2]杨国良.统计学原理[M].重庆:重庆大学出版社,2006.
[3]许树柏.层次分析法原理[M].天津:天津大学出版社,1988.
[4]叶义成,柯丽华,黄德育.系统综合评价技术及其应用[M].北京:冶金工业出版社,2006.
[5]马茂冬,韩尧,张倩.基于模糊层次分析法的应急能力评估方法探讨[J].中国安全生产科学技术,2009,5(2):98-102.

