基于改进Apriori算法的考试成绩分析

李 翔，张 伟

(1.江南大学 物联网工程学院，江苏无锡214122;2.淮阴工学院计算机工程学院，江苏淮安223003)

0 引言

Apriori算法［1－2］是由 Agrawal、Imielinski、Swami等人共同提出的关联规则数据挖掘算法。Apriori算法是一种基于水平数据表示、广度优先搜索的数据挖掘算法。本文通过对学生成绩的分析，对Apriori算法进行深入研究，在此基础之上提出一种在垂直数据表示的数据集上采用交叉计数执行广度优先搜索的新算法。新算法结合了垂直数据表示和交叉计数高效率的优势以及Apriori算法的剪枝策略，以降低计数候选集数目。通过对学生多门课程成绩的仿真分析，能快速发现相关课程之间的成绩影响关系，为学校教学和学生学习提供参考。

1 理论基础

1.1 关联规则

定义1:设I={i1，i2，...，im}是数据项集合;设与任务相关的数据D是数据库事务中的集合，其中每一个事务T是一组项的集合，使得T⊆I;每一个事务都包含一个唯一的标识符T⊆D。设A为一个数据项集合，当且仅当A⊆T时称事务T包含A［3－4］。一条关联规则就是一个形如A⇒B的蕴涵式，其中 A⊆I，B⊆I，且 A∩B=Φ。

关联规则AB成立的条件为:

(1)具有支持度S%，S%=support(A⇒B)=P(A∪B)，即数据库D中至少有S%的记录包含A∪B。

(2)具有可信度C%，C%=confidence(A⊆B)=P(B|A)=P(A∪B)/P(A)，即数据库D中包含了A记录的同时包含B至少为C%。

支持度是数据项在数据库中所占的比例，可信度是该规则的强度。满足最小支持度min_sup的项目集合称为频繁项集;既满足最小支持度min_sup也满足可信度min_conf阈值的规则称为强关联规则，通常记作A⇒B(S%，C%)。

1.2 Apriori算法

Apriori算法是挖掘产生布尔关联规则所需频繁项集的基本算法。Apriori算法完成频繁项集的挖掘工作主要是利用了一个层次顺序搜索的循环方法来实现。该循环方法就是利用k－项集来产生(k+1)－项集。详细步骤是:首先找出频繁1－项集，称为L1;再利用L1来挖掘L2，即频繁2－项集;不断这样循环下去直到无法发现更多的频繁k－项集为止。每挖掘一层Lk就需要遍历整个数据库一遍。

Apriori算法具体描述如下:

输入:事务数据库D，最小支持记数阈值min_sup

输出:D中的频繁项集L

步骤:

函数apriori_gen

输入:Lk－1频繁(k－1)－ 项集

输出:候选集Ck

步骤:

2 改进的Apriori算法

经过研究发现，Apriori算法具有两个重要性质。

(1)当判断k维候选项集R的(k－1)维子集是否包含在Lk－1的过程中，无需判断所有的k个(k－1)维子集。因为连接成候选项集R的两个子集{R［l］|0≤l≤k －2}和{R［l］|0≤l≤k －1，l≠k－2}在Lk－1中，所以只要判断其他k － 2个子集就可以了。

(2)每个事务T及事务中的项目集如果按字典顺序排序，对于两个(k－1)维频繁项集Ix和Iy，只要Ix和Iy不能连接，则Ix与Iy之后的所有项目集都不满足连接条件，可以不必测试连接判断。

综合应用以上两个重要特性，可以提出的改进的Apriori算法以垂直数据集表示方式上的执行广度优先搜索和交叉计数的改进算法。通过对项集和项集中的项按照字典顺序保存，即先挖掘出所有的频繁k－项集并记录下来，然后对前k－1个项相同的项集连接成一个候选k+1项集，连接的时候采用上述重要性质2从而减少判断的次数;对候选项集采用上述重要性质1进行剪枝判断，如果候选项集不符合Apriori性质，就剪掉，如果符合则采用交叉计数的方式直接计算出支持度。

∥采用广度优先搜索

//采用 Link Item()函数来判别 Xi，Xj是否可以连接生成一个候选(k+1)维项集。只要其前k－1个项完全相同，前者的第k个项小于后者，就可以连接生成一个(k+1)维候选项集。具体函数如下:

//采用Trimed()函数来判别k维项集R的k个(k－1)维子集是否都在Lk－1中，如果有某个(k－1)维子集不在Lk－1中，那么该候选项集R一定是非频繁的，则返回true。将计算次数由k减少到k－2，具体函数如下:

3 算法性能分析

实验硬件环境为 Intel Core2 Duo T7350，3G DDR3内存，软件环境是 Visual C++6.0，实验数据集采用T10 I4D100k，来源Frequent ItemsetMining Imp lementations Repository(http://fimi.cs.helsinki.fidata)。两种算法所用计算时间如图1所示。

从图1可以看出改进后的Apriori算法比原来算法运行时间减少，而且随着最小支持度的降低和需要挖掘的频繁项集数增多，改进后的Apriori算法运行优势更明显。

图1 不同最小支持度下两种算法运行时间比较图

4 算法应用

将改进的Apriori算法应用于学生成绩分析，实验时采集了学校教务系统中学生考试的多门成绩作为实验数据。随机抽取某一届学生的如下几门课程:C++程序设计，C#程序设计，JAVA程序设计，成绩发布见表1所示。

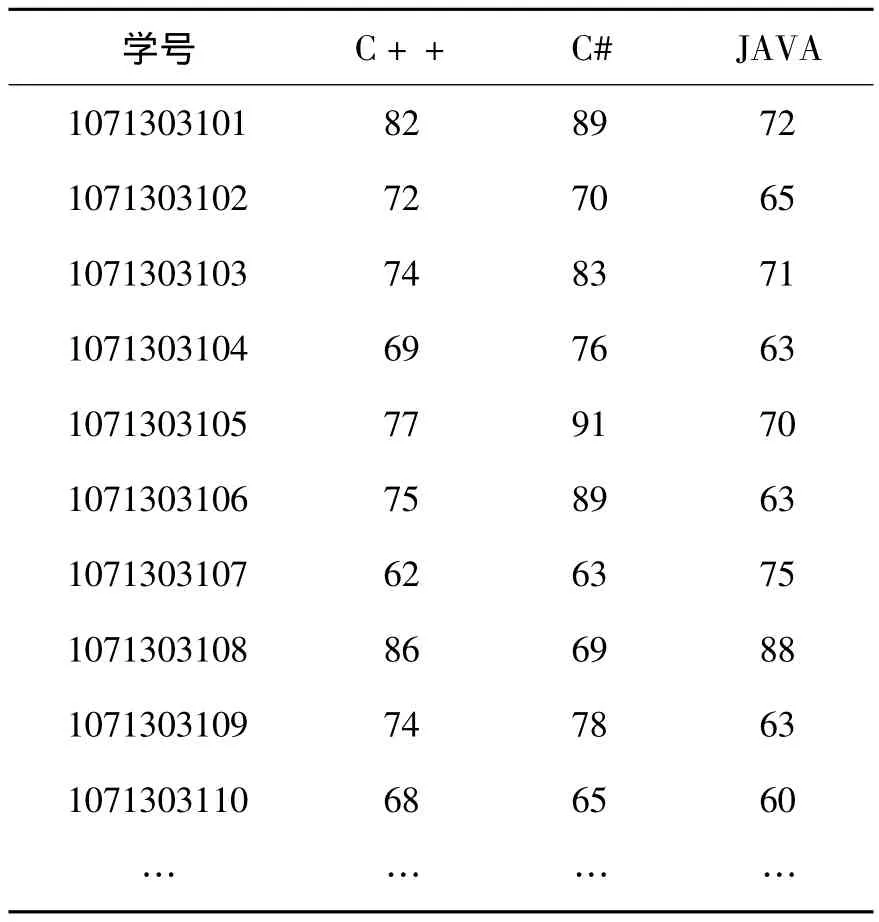
表1 学生考试成绩数据表

实验中对学生成绩进行关联分析挖掘时需要的是逻辑型数据，所以将表1的数据转换为布尔型。由于需要挖掘的是几门课之间的良好关系，所以75分以上字段设为“TRUE”，表示事务中存在该项，其他设为“FALSE”，表示事务中不存在该项。将表1转化为关联规则算法便于处理的样式，见表2所示。

表2 学生成绩分析数据表

要对表2中的良好课程进行关联规则挖掘，本次实验设定最小支持度为20%、置信度为50%。将表2中180条记录作为Apriori关联规则挖掘的数据，运用Apriori改进算法后，得到表3所示的实验结果。

表3 频繁项集表

由表3计算出最终频繁项集中非空子集的置信度，并删除小于最小置信度阈值的记录，最终产生关联规则如下:

(1)C++C#，confidence=62/72 86.11%;

(2)C#C++ ，confidence=62/95 65.26%;

(3)JAVAC#，confidence=35/40 87.50% 。

从以上运行结果得出以下潜在的关联:

(1)C++程序设计良好时，C#程序设计有86.11%的良好可能;

(2)C#程序设计良好时，JAVA程序设计有65.26%的良好可能;

(3)JAVA程序设计良好时，C#程序设计有87.50%的良好可能。

5 结论

本文针对关联规则挖掘算法中提高挖掘频繁项集效率问题，提出了一种改进的Apriori算法。并将该算法应用于试卷成绩分析中，实验结果给出了学生各科目试卷成绩的优良影响关系，为学校指导学生的学习及今后的工作提供了决策支持。

［1］Agrawal R，Imielinski T，Swami A.Mining association rules between sets of item s in large databases［C］//Proc of ACM SIGMOD Conference on Management of Data，ACM New York，NY，USA，1993:207－216.

［2］Agrawal R，Srikant R.Fast algorithm form ining association rules in large databases［C］//Proceedings of the 20 th International Conference on Very Large Data Bases，Morgan Kaufmann Publishers Inc San Francisco，CA，USA，1994:487－499.

［3］王月行，马垣，胡志宇.基于概念格的关联规则挖掘方法［J］.计算机工程与设计，2009，30(22):5062 －5064.

［4］陈耿，朱玉全，杨鹤标.关联规则挖掘中若干关键技术的研究［J］.计算机研究与发展，2005，42(10):1785－1789.

［5］徐章艳，刘美玲.Apriori算法的三种优化方法［J］.计算机工程与应用，2004，40(36):190－193.

［6］陆建江，张文献.关联规则挖掘的基本算法［J］.计算机工程，2004，30(15):34 －35.