不完备序值系统中的粗糙集与模糊粗糙集
杨习贝,於东军,窦慧莉
(1.南京理工大学 计算机科学与技术学院,南京210094;2.江苏科技大学 计算机科学与工程学院,江苏镇江212003)
0 引言
近年来,随着实际工程应用的需要,使用粗糙集理论[1-2](Rough Set Theory,简称 RST)从不完备信息系统[3-7](Incomplete Information System,简称IIS)中获取知识已成为一个热点研究问题。由于数据填充或删除处理IIS中的未知属性值(间接处理方法)会影响到原有的数据分布情况,使得挖掘出来的规则具有较大的不确定性,因此将传统RST中的不可分辨关系(等价关系)拓展为其他较弱的二元关系,从而使用各种拓展的粗集模型处理IIS(直接处理方法)正受到越来越多的学者的关注。
一般来说,IIS中的未知属性值可能具有两种不同的解释。首先,所有的未知属性值仅仅是被遗漏的,但又是确实存在的,根据这样的解释,Kryszkiewicz构建了满足自反和对称性的容差关系,并研究了IIS中的知识约简问题。另一方面,所有的未知属性值被认为是丢失的,是不允许被比较的,据此,Stefanowski等人构建了非对称相似关系并建立了近似集的概念。
另一方面,值得注意的是经典粗糙集理论是建立在等价关系的基础上的,它并未考虑信息系统中属性值之间的顺序关系,为了解决这个问题,Greco提出了基于优势关系的粗糙集模型[8-11]。在优势关系粗糙集模型中,分类是建立在优势关系的基础上的,并且被近似的集合不再是单纯的等价类,而是等价类的上并集和下并集。
Shao首先研究了不完备序值信息系统中的粗糙数据分析问题,在他的不完备序值信息系统中,所有的未知属性值被认为是遗漏的,并且属性值之间存在序关系,根据这种语义解释,Shao提出了一种扩展优势关系及相关的粗糙集模型。在Shao的工作基础上,Luo[12]提出了限制优势关系粗糙集模型,并与Shao的扩展优势关系粗糙集进行了对比分析,结果表明Luo的限制优势粗糙集模型具有更高的近似精度。
在本文中,笔者主要考虑的是具有丢失型未知属性值的不完备序值信息系统,由于此时所有的未知属性值都是丢失的,与其他属性值是不可以比较的,扩展优势关系和限制优势关系都不再适用;同时,因为不完备序值信息系统中的属性值之间存在序关系,因而Stefanowski的非对称相似关系也不再适用。为了解决这个问题,笔者提出了相似优势关系的概念,相似优势关系是不完备信息系统中非对称相似关系与序值信息系统中优势关系两者的一种广义化表现形式。
本文的主要内容安排如下:第一节简要介绍了不完备决策系统,第二节定义了不完备序值决策系统,提出了相似优势关系,并给出了基于相似优势关系的粗糙集模型,第三节在不完备模糊序值决策系统中给出了基于相似优势关系的模糊粗糙集模型,第四节总结全文。
1 不完备决策系统
一个不完备决策系统为一个四元组:IDS=<U,AT∪D,V,f>。其中U是一个被称为论域的非空有限的对象集合;AT是非空有限条件属性集合,D是非空有限的决策属性集合且AT∩D=Ø;VAT是条件属性的值域(可包丢失型空值,文中用“?”表示),VD是决策属性的值域集合并且“?”∈VD,V=VAT∪VD;f为信息函数,对于∀a⊆AT,∀x∈U,有 f(x,a)∈ Va。
“?”表示对象在某个属性上的取值是不存在的,因此不能和其他任何已知属性进行比较。根据这样的解释,可定义如下所示的二元关系。
定义1 在不完备决策系统IDS中,对于∀A⊆AT,由A决定的相似关系记为SIM(A)且
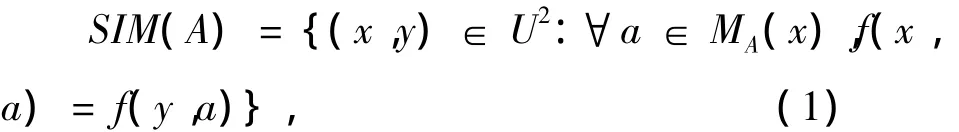
其中MA(x)={∀a∈A:f(x,a)≠?}。
很明显,定义1中所示的相似关系满足自反性和传递性,但并不一定是对称的,因此称之为非对称相似关系。接着,Stefanowski给出了非对称相似于x的集合SA(x)={y∈U:(y,x)∈SIM(A)},x与之非对称相似的集合S-1A(x)={y∈U:(x,y)∈SIM(A)}。
定理1 在不完备决策系统IDS中,对于∀A∈ AT,有

定义2 在不完备决策系统IDS中,有A⊆AT,U/IND(D)={D1,D2,…,Dm}表示根据决策属性集合D所构成论域上的划分,则对于∀Di∈U/IND(D)(1≤i≤m),决策类的Di下、上近似集记为 A*(Di),A*(Di)且

定理2 设IDS为一不完备决策系统,A⊆AT,对于 ∀Di∈ U/IND(D),有
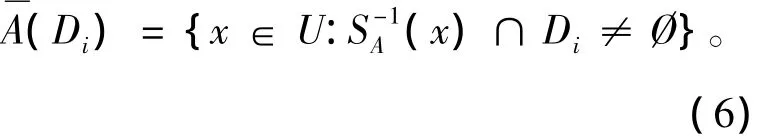
证明:只需证∪{SA(y):y∈Di}={x∈U:。对于∀x∈U,若≠Ø,则必定存在 y∈ Di且,即 x∈SA(y),所以 x∈∪ {SA(y):y∈ Di},即{x∈ U:⊆∪{S(y):y∈D}。对于∀xAi∈∪{SA(y):y∈Di},必定存在y∈Di并且x∈SA(y),因此成立,即证毕。
2 不完备序值决策系统
一个不完备序值决策系统是四元组IODS= < U,AT∪D,V,f>,AT为序条件属性集合,D为序决策属性集合,VAT和VD集合都是全序集,其中VAT中可能包含丢失型未知属性值“?”且“?”∉VD。当不完备序值决策系统中只有序条件属性集合存在时,称之为不完备序值信息系统(Incomplete Ordered Information System,简称 IOIS)。
定义3 在不完备序值信息系统IODS=<U,AT∪D,V,f> 中,对于∀A⊆AT,由A决定的相似优势关系有以下两种表现形式:
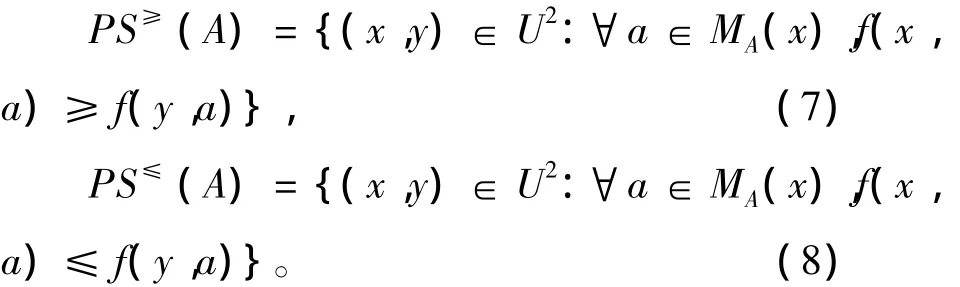
很明显,相似优势关系仅满足自反性和传递性,但是不一定满足对称性。为描述方便起见,对于∀x∈U,记,对于,有x相似于y且x优于y,,对于,有y相似于x且y优于x,,对于,有x相似于y且x劣于y,对于),有y相似于x且y劣于x。
在IODS中,由于所有对象的决策属性值都是已知的,因而决策属性集合D构成了论域上的划分CL={CLt:t∈ T},其中 T=1,2,…,n。对于 ∀r,s∈T,若r>s,则认为CLr中的对象要优于CLs中的对象。令1,…,n,x∈CL≥t表示x至少属于决策类CLt,x∈CL≤t表示x至多属于决策类CLt。
定义4 在不完备序值决策系统IODS中,若有 A⊆AT,则对于∀CL≥t(1≤t≤n),CL≥t的下近似、上近似定义为
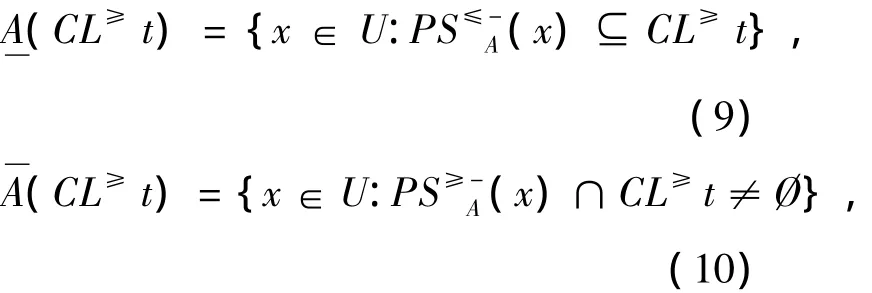
对于∀CL≤t(1≤t≤n),CL≤t的下近似、上近似定义为

定理3 在不完备序值决策系统IODS中,有A⊆ AT,对于 ∀CL≥t,CL≥t,就有
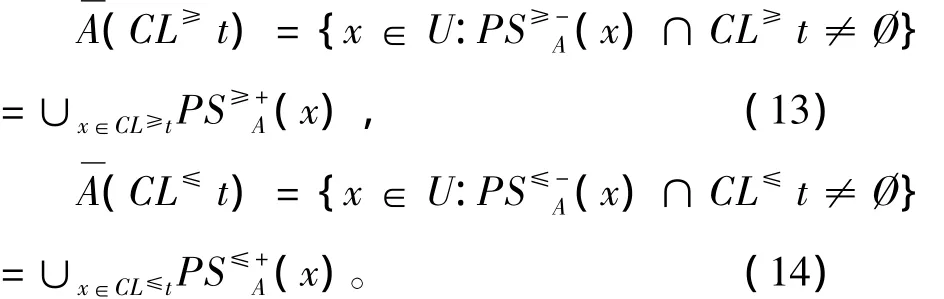
证明:类似于定理2的证明过程。
定理4 在不完备序值决策系统IODS中,若A⊆ AT,则
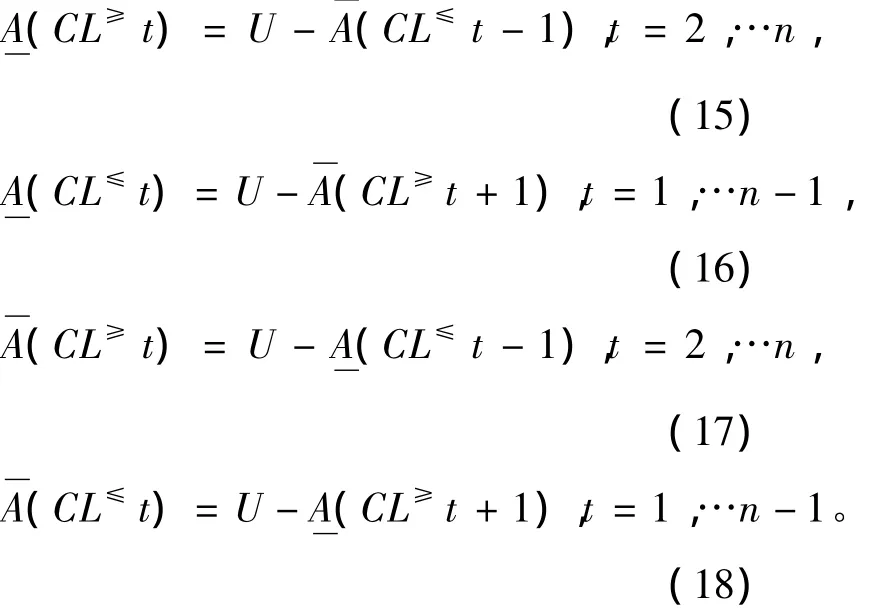
3 不完备模糊序值决策系统
一个不完备模糊序值决策系统是一个不完备序值决策系统IODS= <U,AT∪D,V,f>,其中对于∀a∈AT∪D,∀x∈U,有f(x,a)∈[0,1]。为简便起见,本文所讨论的不完备模糊序值决策系统中仅含有一个决策属性,即d。
在不完备模糊序值决策系统中,由于属性的表现形式是模糊的,因而被近似的概念不再是一个清晰的集合,而是一个模糊集合。此时可以采用模糊粗糙集的方法构建近似集。
定义5 在不完备模糊序值决策系统IODS中,若有A⊆AT,d的下、上近似集分别记为和,他们的模糊粗糙隶属度分别为
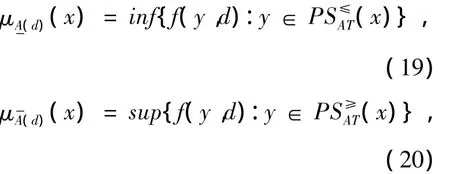
定理5 在不完备模糊序值决策系统IODS,若 A⊆ AT,则
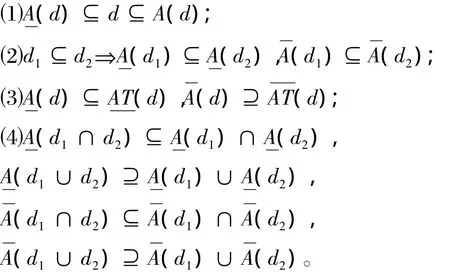
⑵因为 d1⊆ d2,所以对于任意的 y∈,有 f(y,d1)≤ f(y,d2)。根据定义 5 就有μA(d1)(x)≤μA(d2)(x),即。类似地,易证
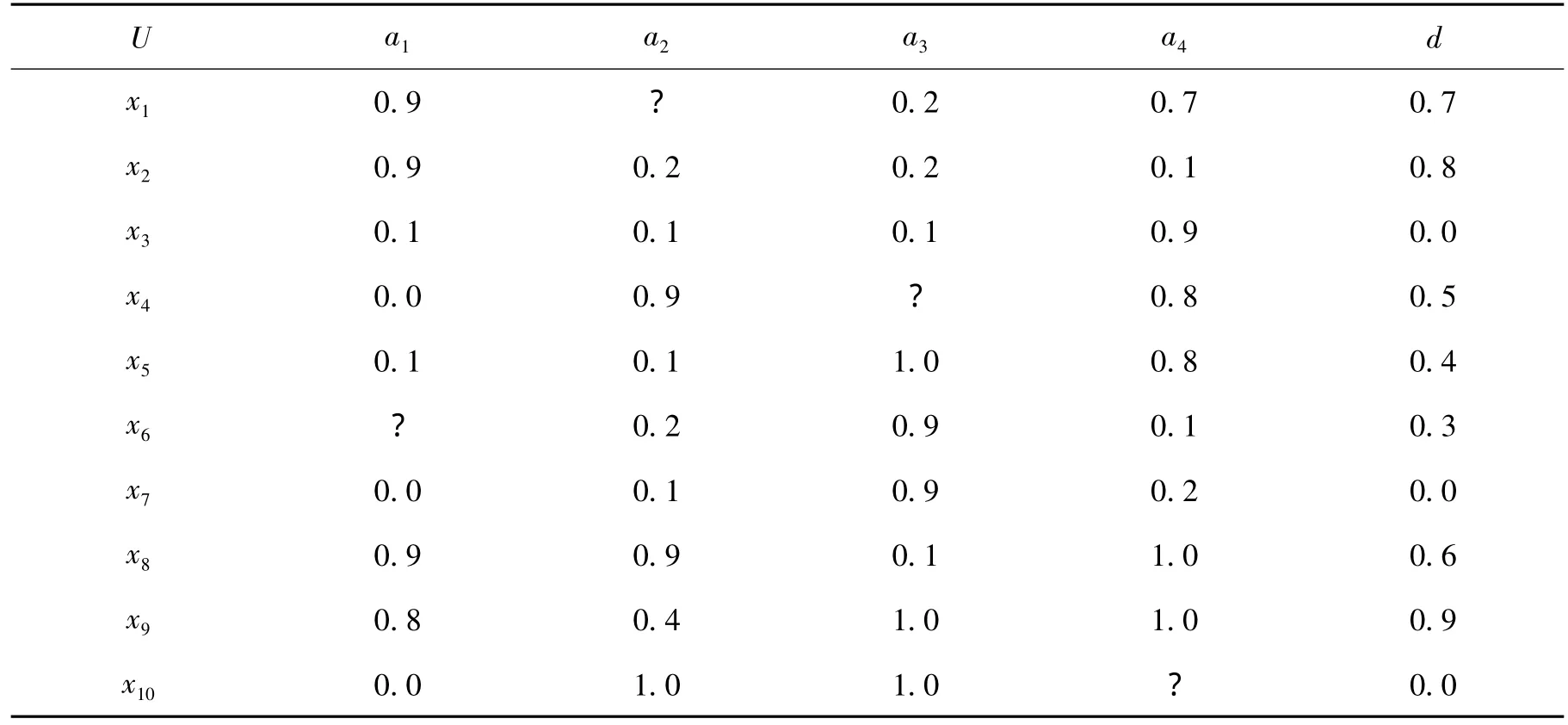
表1 不完备模糊序值决策系统
⑷因为d1∩d2⊆(d1,d2),根据(2)的结果,可以得到,即。其他公式可用类似方法证得。
在表1所示的不完备模糊序值决策系统中,AT={a1,a2,a3,a4}是条件属性集合,d 是决策属性。
根据定义5,可以得到表1中每个对象的模糊粗糙下、上近似隶属度如表2所示。

表2 表1中对象的模糊粗糙下、上近似隶属度
4 结束语
粗糙集理论在不完备信息系统中的扩展对于粗糙集理论的发展具有极其重要的意义。所讨论的不完备序值决策系统综合考虑了丢失型未知属性值和序值,因此具有更为广泛的应用前景。
由于粗糙集理论建立在分类的基础上,因此在本文所讨论不完备序值决策系统中,笔者提出了相似优势关系,这是非对称相似关系和优势关系的一种广义化表现形式。接着,笔者在不完备模糊决策系统中给出了基于相似优势关系的模糊粗糙集,并对其相关性质进行了研究。
在本文工作的基础上,笔者下一步的研究内容将是对基于相似优势关系的粗糙集和模糊粗糙集的约简问题进行讨论。
[1]Pawlak Z.Rough set theory and its applications to data analysis[J].Cybernetics and Systems,1998,29:661 -688.
[2] Pawlak Z.Rough sets and intelligent data analysis[J].Information Sciences,2002,147:1 -12.
[3]王国胤.Rough集理论在不完备信息系统中的扩充[J].计算机研究与发展,2002,39(10):1238-1243.
[4]Kryszkiewicz M.Rough set approach to incomplete information systems[J].Information Sciences,1998,112:39-49.
[5]Leung Y,Li.D.Maximal consistent block technique for rule acquisition in incomplete information systems[J].Information Sciences,2003,15:85 -106.
[6]Stefanowski J,Tsoukias A.Incomplete information tables and rough classification[J].Computational Intelligence,2001,17(3):545 -566.
[7]Wu W,Zhang W,Li H.Knowledge acquisition in incomplete fuzzy information systems via the rough set approach[J].Expert Systems,2003,20(5):280 -286.
[8]Greco S,Matarazzo B,Slowinski R.Rough approximation by dominance relations[J].International Journal of Intelligent Systems,2002,17(2):153 -171.
[9]Greco S,Matarazzo B,Slowinski R.Rough sets theory for multicriteria decision analysis[J].European Journal of Operational Research,2001,129(1):1 -47.
[10]Yang X,Yang J,Wu C,et al.Dominance - based rough set approach and knowledge reductions in incomplete ordered information system[J].Information Sciences,2008,178(4):1219 -1234.
[11]Shao M,Zhang W.Dominance relation and rules in an incomplete ordered information system[J].International Journal of Intelligent Systems,2005,20:13 -27.
[12]Luo G.,Yang X.Limited dominance - based rough set model and knowledge reductions in incomplete decision system[J].Journal of Information Science and Engineering,2010,26:2199 -2211.

