关于单变点Copula风险价值测度分析

余 平，史建红

(山西师范大学数学与计算机科学学院，山西临汾 041004)

风险管理是当今金融研究领域的一个重要课题，随着经济全球化和金融一体化进程加剧，全球经济、金融市场的相互依存性比以往任何时候都更加强烈，任何地区的金融市场的局部波动就可能迅速波及、传染、放大到全球市场，比如亚洲金融危机、美国次贷危机等等都是由于区域性金融演变成全球经济危机。因此金融机构要更好规避风险，提高竞争力，采用合理风险测度方法愈发重要。Value at Risk(VaR)[1]就是在90年代金融危机背景下应运而生，它在金融风险测量，监管领域中得到广泛的应用。

而在实际研究中，VaR计算都假定单个资产收益数据服从正态分布，不同的资产收益数据是线性相关性，大量文献[2－3]指出资产收益数据具有“尖峰厚尾”性，不同的资产收益数据之间还存在非线性相关性，这用传统方法计算VaR就显得不充分。Copula则可以很好地度量金融数据相关性，至Embrechts etc(1999)把Copula引入到金融数量分析以来，已经取得了很多有意义的成果。如国外Rosenberg etc(2004)运用Copula研究市场风险、信用风险和操作风险，结构表明Copula得到的VaR最接近经验VaR。国内吴振翔等 (2006)[4]利用Copula-Garch模型计算投资组合VaR，得出t-Copula很好描述金融变量相关性。陈守东等(2006)[5]将利用Copula和蒙特卡洛模拟计算不同置信水平下的VaR，计算结果Copula方法是要优于传统正态方法。

关于Copula计算VaR的文献还有很多，但是大多数文献都有一个共同的特点，都是假定选取的Copula的结构不变，也即是参数不变，而文献[6]都指出，采用Copula度量金融变量相关性还存在着变结构，也就是说金融变量在某个时刻前后Copula参数具有较大改变，如果再传统Copula理论计算VaR就不太合适。论文就讨论金融变量存在单变点的情况利用Copula进行风险价值测度。

1 Copula相关知识

Copula函数可以理解为“相依函数”或者“连接函数”，它是把多维随机变量的联合分布用其一维边际分布连接起来的函数。Copula理论的提出，不仅为我们提供了一条在不考虑边缘分布的情况下分析多元分布相关结构的途径，还为求联合分布函数提供了一条便捷的通道。Copula函数种类有很多，下面介绍一种常用的Archimedean Copula函数，Genest和 Mackay(1986)给出了 Archimedean Copula分布函数的定义如下:

定义 1 (Archimedean Copula)设 φ∶[0∶1]→ [0，R]为连续，严格递减的凸函数，φ(1)=0，φ(0)=∞，且具有连续，严格递减凸的逆函数 φ-1∶[0，∞]→[0，1]，φ-1(0)=1，φ-1(∞)=0，C(u，v)= φ-1(φ(u)+(φ(v))则称为由生成函数 (generator)，φ(·)生成的二元Archimedean Copula。

由此可见，Archimedean Copula由其生成函数φ(·)唯一确定，φ(·)不同可以得到不同的Archimedean Copula，具体见文献[7]，其中比较常用的一类是 GumbelCopula，其生成函数 φθ(t)=(-lnt)θ，由此得

2 Copula变点检测方法

设(U1，V1)，…，(Un，Vn)是[0，1]× [0，1]上的一列边缘分布为均匀独立的随机向量，其对应Copula函数为 C(u，θ1，η1)，C(u，θ2，η2)，…，C(u，θn，ηn)，其中(θi，ηi)∈（Θ(1)×Θ(2)）（i=1，2，…，n)为Copula中参数，这里将η看着常量参数，称为赘余参数(nuisance parameters)，则关于参数θ单变点的原假设和备则假设分别为:

和

和

如果拒绝原假设H0，则k*即为变点时刻。在这两个假设中，参数θ和k*都是未知的。如果k*=k已知的，此时，可以通过有关Copula的广义极大似然估计检验统计量来完成。如果检验统计量

取值较小，则拒绝原假设，这里c为C的密度函数。若记

等价于:

当存在着一个以上的变点时，可以采用文献[8]提出的二分分段法进行检测，其步骤如下:首先对全部样本序列检测单个变点，如果没有变点，则接受原假设，如果存在一个变点，则该变点可以将整个样本数据序列分成两个子样序列，然后对每个子样序列按第一步分别找出一个变点，继续这个分段过程，直到找到所有的子样序列的变点为止。

3 关于V aR，ES的M onte Carlo计算

VaR中文[1]译为“风险价值”或者“在险价值”，是在一定的置信水平下，某一资产或组合在未来特定的一段时间内最大的可能损失，表示式为:

其中，Δt为资产的持有期，α 为置信水平，VaRa，t+Δt表示在α分位数资产最大的预期损失。

ES(Expect Short)代表超额损失的平均水平，反映超过VaR时的可能遭受的平均潜在损失的大小，较之VaR更能体现潜在的损失。它不但具有VaR的优点，同时又具有良好的性质[3]。如ES满足正齐次性，次可加性，单调性，是一致性风险度量。其表达式为:

Copula模拟VaR，ES算法[5]

1)产生两个随机数（u,v）服从U(0,1)分布;

2)令所求的第一个随机数R1=F-1(u);

3)通过选定的Copula函数求得第二个序列在均匀分布上的随机数w=Cu-1（v）(其中Cu=∂C（u，v）/∂（u）;

4)计算第二个随机数R2=G-1(w);

5)通过前4步得到一对数据 (R1，R2)，将模拟进行n(相当大)次，就得到n对模拟的对数收益数据 (R1，R2)，然后将模拟产生的随机数以等权组合计算不同置信水平下的VaR和ES。

4 实证研究

为了考察上海股市和深圳股市的之间的关系，文中选取上证综合指数(SHI)和深圳成份指数(SZI)每日收盘价为样本研究对象，选取样本时间段为:19990105－20090521，共2501组数据。

4.1 数据描述

将价格定义为市场每日收盘价，将收益率Rt定义为:Rt=100*(log(Pt)-log(Pt-1))，则收益数据共2500组数据。

由图1可以看出两股票市场收益呈尖峰性和波动聚集性，从表1可以看出具有一定偏斜度，峰度大于3，具有厚尾性.因此两股市收益率具有尖峰厚尾特点，且呈不对称性，如果选择正态分布来描述就会低估风险。

图1 沪深股票指数日对数收益波动率图

表1 各股票指数和等权组合的描述统计

4.2 参数估计及变点检测

由4.1知收益数据具有尖峰厚尾特点，而Laplace分布可以较好度量收益尖峰厚尾性，因此文中选择Copula的边缘分布函数为Laplace分布，其分布函数和密度函数如下[9]:

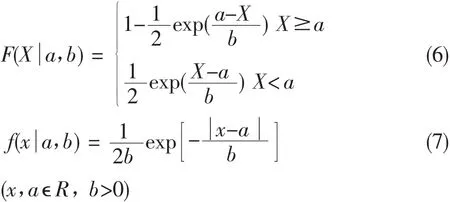
采用极大似然估计方法的对收益变量边缘分布的参数a，b见表2。

表2 两股票日对数收益边缘分布的参数极大似然估计

在本文中，为了更好分析上海股市和深圳股市的相关结构，首先应该寻找最合适的Copula函数进行分析。大量文献如 [6]证明Gumbel Copula能很好地描述相关结构，因此文中只选Gumbel Copula进行数据的估计和拟合，其它Copula可以相类似分析。

采用文中第2部分介绍变点检测方法对沪深股市对数收益数据进行分析，同时采用极大似然估计法对整个收益数据的参数及其有变点后参数进行估计，得到单变点时刻和关于Gumbel Copula参数估计如下。

表3 变点参数估计

通过变点检测方法得到沪深股市对数收益数据参数θ发生时刻为20070716，探究其原因，我们不难联想到与美国发生的次级债金融危机有关，2007年4月2日，作为美国第二大次级抵押贷款公司—新世界金融公司面对来自华尔街174亿美元的逼债宣布申请破产保护，由于投资者对次级贷款危机和房地产市场的担忧席卷华尔街，美国股指7月26日收盘暴跌，道琼斯工业平均指数下跌300多点。受此影响，亚太股市27日纷纷下挫，日经指数跌幅较大，而澳大利亚、韩国等股指更是创造当年以来最大当日跌幅。2007年8月7日，中行、工行也卷入美国次级危机。从表2给出变点时刻来看，这与次级贷款危机产生影响的时刻基本上相一致。

4.3 VaR和ES计算

在传统的利用Copula技术计算风险价值VaR的文献中，都没有考虑到Copula有变结构的情况，如果认为有关Copula的参数是保持不变，这可能低估VaR，因此论文就考虑2种不同情况——即一种是无变点结构，另一种有变点结构的风险测度。

为了计算方便，资产组合由等额的上证综指和深圳成指组成，采用文中第4部分介绍的方法进行Copula模拟VaR，ES的计算。选取时间段从19990105－20090521的收益数据总共2500组，而参数发生变点时刻为 20070716，从 19990105－20070716共有2050组收益数据，从20070716－20090521共450组收益数据，因此在模拟收益数据时变点前后数据比例为2050:450，最后再把变点结构前后数据合并起来计算VaR，ES。

在t时间资产组合的价值，

Vt=0.5P1，t+0.5P2，t，对于模拟对数收益 Ri，j(i=1，2；1≤j≤n在时间范围 [t，t+1]完成 n次模拟，假设资产组合在未来的权数不变，则下一时刻 t+1 的 资 产 价 值 为 Vt+1=0.5P1，texp(R1，t+1/100)+0.5P2，texp(R2，t+1/100)∶对于每次模拟 j，计算出资产组合价值的变换

构造的的 xt= { xt，j}分布函数就是样本在时间[t，t+1]模拟的资产收益的分布函数。

由式(8)和VaR和ES的定义,可以得到组合收益在t+1时刻的VaR和ES表达式分别为

其中，α为估计的置信水平，x*t+1(r)为第 r个按上升次序排列的模拟组合收益数，Nt+1为模拟的不超过-VaRt+1的个数，I为示性函数。n=5000，模拟计算结果见表4。

从表4中可以看出，ES反映超过VaR时的可能遭受的平均损失，在不同置信度下，计算VaR绝对值都小于ES绝对值，同时在没有考虑Copula的变结构情况下计算VaR，ES绝对值要略低于考虑Copula的变结构VaR，ES。

表4 日VaR，ES估计

5 结语

文中考虑到金融收益数据的尖峰厚尾性和Copula可能存在着变结构等特点，选择边缘分布为Laplace分布描述收益数据的尖峰厚尾性，采用变点分析的方法对Gumbel Copula变结构进行研究，从而计算出在不同置信水平下投资组合的风险价值和期望损失，和传统没有考虑Copula变结构进行风险价值测度相比，考虑Copula变点更加合理.当然文中选取是Gumbel Copula进行分析研究，对于其它Copula函数如Clayton Copula，Frank Copula等该方法也是适用的.不知之处是文中只考虑opula单变点情况，对于多变点的情形可以采用类似的方法进行风险价值测度。

[1]菲利普·乔瑞著，陈跃.风险价值VAR[M].2版.上海:中信出版社，2005.

[2]Artzner P，Delbaen F，Eber J-M.et al.Coherent Measures of risk[J].Mathematical Finance，1999(9):203-228.

[3]Kevid Dowd.Measuring Market Risk.2nd Edition[M].New York:John Wiley&Sons，Ltd，2005.

[4]吴振翔，陈敏.基于Copula—GARCH的投资组合风险分析[J].系统工程理论与实践:2006(3):45-52.

[5]陈守东，胡铮洋，孔繁利.Copula函数度量风险价值的Monte Carlo模拟[J].吉林大学社会科学学报，2006(3):85-91.

[6]Dlas A.Copula Inference for Finance and Insurance[D].Doctoral Thesis，ETH，2004.

[7]Nelson R B.An introductions to copulas[M].New York:Springer，1999.

[8]Vostrikoval.Detecting distorder in multidimensional random processes[J].Soviet Mathematics，Doklady，1981.

[9]唐俊林，杨虎.深沪股市收益率分布特征的统计分析[J].数理统计与管理:2004(5):1-4.