线性变换及其矩阵表示

张姗梅，刘耀军

（1.太原师范学院数学系，山西太原030012；2.太原师范学院计算机系，山西太原030012）

我们知道,取定有限维线性空间V的一个基,则V中向量的运算及向量间的关系的讨论可转化为向量坐标的讨论。同样,取定V的一个基,则V的线性变换的讨论可转化为其矩阵的讨论。本文通过一些实例说明,借助矩阵工具可方便解决有关线性变换的问题,反过来,利用线性变换解决某些矩阵问题往往变得比较容易。

设V是数域 P上 n维线性空间,α1，α2，…，αn是V的一个基,σ是V的一个线性变换,若（σ（α1），σ（α2），…，σ（αn））＝（α1，α2，…，αn）A，则称 A 为线性变换 σ 在基 α1，α2，… αn下的矩阵。

定理1 设 α1，α2，…，αn是数域P上n维线性空间V的一个基,则 f：σ→A(A是 σ 在基 α1，α2，…，αn下的矩阵）是V的线性变换集L（V）到P上n阶矩阵集Pn×n的一个双射。并且如果σ,τ∈L（V），而σ→A，τ→B，那么

σ＋τ→A＋B，στ→AB，aσ→aA（a∈P）。

定理1告诉我们,研究数域P上n维线性空间V的线性变换与研究Pn×n的矩阵没有什么本质的不同。由于矩阵的运算很具体,容易实现,因此将线性变换的讨论归结为矩阵的讨论,常使问题容易得到解决。

例1 用P［x］n表示数域P上次数小于n的多项式的全体添上零多项式所成的线性空间,设P［x］n的全体线性变换所成的线性空间为M,D为 P［x］n的微商变换（即D（f（x））＝f′（x）,对∀f（x）∈P［x］n，且记M中与D可交换的线性变换的集合为N,即

N＝｛T∈M｜DT＝TD｝，

则N构成M的子空间。求N的维数及其一个基。

解 D∈M,取 P［x］n的一个基 1,x，x2/2！，…，xn－1/（n－1）！，则 D 在此基下的矩阵为

设T∈M在所给基下矩阵为B＝（bij）,则

TD＝DT⇔AB＝BA

⇔bi＋1，j＝bi，j－1，bn，j－1＝0，bi＋1，1＝0（i＝1，2，…，n－1；j＝2，3，…，n）

由于

b11B1＋b12B2＋…＋b1nBn。

并且B1，B2，…，Bn线性无关。 因此若设Ti∈M在所给基下的矩阵为Bi,则T1，T2，…，Tn是N的一个基,N的维数为n。

例2设σ，τ是n（n≻0）维线性空间V的线性变换,证明:στ－τσ≠ε，ε是V的单位变换。

证明 取 V 的一个基 α1,α2，…，αn，设 σ，τ 在这个基下的矩阵分别为A＝（aij），B＝（bij）。则στ－τσ在这个基下的矩阵为AB－BA,而单位变换ε在该基下的矩阵为单位矩阵E。由 tr（AB－BA）＝tr（AB）－tr

以及tr（E）＝n可知AB－BA≠E,所以στ－τσ≠ε。

例3设σ是n维线性空间V的一个线性变换,存在V的基,使σ在该基下的矩阵为对角形,λ1，…，λs是σ的所有不同的特征值。 证明存在V的线性变换σ1,…，σs，使为单位变换,且 i≠j时 σiσj＝0 而 σ2j＝σj，j＝1，2，…，s。

证明 由已知,可设 σ 在V的基 ε1，ε2，…，εn下的矩阵为对角阵

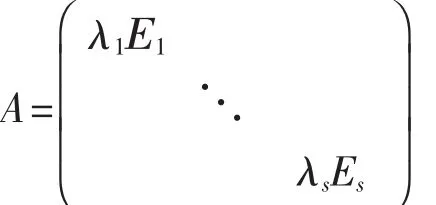
其中Ei为ni阶单位矩阵,则

σ（ε1，ε2，…，εn1）＝（ε1，ε2，…，εn1）λ1E1

σ（εn1＋n2＋…＋ns－1＋1，…，εn）＝

并且 A1＋…＋As＝E,当 i≠j时 AiAj＝0 而 A2j＝Aj，j＝1，2，…，s。

所以作V的线性变换 σi,使 σi在基 ε1，ε2，…，εn下的矩阵为Ai,则为单位变换),且 i≠j时 σiσj＝0 而 σ2j＝σj，j＝1，2，…，s。

例4 设σ，τ是数域P上n维线性空间V的线性变换,则στ与τσ有相同的特征值。

证明 取V的一个基 α1，α2,…，αn，设 στ在这个基下的矩阵分别为A，B,则στ与τσ在同一基下的矩阵分别为AB与BA，由线性变换特征值的求法,要证στ与τσ有相同的特征值,只需证AB与BA有相同的特征多项式。由

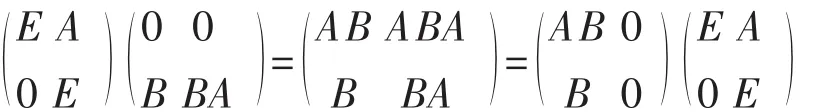
得

根据相似矩阵有相同的特征多项式,有

即

定理2 设线性变换σ在基α1，α2,…，αn下的矩阵是A,向量ξ在基α1，α2,…，αn下的坐标是（x1，x2，…，xn）。若 σ（ξ）在基 α1，α2,…，αn下的坐标是（y1，y2，…，yn）,则

例5设σ是n维线性空间V的线性变换,则σ的秩+σ的零度＝n,即

dim（σ（V））＋dim（σ－1（0））＝n。

证明 设σ在V的基α1，α2,…，αn下的矩阵为A,则

（σ（α1），σ（α2），…，σ（αn））＝（α1，α2，…，αn）A于是向量组 σ（α1），σ（α2），…，σ（αn）的秩等于矩阵 A 的秩,而 σ（V） 作为 σ（α1），σ（α2），…，σ（αn））所生成的子空间 L（σ（α1），σ（α2），…，σ（αn））,其维数等于向量组σ（α1），σ（α2），…，σ（αn）的秩,因此dim（σ（V））＝r（A）。

另一方面,由定理2,

因为齐次线性方程组AX＝0的解空间的维数n－r（A）,因此dim（σ－1（0））＝n－r（A）。所以dim（σ（V））＋dim（σ－1（0））＝r（A）＋（n－r（A））＝n。

由例5的证明及矩阵秩的性质,可得。

例6 设σ，τ是n维线性空间V的线性变换。证明στ的秩≥σ的秩＋τ的秩－n。

证明 设 σ，τ在 V 的基 α1，α2，…，αn下的矩阵分别为 A，B。则 στ在基 α1，α2，…，αn下的矩阵为AB,于是由例5知,στ的秩＝r（AB）,σ的秩＝r（A）,τ的秩＝r（B）。由于

r（AB）≥r（A）＋r（B）－n。

所以στ的秩≥σ的秩＋τ的秩－n。

例7 设σ，τ均为n维线性空间V的线性变换,若 dim（σ（V））＋dim（τ（V））＜n，则 σ 与 τ有公共的特征向量与特征值。

证明 设 σ，τ在 V 的基 α1，α2，… αn下的矩阵分别为A，B。则

dim（σ（V））＝r（A），dim（τ（V））＝r（B）由已知条件可得 r（A）＋r（B）＜n,而r（B）＜n,因而线性方程组有非零解,设为X0,则由此得 AX0＝0，BX0＝0。 令 α＝（α1，α2,…，αn）X0,则 α≠0,且由定理 2 知,σ（α）＝0＝0·α,τ（α）＝0＝0·α，因而 α 为 σ，τ公共的特征向量,0为公共的特征值。

上面的例子是将线性变换的问题转化为矩阵问题,用矩阵理论予以解决。但有时也需要将矩阵问题转化为线性变换来研究。

例8证明:n阶矩阵

的最小多项式为

d（x）＝xn＋a1xn－1＋…＋an－1x＋an。

证明 取一n维线性空间V以及V的一个基α1，α2,…，αn，作V的线性变换σ,使σ在V的基α1，α2,…，αn下的矩阵为 A。则

σ（α1）＝α2，σ（α2）＝α3，…，σ（αn－1）＝αn，σ（αn）＝－anα1－an－1α2－…－a1αn。

于是αi＝σi－1（α1），i＝2，3，…，n。这样,对任意次数小于n的多项式

f（x）＝b0xm＋b1xm－1＋…＋bm－1x＋bm（b0≠0，m＜n）由 α1，α2,…，αn线性无关,得

f（σ）（α1）＝（b0σm＋b1σm－1＋…＋bm－1σ＋bmε）（α1）＝

b0αm＋1＋b1αm＋…＋bm－1α2＋bm（α1）≠0

因此f（σ）≠0,从而f（A）≠0。又d（σ）（α1）＝（αn＋a1σn－1＋…＋an－1σ＋anε）（a1）＝σ（αn）＋a1αn＋…＋an－1α2＋anα1＝（－anα1－an－1α2－…－a1αn）＋a1αn＋…＋an－1α2＋anα1＝0进一步有

d＝（σ）（α1）＝d（σ）（σi－1）（α1）＝

σi－1（d（σ）α1）＝0，i＝2，3，…，n。

因此 d（σ）＝0,从而 d（A）＝0。这就证得 d（x）是 A 的最小多项式。

例9设A是一个n阶矩阵，A2＝A。

证明 A与对角矩阵相似。

证 设n维线性空间V的线性变换σ在V的基α1，α2，…，αn下的矩阵为A。下证,σ在V的一个适当的基下的矩阵是对角矩阵。这样,由同一线性变换在不同基下的矩阵相似,也就证明了所要的结论。

由 A2＝A,可知 σ2＝σ 于是,对任意 α∈V,有α＝σ（α）＋（α－σ（α））,其中 σ（α）∈σ（V）,而 α－σ（α）∈σ－1（0）（σ（α－σ（α））＝σ（α）－σ2（α）＝0,因此V＝σV＋σ－1（0）。又设β∈σV∩σ－1（0）,则存在ξ∈V使β＝σ（ξ）＝σ2（ξ）且σ（β）＝0，因而β＝σ（ξ）＝σ2（ξ）＝σ（β）＝0，所以V＝σV⊕σ－1（0）。取σV的一个基η1,…，ηn再取σ－1（0）的一个基ηr＋1,…，ηn，则η1，…，ηr，ηr＋1,…，ηn是V的一个基,且由σ（ηi）＝ηi，i＝1，2，…，r；σ（ηj）＝0，j＝r＋1，…，n。

知σ在这个基下的矩阵是对角矩阵。

例10设A，B是数域F上的n阶矩阵,求证:方程组AX＝0与BX＝0同解的充分必要条件是存在 F上可逆矩阵P,使B＝PA。

证明 因P是可逆阵,充分性是显然的。下证必要性。

令V＝Fn是数域F上的n维列向量空间。作V的线性变换 σ：X→AX与 τ：X→BX,则 σ，τ在V的基

e1＝（1 0 … 0）′

e2＝（1 0 … 0）′，…，en＝（0 0 … 1）′

下的矩阵分别为 A，B;且 σ－1（0）＝｛X∈V｜AX＝0｝，τ－1（0）＝｛X∈V｜BX＝0｝。

若方程组 AX＝0 与 BX＝0 同解,即 σ－1（0）＝τ－1（0）。由例 5,如果 r（A）＝r(这时 r（B）＝ r）,那么 dim（σ－1（0））＝n－r，dim（σ（V））＝r。取σ－1（0）的一个基αr＋1,…，αn。将它扩充为 V 的一个基:α1，…，αr，αr＋1，…，αn。由σ（αj）＝0，j＝r＋1，…，n知σ（αi），…，σ（αr）生成σ的值域σ（V）,但dim（σ（V））＝r,因此σ（α1），…，σ（αr）作成σ（V）的一个基。同理τ（α1），…，τ（αr）作成τ（V）的一个基。现将σ（α1），…，σ（αr）扩充为V的基σ（α1），…，σ（αr），fr＋1，…，fn。再将τ（α1），…，τ（αr）扩充为V的基τ（α1），…，τ（αr），gr＋1，…，gn。作V的线性变换φ,使

φ（σ（αi））＝τ（αi），i＝1，…，r；

φ（fj）＝gj，j＝r＋1，…，n

则φ是V的可逆变换,且φσ（αi）＝τ（αi），i＝1，…，r;φσ（αj）＝0＝τ（αj）,j＝r＋1，…，n所以φσ＝τ。令φ在V的基e1，e2，…，en下的矩阵为P,则P是F上可逆矩阵且PA＝B。

[1]张禾瑞,郝炳新.高等代数[M].5版.北京:高等教育出版社,2007.

[2]姚幕生.高等代数[M].上海:复旦大学出版社,2002.

[3]郭聿琦,岑嘉评,徐贵桐.线性代数导引[M].北京:科学出版社,2001.

[4]刘小川,何美.幂等矩阵与秩幂等矩阵的充要条件[J].山西大同大学学报:自然科学版,2011,27(1):9-11.

[5]王莲花.矩阵与其友矩阵相似的一个充要条件及其证明[J].大学数学,2010,26(5):161-163.

[6]杨忠鹏,王海明,张金辉,等.关于线性变换的可交换问题的一些讨论[J].北华大学学报:自然科学版,2010,11(4):307-311.

[7]黄弘.一类矩阵的对角化与秩的恒等式[J].山西师范大学学报:自然科学版,2010,24(1):21-24.