一类拟线性薛定谔方程解的爆破

胡文燕

（晋中学院数学学院，山西晋中 030600）

薛定谔方程是量子力学的基本方程，它揭示了微观物理世界物质运动的基本规律，它同时拥有与抛物线方程和双曲型方程类似的性质。近些年来，薛定谔方程受到了许多数学工作者的广泛关注，不仅因为它在非线性光学领域有着广泛的应用，而且有很多模型简化后，都是一些确定的非线性薛定谔方程，我们考虑如下拟线性薛定谔方程的初值问题：

其中，(x,t)∈RN×R,u:RN×R→C是一复值函数，△是标准的N维Laplace算子，且p＞2，i2=-1,β,θ:RN→R均为实值函数，u0(x)是光滑的，并且

此时

对于上述问题，前人已经作了一些研究，得出了一些结果，在文献[1-2]中介绍了驻波解的存在性，文献[3－5]对该问题初值的局部适定性及全局适定性进行了探讨。郭柏灵等人对该初值问题解的爆破现象进行了研究，得出了如下结论[6]：

定理1假设u(t)∈W2,2(RN)(N≥1)是初值问题（1）的解，并且

1）u0(x)∈W2,2(RN)(N≥1),β≥0,θ＞0,且≤p＜2·2*:=2×2*。 这里，若 N≥3,则若N＜3，则2*=∞；

从而，存在T0＞0,使得

定理1的证明过程请参看文献[6]。需要特别指出的是，在上述结论的证明中，要求L2(RN)，这就对初值u0有了限制。为能将结论应用到更多的初值中，我们将其推广到各向异性空间（所谓各向异性空间，是指空间不对称的情形）中去。

下面，对各向异性空间中拟线性薛定谔方程解的爆破进行研究，可得如下结论：

引理1如果u(t)∈H2(RN)是初值问题（1）的解，那么

2)H(u(t))=H(u0),∀t∈R。

定理2如果u(t)∈H2(RN)是初值问题（1）的解，而且1)u0(x)∈H2(RN), β≥0,θ＞0,且当N=3时,;当N≠3时，2*=∞；

其中，y=(x1,…,xN-K),x=(y,xN-K+1,…,xN)

从而，存在T0＞0,使得初值问题（1）的解在有限时刻T0爆破。更多地，若

则 T0≤ T*,其中

此时

其中，y=(x1,…,xN-K),x=(y,xN-K+1,…,xN)于是有

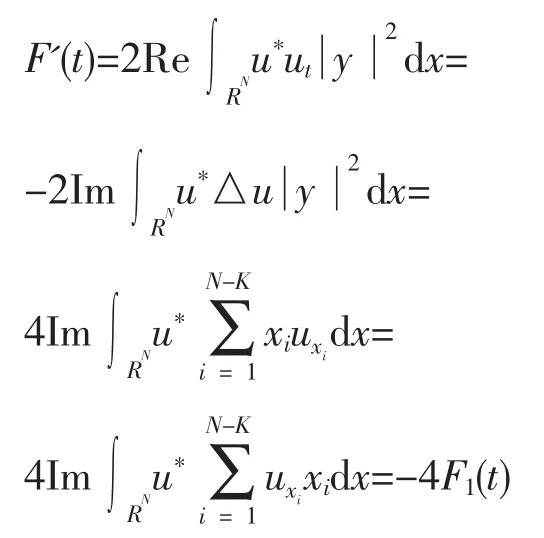
经换算，

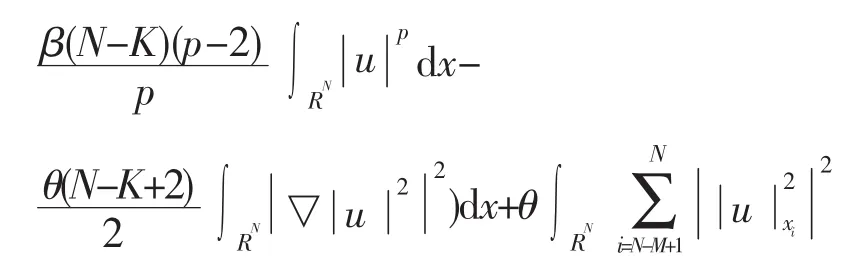
由 H(u(t))=H(u0)β＞0,θ＞0，有 F'1(t)≥0。即

从而可证得解u在有限时刻T0爆破。而且由

可得

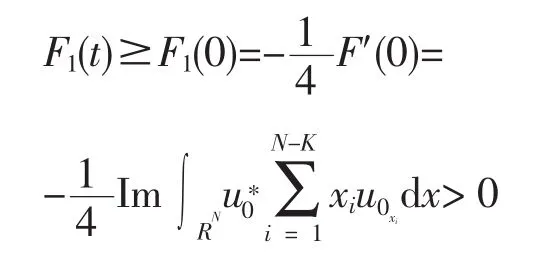
从而，F'(t)=-4F1(t)＜0，且

由Hölder不等式，得

从而

证毕。

至此，我们得出了在各向异性空间中，拟线性薛定谔方程的解在有限时间内会爆破。

[1]Lin J Q,Wang Y,Wang Z Q.Soliton solutions for quasilinear Schr?dinger equations[J].J Diff Eqns,2003:407-426.

[2]JLin Q,Wang Y，Wang Z Q.Solutions for quasilinear Schrodinger equations via Nehari method[J].Commun Partial Differ.Eqns,2004,29:879-901.

[3]T Kato.On nonlinear Schr?dinger equations,II.Hs-solutions and unconditional well-posedness[J].J d′Analyse Math，1995,67:281-306.

[4]H Lange,M Poppenperg，H Teismann.Nash-Moser methods for the solutions of quasilinearSchr?dinger equations[J].Commun.Partial Differ Eqns,1999,24:1399-1418.

[5]M Poppenberg.On the local well posedness of quasilinear Schr?dinger equations in arbitrary spacedimension[J].J Diff.Eqns,2001:83-115.

[6]Guo Boling,Chen Jianqing，Su Fengqiu.The"Blow up"problem for a quasilinear Schr?dingerequation.Journal of mathematical physics 46,073510[P].2005.