基于微型三轴仿真转台的误差分析
马 炎,李世中,崔瑞男
MA Yan,LI Shi-zhong,CUI Rui-nan
(中北大学 机电工程学院,太原 030051)
0 引言
仿真转台作为仿真技术的关键设备,其发展历程经历了从早期的单轴到双轴、双轴到三轴的几个阶段。三轴转台通过对空中飞行目标的动力学特性进行模拟,可以完成对空中飞行目标的姿态复现,并可以对其传感器件、制导与控制系统以及相关执行机构进行测试。仿真精度是仿真转台的重要指标,但由于受到环境变化和制造误差、控制因素以及力负载等多种因素的影响,半实物仿真系统中的关键设备一转台(主体结构是内、中、外三框分别模拟翻滚、俯仰、偏航动作),其实际运动路线和理想状态间存在误差,而整个系统的仿真精度将受此误差的影响。影响转台仿真精度的主要因素包括指向误差、速率稳定度误差、幅相误差等[1]。故相当有必要对转台进行误差分析。
1 转台的指向误差分析
1.1 指向误差的定义及其建模
指向误差实际上是一种空间角度误差,通常指的是固连在内框(如图1所示),上的单位向量在经过转台的转动后,预期指向和实际指向之间的偏差,此误差将影响整个系统的定位精度。

其中R1(Ω)为欧拉变换矩阵

图1 立式转台结构示意图

转台转动产生的误差E主要由下面两个方面的因素引起:即轴系误差和几何运动误差。其中轴系误差主要是由三个轴的装配正交度和不同心引起的正交误差(设为),几何运动误差轴的回转精度(设为)和位置控制精度(设为)以及轴摆动引起的相对误差(设为)。此相对误差指的是X、Y、Z三轴因轴的摆动从而引起在Y-Z、Z-X、X-Y平面上的投影分别与Y、Z、X的夹角,定义为W4、W5、W6。有:

则指向误差可以描述为:

上式中的ΔR=R2(Ω,E)-R1(Ω)。
指向误差如图2所示

图2 指向误差
1.2 指向误差的算法
在理想情况三轴仿真转台的内、中、外三轴分别绕X、Y、Z轴依次转动w1、w2、w3的角度,此时固连在内框上的单位向量将变成:有

在建模过程中,先将固定矢量连同内框架绕X轴转动-W4角,然后绕Z轴转动β1角,再绕X轴转W4角,中框与外框以此类推。在绕内框轴X转动而同时以内框轴为基准时则无指向误差。
在转动各环轴时加入各轴的位置控制精度γ1、γ2、γ3,即得到实际的含误差因素的欧拉变换式。定义中间变量A、B、C、D、M 。其含义如下:
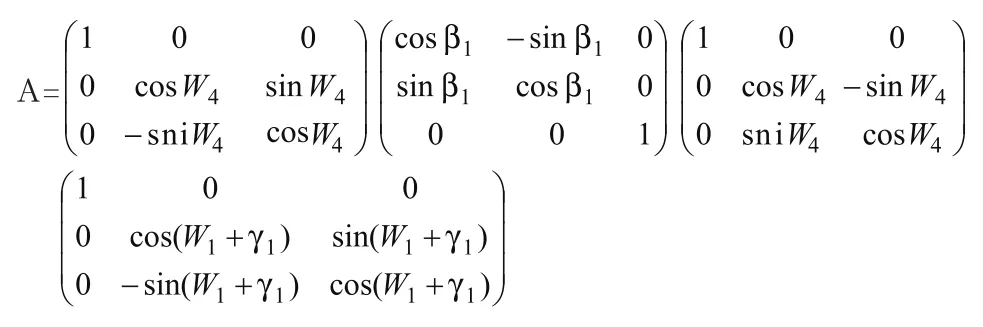

故可得欧拉变换:

由R1(Ω)、R2(Ω,Ε)可算出ΔR,最后由式(4)可得 Δφ。
2 转台的速率稳定度误差分析
由于受转台系统非线性畸变因素的影响,转台最小角速度并不是一个固定的值,每次测量都可能不一样[3]。由于在转台设计时对最小角速度有要求,因此可以用速率稳定度来限制角速度的跳动。
常用两种方法来研究速率稳定度:其一是用随机采样过程进行描述,即通过一固定的采样间隔得到用一定时间间隔得到的瞬时角速度值来描述其速率稳定度;其二是用瞬态过程描述,即利用瞬时角速度对速率稳定度作近似描述。其实第二种方法是第一种方法的特例即当时间间隔趋近零时的情况。前者的方差是平均速率稳定度,后者是瞬时速率稳定度,二者通过θ(t)联系。计算平均速率稳定度的公式如下:
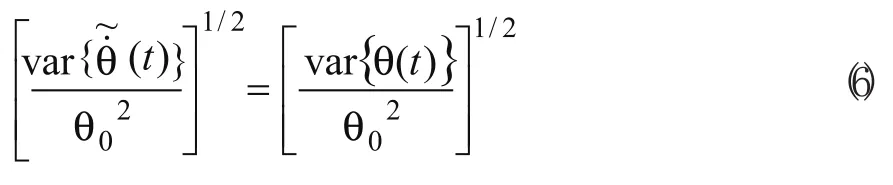
上式中:θ0是采样间隔位置量,单位是rad
3 转台的幅相误差
本转台事实上它并非是一个无惯性的放大环节(非理想转台),可以通过内、中、外三框的闭环传递函数得到对数幅频特性。表1为在截频处的幅相误差(实测数据和计算数据)。由此表可知系统存在幅值衰减和相位滞后。
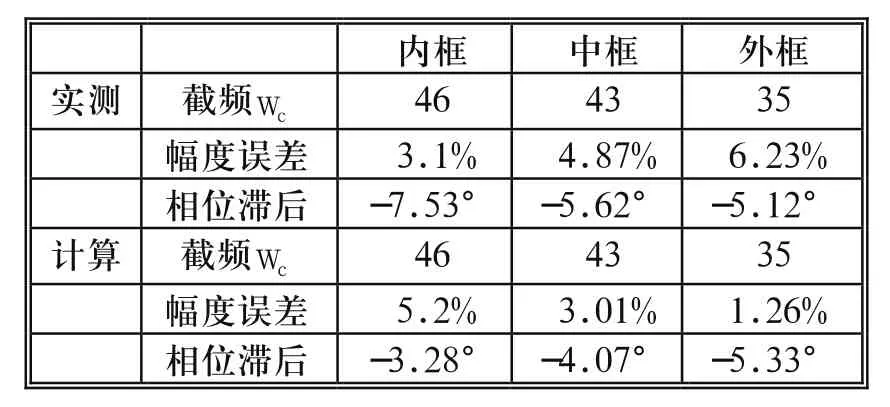
表1 实测与计算数据对比
4 误差相关性分析
4.1 相交度对中心位置的影响
图3中为各轴转动30度时,三项相交度误差对转台内轴中心位置的影响。

图3 相交度误差对设备中心位置的影响
4.2 回转误差对指向误差的影响
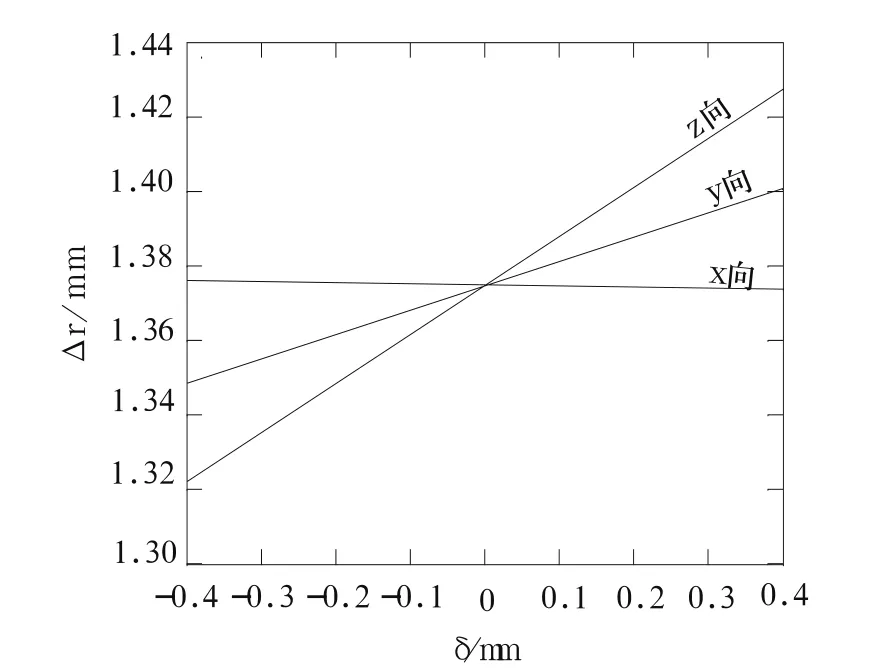
图4 轴向和径向误差对中心位置误差的影响
5 结论
1)在影响指向误差的因素中,影响最大的是正交度误差而位置精度则次之,回转精度的影响最小,由于本转台系统在低速下运行故其轴的摆动误差可以忽略。
2)由于正交度误差对指向精度的影响较大而对回转精度影响不大,因此应提高正交度误差相对减小回转度误差可提高系统的仿真精度。
3)由于本转台系统在低速下运行,其速率稳定度误差同样可以忽略。
4)幅相误差会造成系统的幅值衰减和相位滞后。
[1] 李强.三轴仿真转台设计及动力学研究[D].哈尔滨工程大学,2007.
[2] 宋涛.射频仿真系统中目标阵列的误差分析[D].南京航空航天大学,2008.
[3] 肖卫国.三轴飞行模拟转台误差研究[J].系统仿真学报,2001.

