新型抗空泡翼型剖面设计研究
戈 亮 龙 文 谢 伟 杨向晖 邱辽原
1海军装备部 装备采购中心,北京100071 2中国舰船研究设计中心,湖北 武汉430064
新型抗空泡翼型剖面设计研究
戈 亮1龙 文2谢 伟2杨向晖2邱辽原2
1海军装备部 装备采购中心,北京100071 2中国舰船研究设计中心,湖北 武汉430064
基于Eppler翼型设计方法提出一种新的抗空泡翼型剖面设计方法。新的设计方法利用预先给定的最大厚度和设计升力系数进行翼型剖面设计,并将厚度及拱度的分布与攻角的设置相结合,将所需的厚度与拱度分布转换为合理的攻角分布作为输入,以便用Eppler方法进行翼型剖面设计,并通过对攻角分布进行修改来调整空泡斗的位置。计算表明,所提出的方法对控制翼型剖面的厚度和拱度分布有效,利用该法设计的翼型剖面具有较好的空泡性能。
翼型剖面;保角变换;空泡
1 引言
Eppler方法是德国斯图加特大学的R.Eppler教授于20世纪50年代中期提出的一种基于保角变换的翼型剖面设计方法[1-2]。自20世纪80年代以来,人们将Eppler方法应用于水翼剖面和螺旋桨桨叶剖面的设计,取得了不少进展[3-6]。利用Eppler方法设计出来的新翼型剖面有较好的抗空泡性能。
但Eppler方法是一种根据指定的速度分布形式来进行设计的翼剖面设计理论,其设计输入参数主要为翼型表面的攻角分布和与压力恢复有关的参数。输入参数均用来控制速度分布的形式。从输入参数中无法知道设计出的翼型的厚度分布与拱度分布等翼型剖面几何参数信息。如果设计出的翼型剖面几何特征不满足要求,则需对输入参数进行修改以满足要求。由于速度分布形式与剖面几何特征之间并不存在明显的联系,所以这一项工作往往十分繁琐。并且翼型剖面的抗空泡性能与其在一定攻角范围内的速度分布的形式直接相关,如果为了得到所需要的几何参数而对速度分布形式进行修改,有可能使得剖面的抗空泡性能下降。
进行螺旋桨设计时,桨叶剖面的最大厚度以及厚度分布、拱度分布等几何特征和设计升力系数由螺旋桨设计理论确定[7]。因此,为了将Eppler方法设计的翼型剖面直接用于螺旋桨设计,在进行剖面设计时,要求设计出的剖面具有指定的厚度和设计升力系数。而且为了使设计出的桨叶剖面具有较好的抗空泡性能,需要对桨叶剖面的厚度分布以及拱度分布进行一定的调整,且在一定的攻角范围内的速度分布形式必须有利于推迟空泡产生。由于Eppler方法输入参数众多,参数的设置较为复杂,如果没有一定的方法对其进行控制,必将使得工作量繁重且难以达到设计指标。
据此,本文提出了一种设计方法,能够有效地调整设计参数,使得设计出的翼型剖面具有指定的厚度比和设计升力系数,大大简化设计工作。同时,通过合理地设置翼型表面的攻角分布以有效地控制拱度分布和厚度分布,使得设计出的翼型剖面具有较好的抗空泡性能,并能够根据需要修改设计参数对翼型空泡斗的位置进行调整,从而克服翼型剖面设计和螺旋桨设计之间的矛盾。
2 Eppler翼型设计理论简介
Eppler方法是根据指定的速度分布形式通过保角变换来得到所需的翼型剖面。保角变换示意如图1所示。为了使映射出的翼型存在并且有实际意义,指定的速度分布形式并不能完全任意。在Eppler方法中,指定的速度分布形式均采用Wortmann形式的速度分布。该方法可以将翼型表面分为若干部分,在每一部分上指定一个攻角和速度分布形式,可以考虑翼型剖面在多个工况下工作的情况,因此是一种多点设计方法,特别适用于来流攻角变化的情况。翼型表面在单位圆上的区域划分以及对应的攻角设置如图2所示。为了使设计出的翼型尾缘闭合,Eppler方法特意在速度分布形式中引入了尾缘闭合因子来控制翼型尾缘的形状。
在Eppler方法中,将翼型剖面设计和边界层计算结合起来。利用二维面元法对设计出的翼型计算其在指定攻角下的速度分布。根据计算出势流速度分布,利用差分方法求解翼型表面边界层动量方程和能量方程。解出边界层的动量厚度和能量厚度后根据经验公式来判断边界层是否发生分离。

图1 保角变换示意图Fig.1 Conformal mapping
3 新的剖面设计方法
由于Eppler方法的设计输入参数是单位圆上的区域划分和攻角设置,难以将这些输入参数同翼型本身的几何特征联系起来。而螺旋桨桨叶剖面的设计却以厚度分布和拱度分布为主要关注对象。为了克服这个困难,需要确定攻角设置和厚度拱度分布之间的联系。
由文献[1]可知,翼型表面纵坐标可利用下式计算:
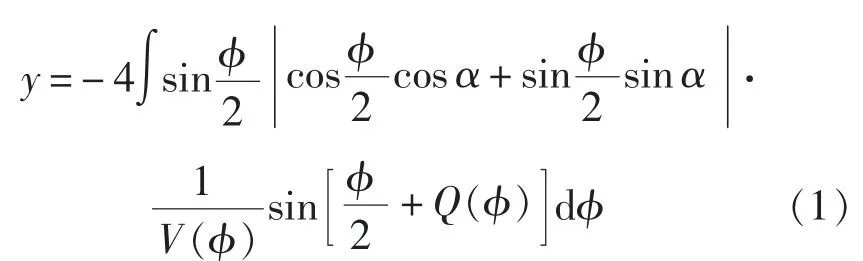
由于螺旋桨叶剖面一般都在较小的攻角下工作。当α较小时,可以认为cosα≈1,sinα≈α,根据式(1)可近似认为叶剖面的y坐标是近似与攻角α成正比的。因此,假定叶剖面的厚度t和拱度f与攻角之间存在如下关系:

式中,αu和αl分别是叶剖面上下表面对应的特征攻角,它们的选取和翼型剖面的几何特征直接相关。k1和k2是与攻角设置有关的比例系数。
3.1 叶剖面攻角设置
由于新的剖面设计方法要将攻角设置与剖面的几何参数联系起来,而叶剖面的参数,如厚度分布、拱度分布及设计升力系数由螺旋桨设计方法确定,因此,叶剖面的攻角设置必须能够反映叶剖面的几何特征,并且要能够对这些特征进行控制。因此,对翼型表面的攻角设置进行如图3所示的划分。
按照此种攻角设置,α2、α3、α5和α6用来控制叶剖面的厚度分布和拱度分布,α1和α7用来控制速度的收敛,α4用来控制导边吸力峰的出现。对应的极角设置如表1所示。

图3 叶剖面攻角设置Fig.3 Oistribution of angle of attack on airfoil

表1 极角设置(单位:度)Tab.1 Angle setting(°)
φ1和φ6分别用来控制翼型上下表面速度收敛区的长度。极角与长度之间可用下式进行转换:

以φ1为例,φ1等于66.42°、53.13°和36.87°,分别对应于上表面压力恢复的长度为0.3、0.2和0.1倍的弦长。较短的压力恢复长度可以有效地降低速度峰值,提高空泡起始速度;但过短的压力恢复会使得速度梯度过大而导致边界层流动分离。边界层分离会使得翼型升阻力性能发生急剧变化。因此,需要谨慎地选择压力恢复区的长度。φ4由Eppler设计程序迭代求解确定。
文献[5]研究表明,最大厚度靠近导缘的速度分布与最大拱度靠近尾缘的拱度分布相结合,有利于增大空泡斗的宽度。因此,为了增大翼型剖面的空泡斗宽度,设计的新剖面最大厚度应位于α3和α5对应的位置,而最大拱度应位于α2和α6对应的位置。根据式(2)则有如下关系:

假设α2所对应区域的最大厚度为t′而α3对应区域的最大拱度为f′,则有如下关系存在:

令t′=Cttmax,f′=Cffmax(Ct<1,Cf<1),则利用式(4)和(5)有

令α1=λ1α3,α7=λ2α3,α4=λ3α5,由于α4是用来控制导边吸力峰的出现,因此λ3应取大于1的值,一般可在1.5~2.5之间选取。λ1和λ2的值可根据需要由设计者灵活选取。
3.2 设计步骤
新的剖面设计主要有以下几个步骤:
1)选取参数λ1、λ2、λ3、Ct、Cf的值,并且确定α3、α5的初始值。α3、α5的初始值可以首先根据翼剖面的设计升力系数,确定一个初始的设计攻角αd,αd按照下面的关系确定:

式中,CL为设计升力系数;η为大于1的系数。确定了αd后,为了使空泡斗在设计升力系数附近有大致相同的宽度,可以令:

此时,根据式(4)和(8)则有

由式(9)可知,最大厚度与Δα成正比,因此Δα的初值可根据给定的厚度选取。
2)根据α3、α5的初始值和参数λ1、λ2、λ3、Ct、Cf的值,利用3.1节给出的方法确定其他的攻角及其对应的极角。
3)根据确定的极角和攻角分布,调用Eppler翼型设计程序进行翼型设计,并读取设计翼型的最大厚度x。
4)为了判断迭代设计过程是否收敛,引入以下误差函数:
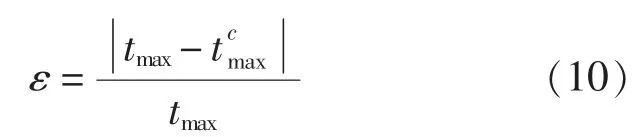
如果ε≤0.01,则认为迭代过程收敛,如果不收敛,根据tax和Δα的当前值和式(9)计算比例系数k1;根据给定的最大厚度tmax利用式(9)重新确定新的Δα。根据新的Δα返回第一步重新确定α3、α5和其他设计参数并重新设计,直到迭代过程收敛为止。
5)检查新剖面的空泡斗是否满足要求。如果不满足要求,则根据式(7)重新选择设计攻角αd,利用以上步骤重新进行设计直到空泡斗满足要求为止。
4 设计实例
利用本文提出的设计方法,分别设计了升力系数为0.2,厚度比为5%的翼型剖面E250和升力系数为0.3,厚度比为7%的翼型E370。它们各自的形状分别如图4和图5所示。

图4E370Fig.4 E370
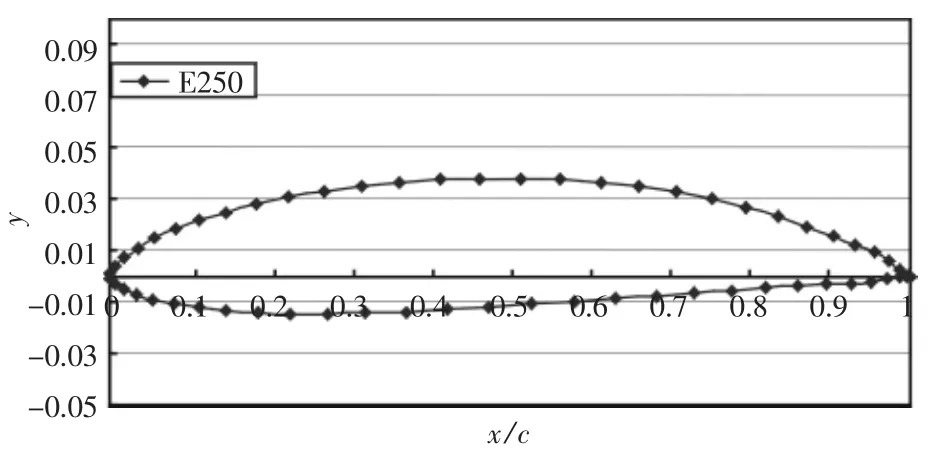
图5E250Fig.5 E250
翼型E370与翼型E250的拱度与厚度分布及其与NACA66mod+a=0.8剖面的对比,分别如图6和图7所示。
翼型E370与厚度比7%、设计升力系数0.3的NACA66mod+a=0.8剖面空泡斗对比如图8所示。翼型E250与厚度比5%、设计升力系数0.2的NACA66mod+a=0.8剖面空泡斗的对比如图9所示。

图6 拱度对比图Fig.6 Camber distribution

图7 厚度对比图Fig.7 Thinkness distribution

图8 E370与NACA66mod+a=0.8空泡斗对比Fig.8 Cavitation bucket of E370

图9 E250与NACA66mod+a=0.8空泡斗对比Fig.9 Cavitation bucket of E250
通过实例计算表明,本文所给出的设计方法对控制翼型剖面的厚度分布以及拱度分布是有效的。利用本文给出的设计方法,对翼型的拱度分布及厚度分布进行调整后,所得到新剖面的空泡斗在一定的空泡数范围内比NACA66mod+a=0.8要宽得多,抗空泡性能有明显的改善。
5 结论
本文在Eppler方法的基础上给出了一种根据指定的设计升力系数和厚度比进行翼型剖面设计的方法,并且建立了翼型表面攻角分布与厚度分布、拱度分布之间的联系,能够有效地控制翼型的厚度与拱度分布。本方法将翼型剖面设计与螺旋桨设计联系起来,设计出的新翼型剖面具有良好的抗空泡性能。但是翼型剖面设计是一项非常复杂的工作,在进行设计时有众多参数需要选择,设计者应综合各种设计指标,谨慎选择设计参数。
[1]RICHARD E.A Computer program for the design and analysis of low-speed airfoils[R].NASA-TM-80210,1980.
[2]RICHARD E.Direct calculation of airfoil from pressure distribution[R].NASA-TTF-15417,1974.
[3]SHEN Y T,EPPLER R.Wing section for hydrofoils-part 1:symmetrical profiles[J].Journal of Ship Research,1979,23:209-217.
[4]SHEN Y T,EPPLER R.Wing section for hydrofoils-part 2:nonsymmetrical profiles[J].Journal of Ship Research,1982,25:39-45.
[5]王大政,王言英.新型叶剖面设计及剖面参数对空泡特性的影响的研究—(2)剖面参数对空泡特性的影响[J].水动力学研究与进展(A辑),2000,15(3):319-328.
[6]华汉金.翼剖面优化理论在螺旋桨设计和减荷切削中的应用[J].船舶工程,2002(6):9-12.
[7]王国强,董世汤.船舶螺旋桨理论与应用[M].哈尔滨:哈尔滨工程大学出版社,2005.
[8]谭廷寿.非均匀流场中抗空泡桨叶剖面设计[J].船海工程,2006(3):1-5.
[9]王献孚.机翼理论[M].北京:人民交通出版社,1987.
[10]夏国泽.不可压缩边界层理论[M].武汉:华中理工大学出版社,1992.
A Design Method of New Anti-cavitation Airfoil Profile
Ge Liang1Long Wen2Xie Wei2Yang Xiang-hui2Qiu Liao-yuan2
1 Armament Procurement Agency,Naval Armament Department of PLAN,Beijing 100071,China 2 China Ship Development and Design Center,Wuhan 430064,China
A design method of new anti-cavitation airfoil profile based on Eppler design method was developed in this paper.This new design method was used for airfoil profile design with the specified thickness and lift coefficient.The relationships among camber distribution,thickness distribution and angle of attack were studied.An effective way which could control the position of cavitation bucket was also presented.The computation results demonstrate that the design method proposed is effective to control the thickness and camber distribution of profile.The cavitation performance of the new profile which was designed with the new method is better than that of the traditional airfoil profile.
airfoil profile;conformal mapping;cavatation
U664.33
:A
:1673-3185(2011)04-56-05
2010-09-07
戈 亮(1972-),男,硕士,工程师。研究方向:船舶工程。E-mail:glsl_2001@163.com
龙 文(1986-),男,硕士,工程师。研究方向:螺旋桨性能优化。E-mail:longwen304@163.com
谢 伟(1969-),男,研究员,博士生导师。研究方向:舰船总体性能优化
10.3969/j.issn.1673-3185.2011.04.011

