光滑互补函数与互补问题的 2-正则解

俞昊东 ,徐翠霞 ,濮定国

(1.同济大学应用数学系,上海 200092;2.河南科技大学数学与统计学院,河南洛阳 471003)

0 前言

讨论如下的非线性互补问题(记为NCP(F)):

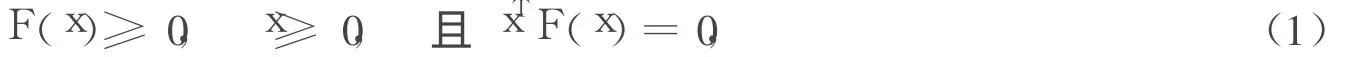
其中,x∈Rn,F:Rn→Rn是连续可微的非线性函数。对于互补问题的求解,最常用的求解途径是利用如下的互补函数将其转化为等价的非线性方程组。

定义1[1]对于二元函数φ:R2→R,若φ(a,b)=0当且仅当a≥0,b≥0,ab=0成立,则称φ是一个互补函数,或称NCP函数。

最基本的NCP函数是φmin(a,b)=min{a,b}。利用互补函数可构造如下方程组:

由NCP函数的定义易知,求解问题(1)等价于求解非线性方程组(2)。通常称(2)为再生方程组。利用非线性方程组求解互补问题的方法,可参见文献[1-2],求解非线性方程组全局解的方法可参见文献[3]。

设x*是问题(1)的一个解,若存在某指标i,使得=Fi(x*)=0,则称x*是一个退化解。否则,称x*是一个严格互补解,或非退化解。另一方面,对于再生方程组(2),若detφ′(x*)≠0(φ′(x)表示φ在x处的Jacobian阵),则称x*是方程组(2)的一个正则解。反之,若φ′(x*)奇异,则称它是一个奇异解。解的奇异性会给数值计算带来本质性的困难。例如,牛顿算法在奇异解的附近通常至多只能达到线性收敛性。

若互补函数φ是光滑的,则问题(1)的任一退化解x*必然是再生方程组(2)的一个奇异解。这种特性使得现今绝大多数求解互补问题的算法只能采用半光滑的互补函数,因而所得到的再生方程组通常也只能是半光滑的。半光滑算法方面的性质可参见文献[1,4-5]。2-正则性条件处理奇异解问题的重要途径,参见文献[6-7]。对于互补问题来说,由于再生方程组在奇异解处通常只能对 φ′求方向导数,而不存在二阶导数,因此文献[8-9]提出了一类只利用 φ′的方向导数的 2-正则性。其定义如下:

定义2[8]令x*是方程组(2)的一个解,设φ()在x*的某邻域内可微,且导函数φ′方向可微。令P是从Rn到零空间kerφ′(x*)的正交投影算子,且定义集合

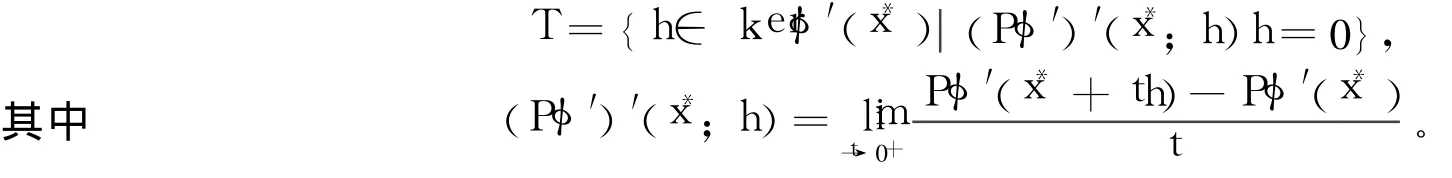
可以看出:若x*是(2)的正则解,则有kerφ′(x*)={0}。因此,x*必满足2-正则性。从而2-正则性是正则性的一种推广。这一概念的提出从理论上保证了可以设计出具有较好收敛性的光滑牛顿算法。

但对于 2-正则性的成立条件,已有文献仅对个别函数进行了讨论,如文献[8]研究了光滑互补函数φS(a,b)=2ab-{min(0,a+b)}2的性质,并证明了该函数,若x*使互补问题(1)满足b-正则性,则再生方程组在 x*成立 2-正则性。该文还对此结论的逆命题举出了反例。

本文将文献[8]的结果推广到一般情形,在分析光滑互补函数有关性质的基础上,证明了只要该类函数具有二次正齐次性及其他一些很弱的条件,b-正则性就能保证再生方程的 2-正则性,同时,对于 φS成立的反例对于一般的光滑互补函数也是有效的,从而给出了 b-正则性和 2-正则性关系的一般性结论。说明了对于在实际计算中可用的大多数光滑 NCP函数来说,2-正则性都是一个合理且容易满足的假设。

1 光滑NCP函数

光滑非线性互补函数有一些重要的性质。

引理1 设互补函数φ(a,b)光滑,即它是连续可微的。则有:①对任意的a≥0,=0;②对任意的b≥0,=0。

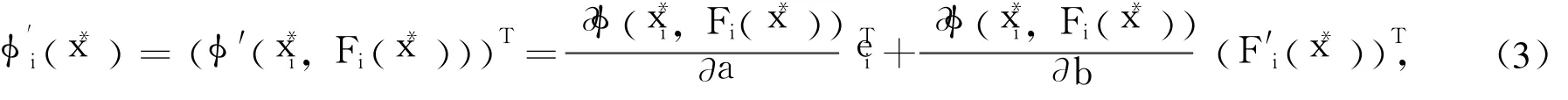
其中ei=(0,…,1,…,0)T(第i个分量为1)。则由引理1可得

因此,退化指标所对应的 φ′(x*)中的行向量等于0。由此立即得到以下结论。

引理2 若x*是问题(1)的退化解,则Jacobian阵φ′(x*)是奇异的。

2 二阶正齐次函数

对一般二元函数的二次正齐次性给出定义如下。

定义3 对于二元函数φ(a,b):R2→R,若对任意t≥0都有φ(ta,tb)=t2φ(a,b),则称函数φ(a,b)具有二次正齐次性。

特别注意到,若在上述定义中令 t=0,则有φ(0,0)=0。容易证明,具有二次正齐次的函数具有以下基本性质:

以下再给出此类函数的另一重要性质。

证明 若(x,y)=(0,0),由于φ(0,0)=0,等式显然成立。若(x,y)≠(0,0),不妨设x≠0。

(i)若x＞0,定义函数g1(s)∶=φ(1,s),s∈R。则由函数的二次正齐次性,φ(x,y)=x2φ(1,=x2g1()。因此,

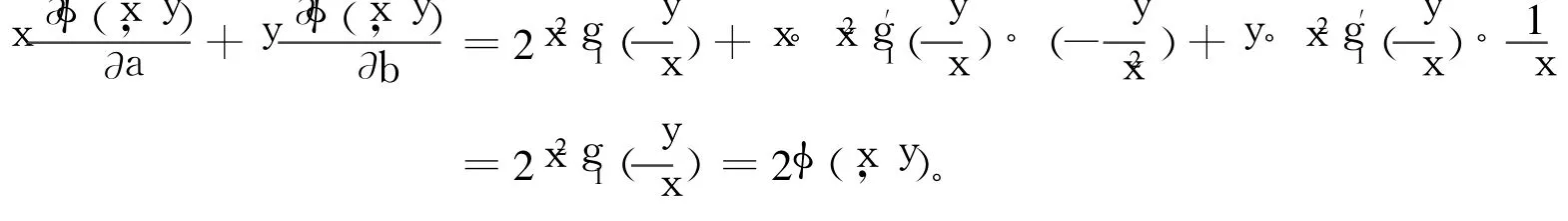
(ii)若x＜0,定义g2(s)∶=φ(-1,s),(s∈R)。由函数的二次正齐次性,φ(x,y)=x2g2(-)。同上可证得),故等式仍然成立。由上述(i)、(ii),命题成立。证毕。

分片线性的或一次的互补函数通常至多是半光滑的,因而光滑的互补函数一般至少是二次的。另一方面,若采用的互补函数次数过高,又会大大增加再生方程组的非线性化程度,给数值求解带来困难。因而,对于实际算法中可用的大多数光滑互补函数来说,二次正齐次性是合理而基本的假设。

3 b-正则性与2-正则性

首先给出 b-正则性的定义如下,b-正则解的相关性质可参见文献[1,5]。

定义4[1]设x*是互补问题(1)的一个解,记G=F′(x*),若对任意子集α⊆δ⊆α∪β,主子阵 Gδδ非奇异,则称 x*是互补问题的一个b-正则解。

容易看出,x*是b-正则解等价于以下条件成立:对集合β的任意剖分(A,B),即A∪B=β,A∩B=Ø及h∈Rn,都有

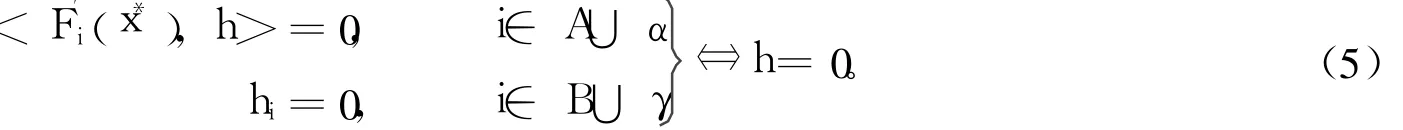
为讨论b-正则解和2-正则性的关系,需对光滑互补函数φ(a,b)作如下假定:(A1)φ是二次正齐次函数;(A2)≠0且≠0;(A3)导函数φ′方向可微(但一般不能假定可微)。

定理1 设x*是互补问题的一个b-正则解,若互补函数φ(a,b)是光滑的且满足假设(A1)～(A3),则由此得到的再生方程组(2)在 x*满足2-正则性。

证明 由于互补函数φ是光滑的且满足假设(A3),且函数F(x)连续可微,易知φ′方向可微。由投影算子P的定义,若存在h∈Rn使(Pφ′)′(x*;h)h=0,则(φ′)′(x*;h)h∈imφ′(x*),其中, imφ′(x*)表示φ′(x*)的象空间。则由式(4)可得,对所有i∈β,都成立(φ)′(x*;h)h=0。故得T⊆T1∶={h∈kerφ′(x*)|(φ)′(x*;h)h=0,∀i∈β}。因此,要证明2-正则性,只需证明T1={0}。任取i∈β,由式(3)及式(4),φ(x*)=0,且对任意h∈Rn及t＞0有φ(x*+th)=(F(x*+th))T。由Fi(x*)=0,得=＜F(x*),h＞。又显然有F′i(x*+th)=(x*),故由引理3可知:

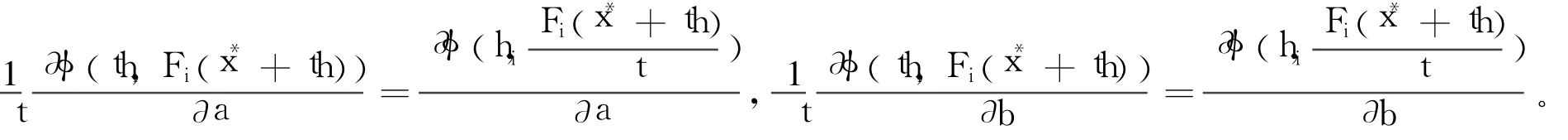
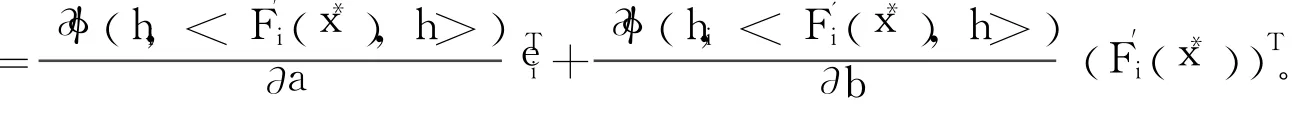
则由引理4可得:

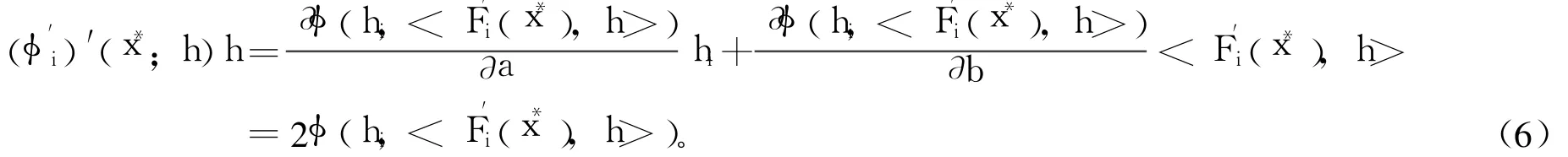
容易验证,若条件(5)成立,则式(7)必成立,因此再生方程组(2)在x*成立2-正则性。证毕。

4 讨论

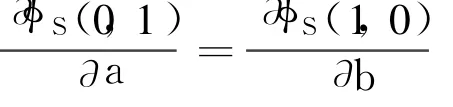
还可以新定义一类互补函数φM(a,b)=(a+b)-(a2+b2),显然它也是二次正齐次的,并且

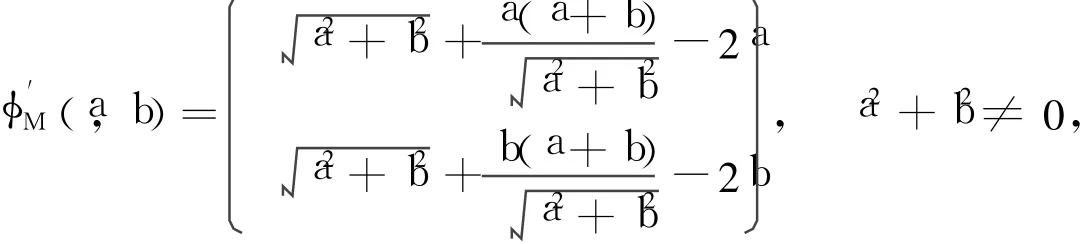
最后讨论定理1的逆命题,即若x*是再生方程组(2)的2-正则解,它是否是互补问题的b-正则解。文献[8]对于互补函数 φS举出了如下反例。

例1 在互补问题(1)中,令n=2,F(x)=(x1,-(x2-ρ)2)T,x∈R2,其中ρ＞0。该问题的唯一解是x*=(0,ρ)T。这是一个退化解,且β={1},α={2},γ=Ø。由条件(5)易知:b-正则性在x*不成立。

文献[8]对 φS验证了 x*是方程组(2)的 2-正则解。因此对于函数 φS来说,例 1构成了一个反例。这里给出对一般情形的讨论,即对例 1有如下命题。

命题1 若互补函数φ是光滑的且满足假设(A1)～(A3),且下列极限存在

则例1所对应的再生方程组在x*有2-正则性。

证明 计算可得,φ′(x*)=0,故kerφ′(x*)=R2,从而投影矩阵P=I。由β={1}及式(6)易知:对任意h∈R2,(φ)′(x*;h)h=2φ(h1,h1)。因此,由()′(x*;h)h=0可知h1=0。

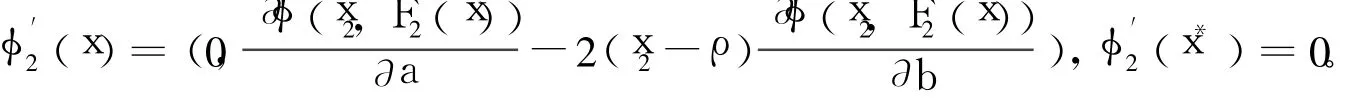
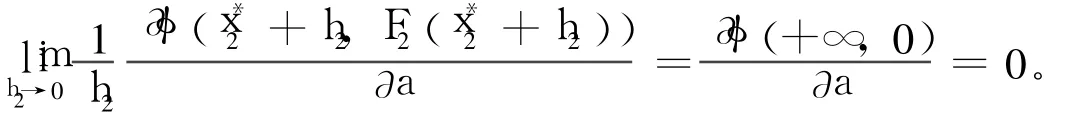
因此h=0,亦即T={0},从而x*是2-正则解。证毕。

命题1表明:例1对于满足(A1)～(A3)且极限(8)存在的一大类光滑互补函数都是一个反例。容易验证,φS和本文新提出的φM都符合命题 1的条件。因而,在一般意义上,2-正则性严格地弱于 b-正则性。

[1] 韩继业,修乃华,戚厚铎.非线性互补理论与算法[M].上海:上海科学技术出版社,2006.

[2] 陈小君,张超.非线性方程组在几类计算问题中的应用[J].长沙理工大学学报:自然科学版,2006,3(4):1-7.

[3] 尚有林,杨森,王三良.无约束全局优化的一个新凸填充函数[J].河南科技大学学报:自然科学版,2004,25(3):92-95.

[4] 濮定国,王华.集映射算子和半光滑性[J].同济大学学报:自然科学版,2008,36(9):1278-1281.

[5] Facchinei F,Pang JS.Finite-dimensional Variational Inequalities and Comp lementarity Problems:Vol Iand Vol II[M].New York:Springer,2003.

[6]Oberlin C,W right S.An Accelerated Newton Method for Equations with Semismooth Jacobians and Nonlinear Complementarity Problems[J].Math Program:Ser B,2009,117:355-386.

[7] Griewank A.On Solving Nonlinear Equations with Simple Singularities or Nearly Singular Solutions[J].SIAM Rev,1985, 27(4):537-563.

[8] Izmailov A,Solodov M.Error Bounds for 2-regular Mappings with Lipschitzian Derivatives and their App lications[J].Math Program,2001,89(3):413-435.

[9] Daryina A,Izmailov A,Solodov M.AClass of Active-set New ton Methods forMixed Complementarity Problems[J].SIAM J Optim,2004,15(2):409-429.