水动推进力及其应用
陈振诚 陈昕 陈旸
(中国科学院国家天文台流体力学小组 北京 100012)
水动推进力及其应用
陈振诚 陈昕 陈旸
(中国科学院国家天文台流体力学小组 北京 100012)
流体动力学;水动力学;水动推进力;水动升力;涌浪导流槽
考虑到三维效应和重力影响,提出研究设置导流槽的船底在水面滑行激起的流场以及作用在槽和船底浸湿面上的水动力。该导流槽的顶部曲面前低后高,对船底基面形成倾角。运用严谨的数学物理方法解决问题,求得描绘三维流场状况的解析函数,由此获得船艇前进时出现在槽顶部曲面上推船艇前进的水动推进力和向上的水动升力定量值的解析表述式。将船底浸湿面设计成设置导流槽的外形,建成实船试航,通过卫星跟踪的GPS系统实测获得的数据证明了水动推进力的存在,且它随着航速的提高而迅速增大,于是船速以及稳定性、安全性均得以大幅提高。实船设计时,可通过合理调整表述式中的物理参数,设计建造整体性能远优于常规船艇的实船。
0 引言
常规船艇在纵向基面对水平的攻角θ=0时前进,水动升力L0=0,船的总重量由等于排水量的水浮力承担,这种船称为排水型船。每条尺度不同的船都有各自无法超越的水的阻力峰。例如船长约150m,排水量约6 000 t,吃水深度约6m的常规驱逐舰或巡洋舰,推进功率约10万马力,航速只能达到约30 kn。船长约400m,排水量约10万吨,吃水深度约11m,推进功率约28万马力的航空母舰,航速只能达到约33 kn。如果对它们再加大推进功率,航速不会相应地提高,其根本原因就是它们没有能力克服水的阻力峰。排水型的集装箱船、滚装船都是这样,想提高其航速,十分困难。
为了使船行驶时能激起人们所期望的水动力,并以此来克服水的阻力峰,从而提高其航速以及整体性能,我们考虑设置特殊的船底浸湿面的外形,也就是在船底浸湿面的纵向设置一条、两条或多条涌浪导流槽,槽的顶部曲面在纵向前低后高,对船底基面形成倾角α,α大于纵向船底基面对水平面的攻角θ。在两船舷设置压浪阻溅流挡板,挡板的顶部曲面也是前低后高,对船底基面形成倾角α。导流槽向前、向后、向下敞开,挡板向前、向下、向后、侧向向外敞开。导流槽和挡板的顶部横剖面都是圆弧形。
在船底浸湿面设置对称平行于船底纵向中心线的一对导流槽,以及在两船舷设置压浪阻溅流挡板的情况下,当船前进时,船艏附近部分水流进入导流槽和压浪挡板,从而降低了船艏附近和两船舷外侧的水面涌高,降低了水阻力。在船底下面的水流受前进船底的推压,从侧向挤入导流槽和压浪挡板,会合从前方进入的水流,一同被导向艉部并顺畅地流出船尾。于是对槽和挡板纵向前低后高的顶部曲面形成足够强大的法向压力,其水平分量的方向与船行方向一致,推船前进,即为名符其实的水动推进力,其垂向分量即为水动升力。它们迫使船艇航速大幅度提高,稳定安全性大幅度增强。文中我们对前人的水动升力近似估算方法[1]做了讨论。
为了理论分析时的简要、清晰,在下一节中先考虑设置一条导流槽。
1 设置一条导流槽的水动力流场和相应的水动力
假定在半无限空间-∞≤x≤∞,-∞≤y≤0,-∞≤z≤∞,域中被水充满,水的密度ρ=常数。假定长度2a、宽度2b、槽宽为2l、吃水深度为δ的船底浸湿面,以攻角θ、速度U在水面滑行,槽顶部曲面对船底基面形成倾角α(α>θ),见图1。置坐标原点于船底纵向中心线和横向中心线的交点处。
图1中:x、y、z为坐标系,O为坐标原点,θ为船底纵向基面对水平面的攻角,α为导流槽的顶线对船底基面的倾角(α>θ),2a为船底浸湿面的长度,2b为船底浸湿面的宽度,2l为导流槽横剖面的宽度,h′为导流槽末端的高度,h为水动推进力作用点的吃水深度,L为作用在导流槽顶部曲面上的水动升力,P为作用在导流槽顶部曲面上的水动推进力。L0为作用在槽外两侧浸湿面上的水动升力,R0为作用在槽外两侧浸湿面上的水动阻力。
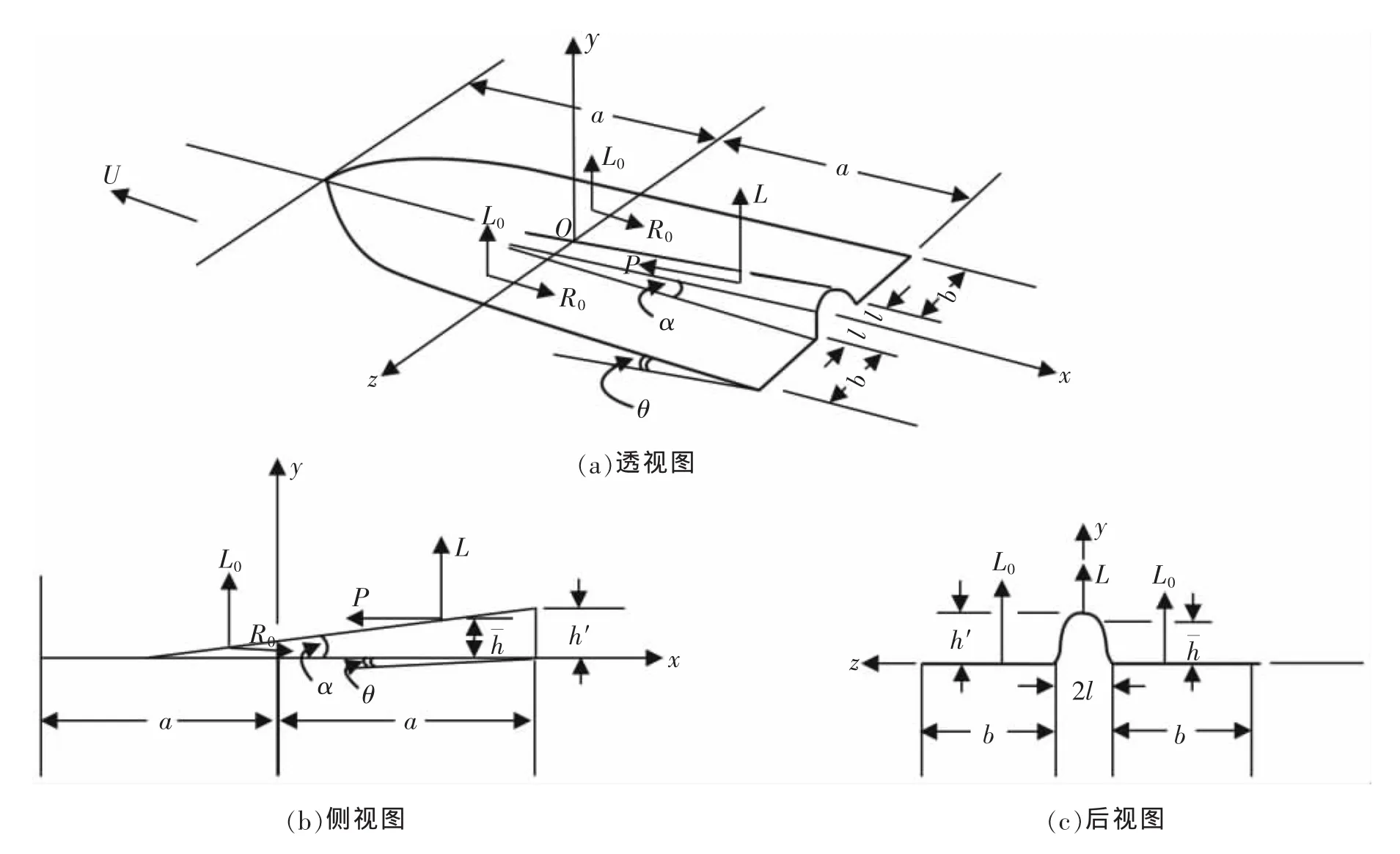
图1 在船底纵向中心线设置导流槽的船底浸湿面直线前进时的示意图
水的运动可以用流体速度势函数Φ(x,y,z)=Ux+φ(x,y,z)表述。其中φ(x,y,z)是被扰动流体速度势函数,U是船底浸湿面的滑行速度。
流体速度势函数满足下列的偏微分方程,它是连续方程

我们定义在空间域-∞≤x≤∞,-∞≤y≤0,-∞≤z≤∞中被水充满,此处Φ(x,y,z)≡Φ(x,y,z),但是在域-∞≤x≤∞,0<y≤∞,-∞≤z≤∞中没有水,此处Φ(x,y,z)≡0。
假定在水自由表面-∞≤x≤∞,y=0,-∞≤z≤∞处为大气压力。于是,我们可以导出水自由表面的边界条件如下式[6]

假定,在浸湿面的远前方,流体的被扰动趋向于0,也就是说,在x→-∞处;
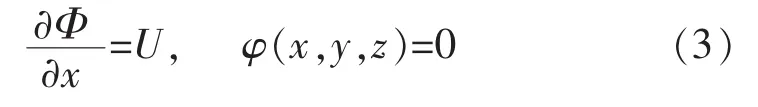
在浸湿面的远左方或远右方,流体的被扰动趋向于0,也就是说在z→∞或z→-∞处;

在y→-∞处;

在船底浸湿面上的边界条件,也就是说在-a≤x≤a,y=-δ,-b-l≤z≤b+l面上

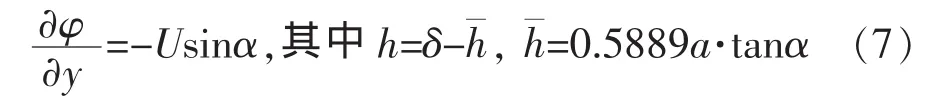
在导流槽顶部浸湿面上,也就是说在-a≤x≤a,y=-h,-l≤z≤l面上,在导流槽两边垂向壁面上,也就是在-a≤x≤a,-δ≤y≤-(δ-h′),|z|=l面上,

在船底浸湿面的尾端,也就是在x=a处,水流顺畅地流出浸湿面的尾端,也就是说,此处水流的速度为有限值,

在x→∞处流体的被扰动速度为有限值,也就是

现在我们已经建立上述合理的物理模型和描述该模型的系列偏微分方程。在下节中我们将用严谨的数学物理方法解出那些方程,从而获得问题的唯一解析解。
2 求解方程,确定流体速度势函数
依据上节中所述的物理模型,寻找问题的解就归结为找到分别能满足上节中方程(1)和边界条件(2)~(10)的流体速度势函数Φ(x,y,z)。
我们采用一种积分变换[7-9]解决问题。
满足方程(1),得到Φ(x,y,z)=Ux+φ(x,y,z),此处

假定:a是参考长度;而x′=x/a,y′=y/a,z′=z/a,b′=b/a,δ′=δ/a,a′=a/a=1。为了便于书写,可以把x′,y′,z′,b′,δ′写成x,y,z,b,δ。
把式(11)代入式(6),滑行船底浸湿面上的边界条件被满足,于是我们得到

把式(11)代入式(7),导流槽顶部浸湿面上的边界条件被满足,

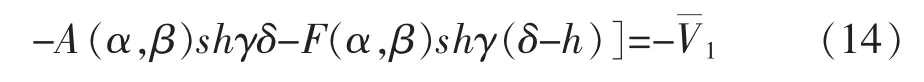
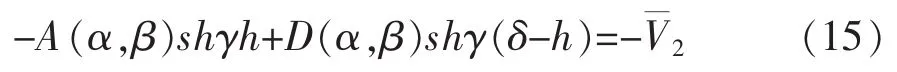
式中:

此处λ0=α-c0,λ1=β+c1,δ>h,h是在导流槽顶部曲面上P和L的作用点的吃水深度。
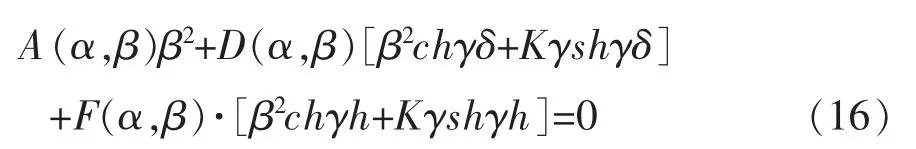
把式(11)代入式(2),水自由表面的边界条件被满足。我们得到由于γδ、γh为小量,可以视chγδ=1,chγh=1,shγδ=γδ,shγh=γh;于是式(16)可简化为

式中:Q=β2+k0γ2,R=β2+k3γ2,k0=Kδ,k3=Kh。解联立方程(14),(15),(17)可以得到
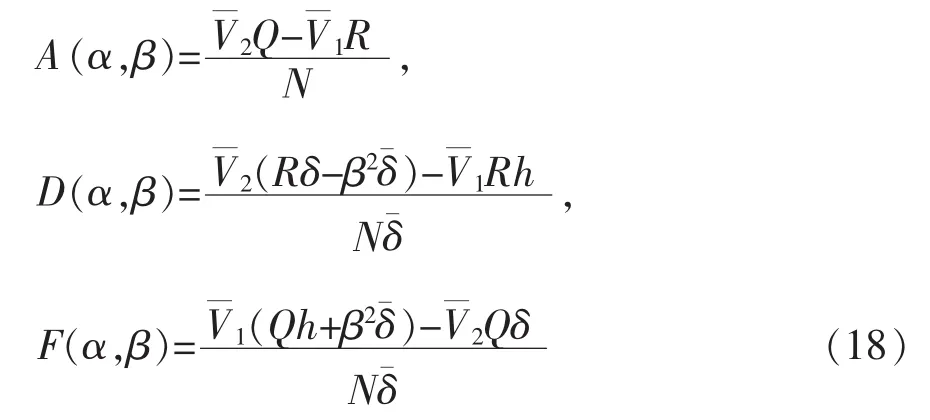
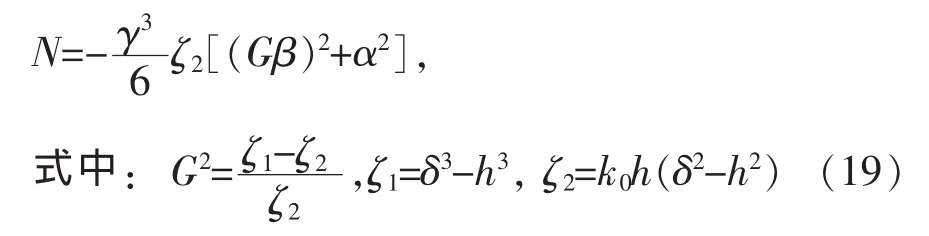
到此,式(11)中的任意复变函数A(α,β),D(α,β),F(α,β)已被确定。
把式(18)代入式(11),条件8被满足。沿指出的积分环路进行积分运算[7-9],可以证明边界条件(3),(4),(5),(9),(10)都能满足。现在我们已经确定式(11)中φ(x,y,z)能满足本问题所有的边界条件和方程,也就是说,本文所提问题的唯一解析解已经被找到。φ(x,y,z)是能够描述三维被扰动流场的流体速度势函数。
3 证明解的唯一性
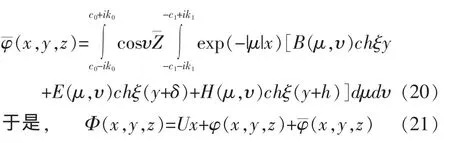

在y=-h处,
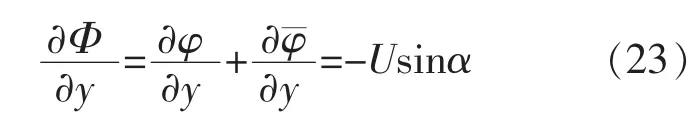
分别把式(6)代入式(22),把式(7)代入式(23),则有

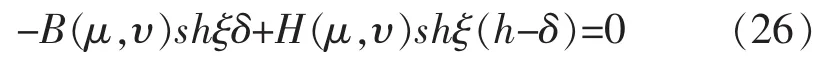
由式(25)导出,在-a≤x≤a,y=-h,-l≤z≤l面上也就是
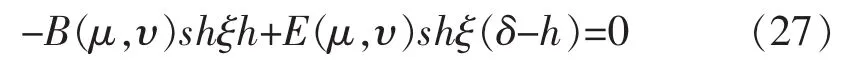
把式(21)代入式(2)以满足水的自由表面的边界条件,我们得到
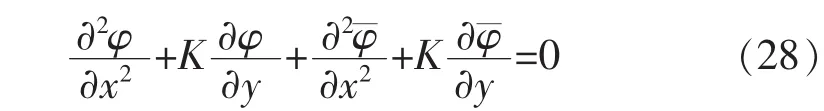

解联立方程(26)、(27)、(29),得B(μ,υ)=0,E(μ,υ)=0,H(μ,υ)=0。把它们代入式(20),我们得到

所以问题的解只能是

可见,在上节中找到的Φ(x,y,z)=Ux+φ(x,y,z)是这个问题的唯一解。本证明成立。
4 寻求作用在船底浸湿面上的水动力
船前进时,
1)作用在导流槽顶部曲面-a≤x≤a,y=-h,-l≤z≤l上的法向水动压力为

从式(11)可导出,此处


图2 在复平面α上的积分回路

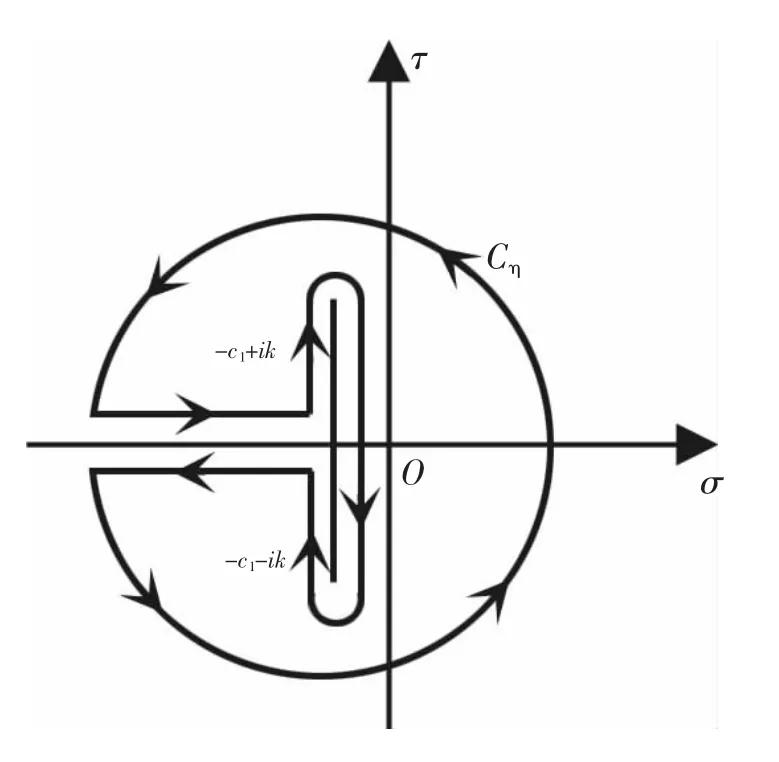
图3 在复平面β上的积分回路

所以作用在导流槽顶部曲面上,吃水深度-h处的水动推进力P=Nasinα,

可参见图1中的透视图、侧视图、后视图上标出的P,L。
2)作用在导流槽外两侧浸湿面-a≤x≤a,y=-δ,-l-b≤z≤b+l上的水动压力为
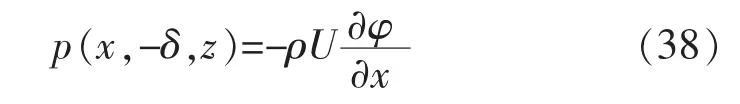
从式(11)可导出,此处的


从而求得法向水动力,

于是求得作用在导流槽外两侧浸湿面上的水动升力L0=N0cosθ,

可参见图1中的透视图、侧视图、后视图上标出的L0,R0。
由于在动态情况下,故很难确切测定在运动中不断变化的攻角θ与吃水深度δ。因此,引入修正系数η(0<η≤1),把式(37)、(42)改写成
作用在导流槽顶部曲面上的水动推进力
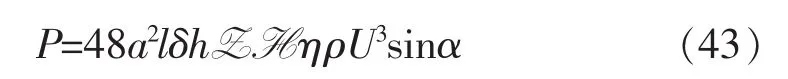
而水动升力为

作用在导流槽外两侧浸湿面上的水动升力
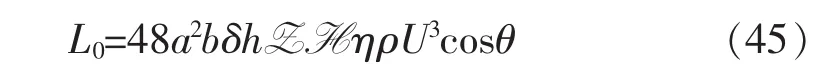
而水动阻力为

修正系数η可以根据实际情况用实验确定之。或者用L+L0=W,W为期盼得到的水动升力。例如:对于小艇,W=艇的总重量,这时艇进入滑行航态;对于中、大型船艇,W=部分船艇总重,这时船艇在部分滑行航态。α为设计倾角,θ为滑行攻角,δ为船底浸湿面的吃水深度,U为船底浸湿面的滑行速度。
到此,船前进时激起的水动推进力P,水动升力L,L0,水动阻力R0的定量值解析表达式已被找到,如式(43)~(46)所示。它们分别是船底浸湿面对水平面的攻角θ,导流槽的顶部曲面对船底基面的倾角α,船运动速度U,体现重力场对流场作用的重力加速度g,船底浸湿面的长度a,宽度b,导流槽的宽度l,导流槽顶部曲面上P,L作用点的吃水深度h,船底浸湿面的吃水深度δ,水的密度ρ的函数。这充分体现了本文研究得到的结果,具有严谨的数学物理基础。
在下节,我们将阐述依据上述各力的合理分布,设计建造实船。在实航中卫星跟踪的GPS系统实测得到的准确数据与上列(43)~(46)各式得到的理论数据相对比,从而证实理论与客观实际相符合。
(未完待续)
[1]姜次平,邵世明.船舶阻力,升力系数[M].交通大学出版社,1985,P.202,216.
[2]Jacob W.R,Tsakonas.S.A,New procedure for solution of lifting surfare problems[T].Journal of hydronautics,1969.3(1).
[3]Courant R.Hillert D.Me the matical physics,Volume 2,partial Differential Equations[M].Interscience publishers,John wiley&sons,1962.
[4]Robinson A,Laurmann JA.Wing Theory[M],University press Cambridge,1956.
[5]Milne-Thomsom L M.Theoretical Hydrodynamics(4th Edition)[M].
[6]朱蔚文,张涤明.水动力学[M].高等教育出版社,1993,P.17.
[7]Chen Zhen-cheng.A method to solve Boundary Value problem[J].Kexue Tongbao,Vol.26.No.1,1981,P.16-23.
[8]Chen Zhen-cheng and Chen Yang.Solar Force-free Magnetic fields on and above the Photosphere[J].Appendix,An Integral Transform,Solar Physics,1989,P.294-299.
[9]陈振诚.解决流体动力学某些问题的积分变换[C].第十二届全国水动力学研讨会论文集.1998.9.
[10]Chen Zhen-cheng,The hydrodynamic pressure on sluice gate plane wetted by water in the case of free outflow[C].Proceedings of the Second Asian congress of Fluid Mechanics,Science press,Beijing China,1983,P.555-557.
[11]Chen Zhen-cheng.The hydrodynamic pressure on sluice gate plane wetted by water in the case of submerged outflow[C].Proceedings of the Third Asian congress of Fluid Mechanics,Tokyo,Japan,1986,P.142-145.
[12]Chen Zhen-cheng,The criterion for presaging occurrence of solar flare[C].Proceedings of the Fifth Asian congress of Fluid Mechanics,Taejon Korea,1992,P.920-923.
[13]Sneddon,I.N.Fourier Transform,N.Y.Graw 1951.
[14]朱珉虎.飞鳐水面航行器[J].船舶,2002,6(3).
[15]陈振诚,陈昕.激起水动推进力的新船型[J].国际船艇,2005,9(5).
[16]陈振诚,陈旸.水动力矩助船艇回转且抗倾覆[J].国际船艇,2006,2(1).
[17]陈振诚,陈昕,陈旸.一种崭新的船舶运行原理[J].船舶工程,2006,8(4).
[18]Chen Zhen-cheng.Planing Vessel[C].Bulletin of International.Bureau ofWIPO,Feb.1996.
Hydrodynamic propulsion and its application
Chen Zhencheng Chen Xin Chen Yang
hydrokinetics;hydrodynamic;hydrodynamic propulsive force;hydrodynamic lift;swell blast groove
Taking account of the 3-D effect and the gravity impact,this paper studies the flow field which has been activated when the ship bottom with blast groove slides on the water surface and the hydrodynamic of the wetted surface of the ship bottom.The top curved surface of the blast groove is higher in fore and is lower in aft,which forms an obliquity against the bottom baseplane.The rigorous methods in mathematical physics are applied to work out the analytic function describing the 3-D flow field in order to obtain the hydrodynamic propulsive force,which appears on the top curved surface of the groove when the ship moves forward,and the quantificational analytic expression for the hydrodynamic lift.The wetted surface of the ship bottom is designed to be able to set blast groove,and the ship trails are build to prove the existences of the hydrodynamic propulsive force through the data obtaining from the satellite tracking GPS system.It augments rapidly along with the increasing ship speed,so the ship speed,stability and security all are improved greatly.In terms of the ship design,the overall design and construct performance surpasses the regular ship by rationally adjusting the physical parameters in the expressions.
U661.1
A
1001-9855(2011)01-0010-06
2010-10-29
陈振诚(1929-),男,汉族,中国科学院研究员。主要从事舰船水动力学,跨科学从事电磁流体力学(太阳磁场、黑子、耀斑)等课题的研究工作。
陈昕(1972-),女,汉族,高级工程师,主要从事计算机软件研究工作。
陈旸(1962-),男,汉族,高级工程师,主要从事船舶动力学研究工作。
一种积分变换[7-9],从上列两式分别得到相应的下列两式,

