基于复合控制的单相光伏逆变电源的研究

陈圆圆， 卢秀和， 薛 鹏， 马金婷

(长春工业大学电气与电子工程学院，吉林长春 130012)

0 引 言

随着不可再生能源的减少，人们不断加大力度开发新型可再生能源。其中，太阳能凭借其独特的优势成为众多可再生能源的焦点。光伏发电系统框图如图1所示。

图1 光伏发电系统

从图中可以看出，光伏发电系统包括太阳能电池板阵列、充放电控制器、蓄电池和逆变电源4部分。其中逆变电源是关键部件。基于光伏系统对逆变电源有较高的逆变效率和输出失真度小的要求，因此，对光伏逆变电源控制方法的研究非常重要。在光伏逆变电源系统中常采用的数字控制方法是PID控制，但是PID控制稳态性能不佳，使输出误差较大。因此，文中拟采用PID控制和重复控制相结合的复合控制，以增加系统的稳态性能。

1 逆变器系统结构和数学模型的确定

逆变器从主电路结构上分为单级变换和双级变换结构。单级变换结构虽然简单，但是需要较高的直流输入，而光伏阵列输出不稳定，并且在不同光强和温度条件下，直流母线电压变化范围大，影响系统的输出性能，因此，光伏逆变电源不宜采用此种变换结构。双级变换结构不仅可以通过调节DC/DC变换器的占空比完成光伏阵列的最大功率跟踪，还可以稳定的向DC/AC输入直流电压，而DC/AC则可以实现并网和给交流负载供电。两种变换结构如图2和图3所示。

图2 单级独立变换逆变器结构图

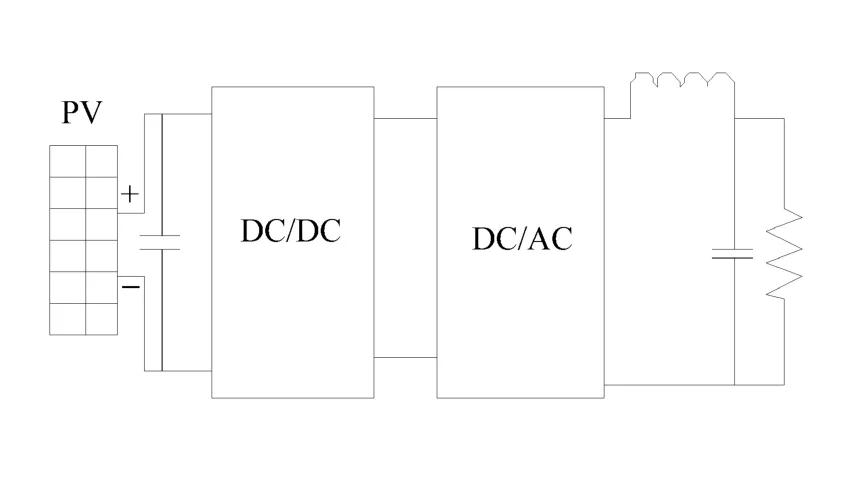
图3 双级独立变换逆变器结构图

文中采用双级变换结构。在本系统中利用DC/DC变换器把太阳能电池板的输出电压变换成稳定的直流电压，然后作为逆变器的输入。文中的DC/DC环节设置为输入电压范围大，有较高的转换效率的Boost电路;DC/AC设置为全桥逆变电路，主电路拓扑结构如图4所示。

图4 光伏独立逆变结构简图

根据上面的两级结构建立逆变器中DC/AC部分的数学模型。带滤波电感、电容的单相光伏逆变器的电路如图5所示。

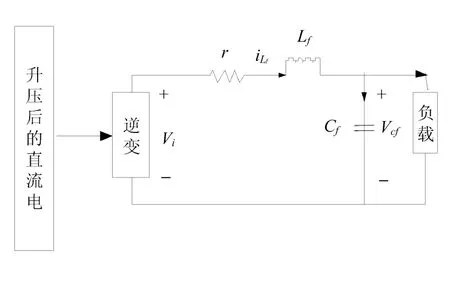
图5 单相光伏逆变器电路

图中:Vi——逆变桥输入电压;

r——滤波电感L f等效电阻;

L f——滤波电感;

Cf——滤波电容;

Vcf——电容电压;

iLf——滤波电感电流;

i0——负载上的电流。

因为滤波电容等效电阻很小，常常予以忽略。

把Vi和i0看作系统的两个输入量，Vcf作为系统输出，得到逆变器的状态空间表达式如下所示:

式中:

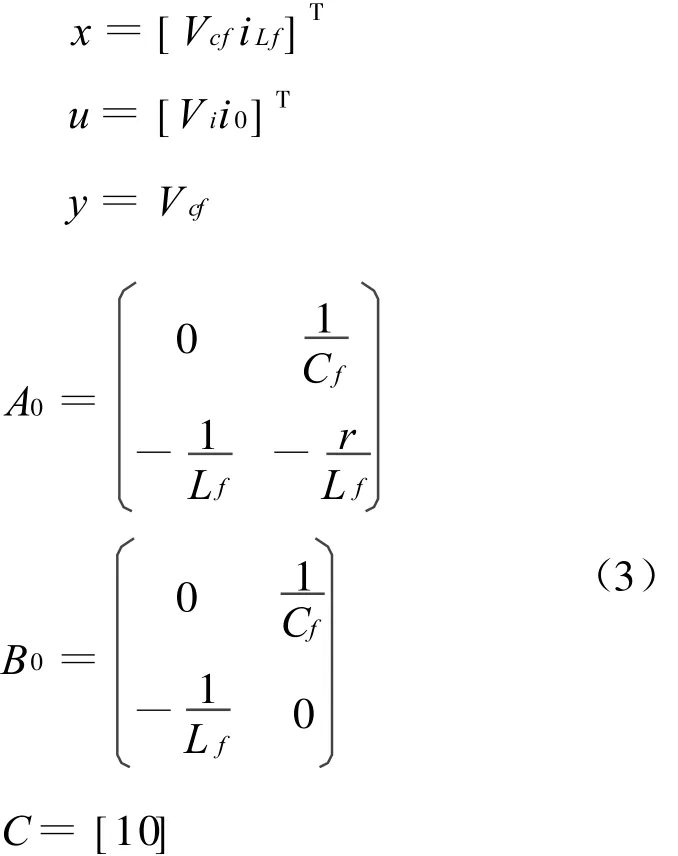
由状态方程进一步可以得到当Vi和i0同时作用时，系统的S域输出响应表达式为:

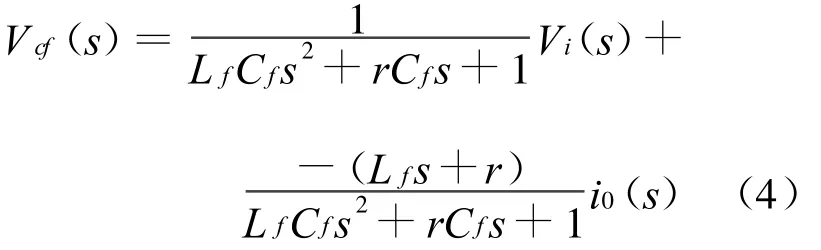
设负载为阻性负载，阻值为R，可得到逆变器数学表达式P(s)为:

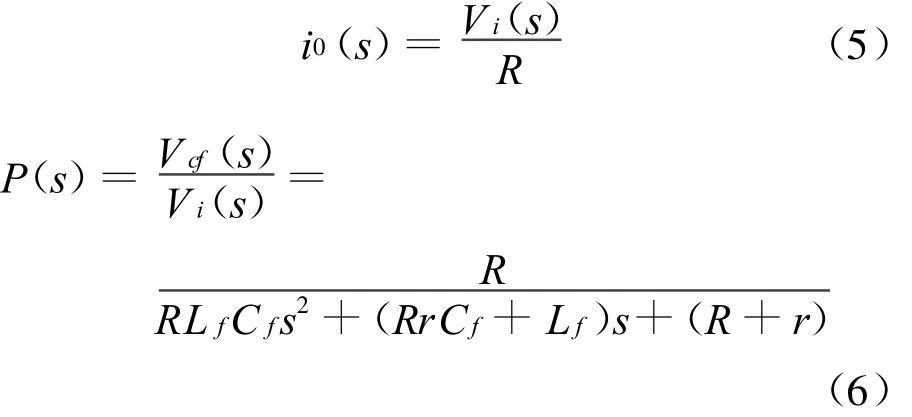
从上面可以看到，这是一个双入单出的二阶线性系统。逆变桥输出电压Vi作为控制量输入，负载电流i0则可以认为是扰动输入。逆变器所接负载类型很有可能是非线性的，但是这种非线性仅仅体现在扰动量的任意性上，逆变器模型仍然是一个简单的二阶线性模型[1]。这样做实际上是把负载电流处理为一种可测扰动。

文中采用的是数字控制方法，下面来推导此种结构逆变器的离散模型。在采样过程中把变量在采样时刻的瞬时值作为其在此周期内的采样值。这样由式(1)和式(2)导出其离散模型。

式(9)则由式(3)推出，从而得到逆变电源P(z)的离散数学表达式。

式中:Ta——采样时间。

系统中取采样频率等于开关频率，根据冲量等效原则，让逆变桥输出电压每个周期的平均值等于采样值。

2 复合控制策略的研究

重复控制是一种基于内模原理的控制策略。重复控制方案把作用于系统外部信号的动力学模型植入控制器，从而构成高精度反馈控制的设计原理[2]。从内模原理可以知道，只有对每一个扰动设置一个正弦波内模，才能使系统的输出无静差。但是这种结构非常复杂，在实际中很难实现并应用。重复控制通过植入重复信号发生器G(z)=1/(1-Z-N)，解决了这个难题[3]。它的控制思想为假定上一个周期输出的电压波形的畸变将在下一个周期的同时刻出现，控制器通过计算给定指令和反馈信号的误差来确定校正信号，并将此校正信号加在原控制信号上以消除输出电压的畸变。即使当输入信号为零时，重复控制器还是会不停地累加，不断输出累加0，从而保持输出波形稳定。

重复控制系统的结构如图6所示。

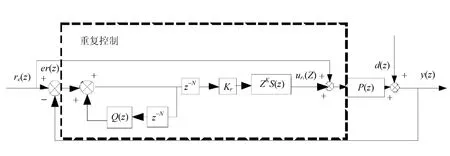
图6 重复控制系统结构

图中:y(z)——输出信号;

re(z)——参考信号;

er(z)——误差信号;

d(z)——重复性扰动信号;

Z-N——周期延时环节;

ZK——超前环节;

S(z)——补偿器;

Q(z)——滤波器;

P(z)——被控对象，在这里为逆变器数学模型。

当er(z)不为0时，重复控制器逐周期地累加，控制器不断修正输出波形，当er(z)为0时，不断输出上一周期的波形，这时输出稳定。

由图6可得重复控制器输入、输出关系表达式:

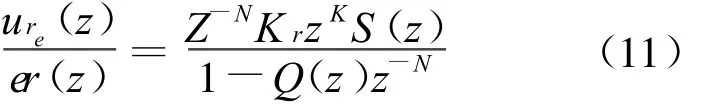
还可以得到误差er(z)的表达式:

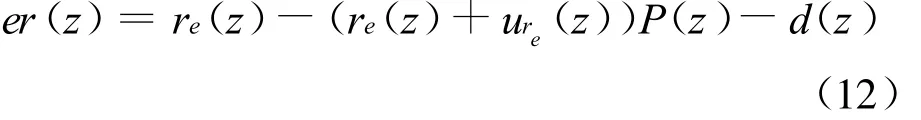
由式(11)和式(12)得到误差re(z)与d(z)两者之间的关系式:

由式(13)可得其特征方程:

根据控制理论中的小增益原理得到系统稳定的充分条件:

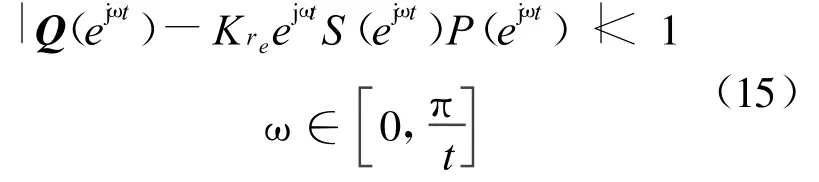
由式(15)可知，ω从0～∞的变化过程中，矢量KreejωtS(ejωt)P(ejωt)的末端所划过的轨迹不能超出以矢量Q(ejωt)的末端为圆心的单位圆。所以如果想让系统稳定，要使Q(z)＜1。

重复控制虽然具有较高的跟踪精度，但是从图6可以看出，它的控制指令不是马上输出的[4]。而是有一个输出的延迟，这就预示着在被扰动后的一个周期里重复控制器对扰动信号没有任何的抑制作用，系统相当于是一个开环，稳定性很差，在遇到大的干扰信号时，很可能使电压输出大范围的升降，进而损坏用电设备[5]。而数字PID控制对跟踪误差能够马上调节，但是其控制精度差，输出波形畸变严重，基于重复控制有良好的稳态性，而PID控制具有良好的动态性能，将两者结合起来组成一种复合控制，使系统具有较好的动态性能和稳态性能。

基于PID控制和重复控制的复合控制框图如图7所示。

图7 复合控制系统结构

该方案中，重复控制和PID控制并联在前向通道上，当系统跟踪误差小时，重复控制起作用;当系统出现大的扰动，重复控制由于其有一个周期的延迟，不产生作用，但是PID控制能够马上感知扰动并立即产生调节[6]。一个周期后重复控制器的调节作用使跟踪误差变小，当误差小到一定程度时，PID控制器调节作用减小至0，重复控制继续调解直到系统重新处于稳定运行状态。

DC/DC变换电路，采用文献[7-8]提出的改进的单周控制策略，将光伏电池板输出的不稳定的直流电压转换为稳定的直流电压400 V。通过以上分析，将整个系统控制框图给出，如图8所示。

图8 系统控制结构

3 仿真研究

根据以上分析，文中对数字PID控制、复合控制进行了仿真研究。DC/DC输出为直流

DC/AC输出电压为

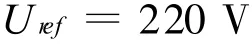
输出电压频率

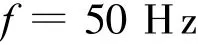
开关频率为

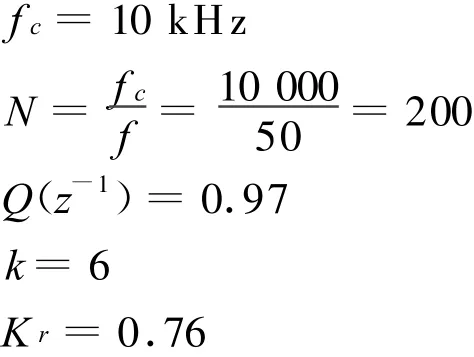
滤波电感

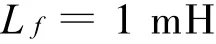
滤波电容

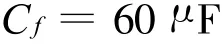
PID调节器的参数

重复控制器中的

PID控制输出电压波形和复合控制电压输出波形如图9和图10所示。

图9 PID控制输出电压波形

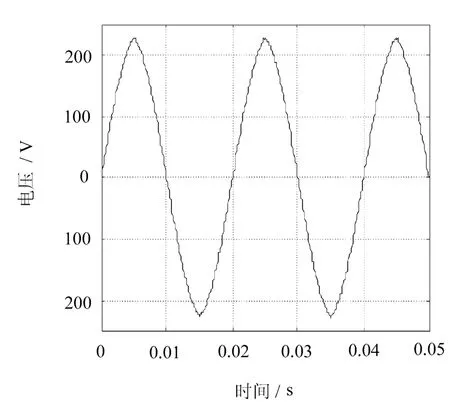
图10 复合控制电压输出波形

从仿真结果可以看出，PID控制输出电压波形畸变率比较大，纹波电流大，而复合控制输出波形则比较平滑，稳态误差小，输出更加接近于给定的220 V正弦波。

4 结 语

阐述了单相光伏逆变电源的结构组成，通过分析，逆变器采用双级结构，DC/DC部分采用Boost升压电路，并采用单周控制使输出电压稳定在400 V;DC/AC部分采用将有较好稳态性能的重复控制和较好动态性能的PID控制相结合组成的复合控制，并进行了仿真，从仿真图形可以看出，复合控制输出波形畸变小，具有较好的控制效果。

[1] 王子洋.单相逆变电源的智能控制研究[D]:[硕士学位论文].秦皇岛:燕山大学，2005.

[2] 郭卫农，陈坚.电压型逆变器输出波形控制技术[C].台达电力电子新技术研讨会论文集，2001: 129-133.

[3] 杨金辉，戴瑜兴，易龙强，等.基于重复控制原理的正弦逆变控制[J].电力电子技术，2010，44(5):65-66，72.

[4] 唐欣，马迎召，李红涛.基于重复控制的有源滤波器双闭环控制[J].电机与控制学报，2009，13(1):67-71.

[5] 胡文华，马伟明，刘春喜.一种新型交流PI调节器及其在逆变电源中的应用[J].电气传统，2010，40(1): 38-42.

[6] 李航金，新民.改进型重复控制的逆变电源[J].电气时代，2006(6):128-130.

[7] 于小辉，梁志珊.基于单周控制的三相光伏并网发电系统[J].电气自动化，2008，30(5):7-11.

[8] 卢秀和，王琪，陈军，等.双供电路灯调光节能技术研究[J].长春工业大学学报:自然科学版，2007，28 (1):75-78.