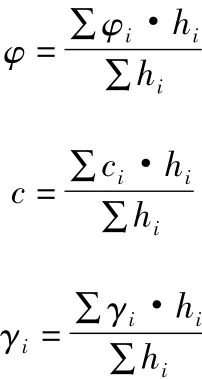浅谈圆弧滑动面的条分法

金碧蓉

(贵州省德江公路管理段)

1 原理

条分法是圆弧滑动面稳定性计算方法中具有代表性的方法。该方法的基本原理是静力平衡。同样假定土质均匀，不计滑动面以外的土体位移所产生的作用力，计算时取单位长度，将滑动体划分为若干土条，分别计算各土条对于滑动圆心的滑动力矩Moi和抗滑力矩Myi，取两力矩之比值为稳定系数K，据以判别边坡是否稳定。此时K值为

分条可以使计算结果较为精确。稳定系数最小值Kmin，是通过多道圆弧曲面试算而得，计算工作量较大，所以分条也不宜过多。条分法要求作图准确，尽量减少量取尺寸的误差。

2 图式

图1为圆弧滑动面的计算图式，首先确定圆心O和半径OA。一般情况下，圆心的位置 是在圆心辅助线EF的延长线上移动，E点和F点的位置可用以下的4.5H法确定。

图1中边坡计算高度H=h1+h0，由A点作垂直线，取深度为H确定G点，由G点作水平线，取距离为4.5H确定E点，即4.5H法。F点位置由角度β1和β2的边线相交而定，其中β1以AB′平均边坡线为准，β2以B′点的水平线为准，如果不计荷载，则h0=O，B′由B代替。β1和β2取决于路基的边坡率。

大量计算证明，如果路基边坡为单斜线，坡顶为水平，当φ=0时，最危险滑动面的圆心，就在F点上。当φ＞0，圆心在辅助线上向左上方向移动，φ值愈大，OF间距愈大，通常取4～5点为圆心，分别求K值，并绘制K值曲线，据以解得Kmin值及相应的圆心O0。

圆心辅助线亦可用36°线法绘制。36°线法比较简便，但计算结果误差较大，可在试算中使用。

3 计算式

将滑动体分成若干土条，分条计算作用力和力矩，采用下式计算稳定系数K值。

图1 4.5H线法确定圆心位置图式

式(4－8)中半径R已消去，分子中∑Ti为代数和。各土条的法向分力Ni和切向分力Ti可绘制曲线。

路基填土的计算参数，内摩擦角φ、黏聚力c及重度γ，一般均取固定数值。当路基分层填筑，参数相差较大时，可取加权平均值。设土层厚度为hi，则: