弹性波勘探方法组合在公路检测中的应用

柳光伟，刘洪津

(1.黑龙江省煤田地质测试研究中心;2.辽宁省核工业地质局241大队)

1 公路各结构厚度检测

(1)共振法超声波法组合测定路面厚度

图1是水平层状结构弹性体系公路结构层模型。

图1 水平层状结构弹性体系公路结构层模型

图1中，路基包括了基层和路基，p1、p2分别为路面、路基的密度;vp1、vs、vp2、vs2分别为路面、路基的纵波和横波速度;E1、E2分别是路面、路基的刚度H(或h)为路面厚度。

当表面施加一频率为f的简谐振力时，则在x≈±r0的范围内，沿Z方向传播的波特性可以看做一维状态，设单位面积的作用力为Fejωt，沿Z方向波的传播方程为:

式中:Uz为介质质点沿Z方向的位移，公式表明，力Fejωt在路面内产生的纵波(压缩或拉伸)是以速度vp传播的。该波动方程的解可写成如下形式

式中:U(z)为路面震动函数。将上式代入(1)式得U(z)的微分方程

设式(3)的解为

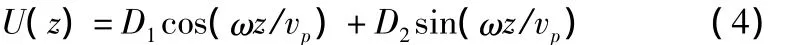
则(2)式可写成

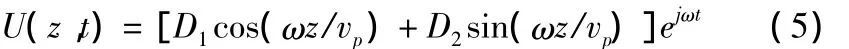
式中的D1、D2为常数，可由边界条件确定:即在表面界面上(Z=0)，应力等于作用力，在路面底界面两侧应力相等

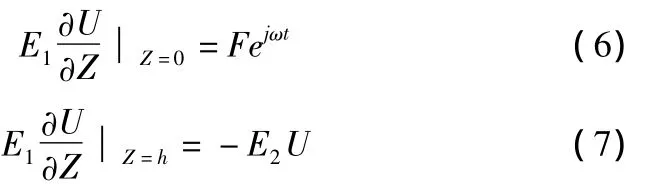
把(4)式分别代入(6)和(7)式，最后求得

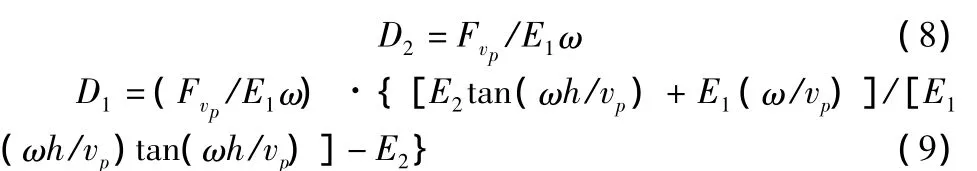
由此，可求得路面上(Z=0)的位移U(0，t)的表达式

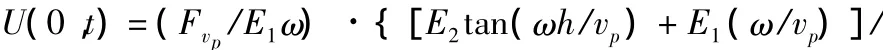
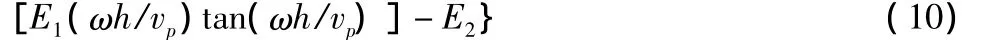
可见，U(0，t)的振幅与频率(ω=2πf)，厚度H和波速vp有关，对给定的检测对象，H和vp是定值，所以振幅只与频率有关。下面两种情况讨论U(0，t)的振幅特性。

①当E2=∞，即面层的下伏层为坚硬层，则式(10)中U(0，t)的振幅变为

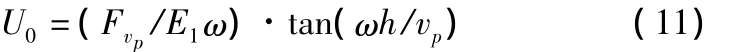
分析(11)式样可知

当ωh/vp=nπ时，U0=0，(n=1，2，3，…)

当ωh/vp=1/2(2n－1)π时，U0=∞，(n=1，2，3，…)

根据共振现象的定义可知，当ωh/vp=1/2(2n－1)π时即发生共振，这时的频率定义为共振频率f0。公式表明，当下伏层刚度为无限大时，其最低共振频率(n=1)为

检测出共振频率f0和vp后，即可求出路面厚度

以上讨论的情况，相当于公路路面是柔性介质，基层是刚性介质，一般很少遇到，没有代表性。

②E2=0，公路面层下伏层为较软基层，即E2＜E1，大多数公路结构层属于这种情况，这时(10)式振幅项变为

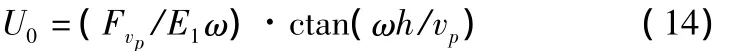
分析上式可知

当ωh/vp=nπ时，U0=∞，(n=1，2，3…)

当ωh/vp=1/2(2n－1)π时，U0=0，(n=1，2，3…)

这时的最低共振频率为

厚度计算公式为

用共振法确定f0，超声波法求出vp，即可计算出路面厚度，把每一测点的厚度构成断面，就可以了解其厚度的变化。

图2是利用(14)式，结构面层和路基参数分别为vp1= 4000m/s，E1=3500MPa，vp2=600m/s，E2=350MPa，H= 0.25计算的频幅曲线。由式(15)计算，给定模型的最低共振频率f0=8000Hz，第二、第三共振频率分别为16000Hz和24000Hz，从图中可见，由(14)和(15)式得到的共振频率是一致的。图中实线为理论曲线，虚线为实测曲线。实测时振幅不可能无限大，这是因为周围介质对振动有阻尼，能量在扩散和衰减。

图3是路面厚度不同，其他参数与上图相同条件下计算的幅频曲线2。由图可见，不同的路面厚度共振频率各不相同，分别是8000Hz、8300Hz、8700Hz、9100Hz、9500Hz、10000Hz。一般水泥混凝土路面厚度为0.22m，当厚度变化为0.01m时，共振频率变化为400Hz，亦即厚度的微小变化可引起共振频率的较大变化，一般仪器频率分辨率可达10Hz左右，所以用共振法检测厚度误差，理论上可控制在±1mm左右。

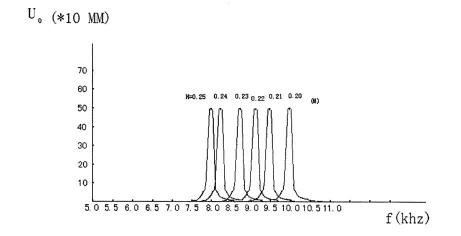
图2 频幅曲线1

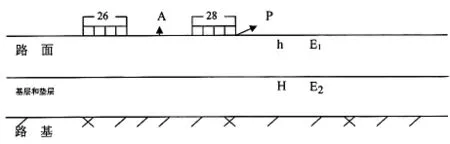
图3 频幅曲线2

(2)瑞雷波法测定公路的结构层厚度

刚性路面一般只要求测定路面厚度，而柔性路面的主要质量控制指标是弯沉降值，它除与路面厚度有关外，还与其他各结构层厚度密切相关，为此，必须测定出各结构层的厚度。通常采用瑞雷波法。

应用瑞雷波法测定结构层的厚度是基于在层状介质中瑞雷波频散曲线的变化频率，它除与各层的物理参数有关外，还与各层厚度密切相关，尤其是频散曲线的拐点，即(vR瑞雷波速度，波长)极值点，只与各层厚度相关。

各层的界面深度

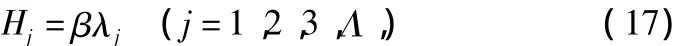
式中:Hj为第j层底界面深度，m;β为系数，可取0.35～0.5; λj为极值点处对应的波长，m。

确定了各层的底界面深度，就不难计算出各层的厚度。

2 瑞雷波法或超声波法测定压实度

柔性路面、基层、路基的压实程度，对其强度和稳定性影响极大。已知压实度定义为利用弹性波速度测定压实度K是基于速度与密度间存在的相关关系，由弹性理论已知:

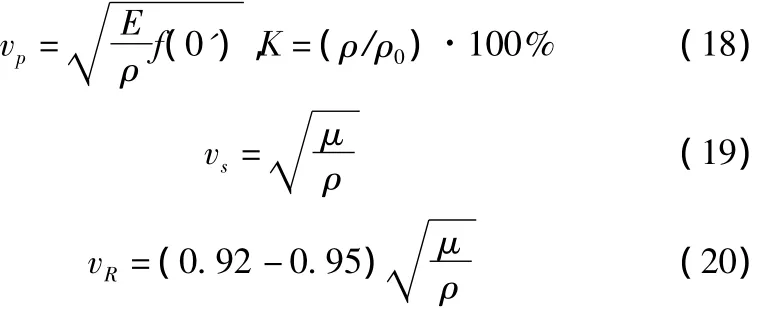
式中:vP、vS、vR分别是纵波速度、横波速度和瑞雷波速度;E、μ是压缩量和剪切模量。ρ泊松比。

公式似乎表明，当密度ρ增大时，波速会降低，其实不然，因为对给定的介质，密度是介质孔隙度的函数。压实程度增大，孔隙度减小(变密实)将使ρ增大，同时E、μ和vP也增大，它们比起密度ρ增大要快得多，结果导致vP、vS、vR也相应增大。根据这一规律就可建立密度与波速间相关关系，研究表明，呈下列幂函数形式

式中:A1、B1、A2、B2为常数。在双对数坐标中，该表达式是一直线

或

则压实度K用波速度表示为

式中:vP、vR是与实际压实密度ρ相应的纵波和瑞雷波速; vP0、vR0是与最大密度ρ0相应的纵波和瑞雷波速;B1、B2由统计分析求取。

3 瑞雷波法和超声波法组合测定路面强度

物质的力学性质在材料力学理论中，通常由其压缩模量E，剪切模量μ和体变模量K来表征。这三个模量的定义如下:

压缩模量定义为单位面积上垂直外力比产生的相对变化量

式中:P为是外力，N;S为物体的承压面积，mm2;△L为外力作用下产生的变形量，mm;L为物体的原来长度，mm。

剪切模量定义为单位面积的剪切外力比角度的变化量

式中:P为剪切外力，N;S为物体承受P的面积，mm2;φ为角度变化量(弧度)。

体变模量定义为单位面积上外力比物体体积的相对变化量

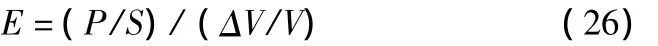
式中:P为外力，N;S为承压面积，mm2;△V为在P的作用下体积变化量，mm2;V为原体积。

由上列定义表达式可见，水泥混凝土的抗压强度R压在抗折强度R折与其E、μ、K均反映了力学性质，弹性模量值越高水泥混凝土的强度也越大，之间存在一定的相关关系

式中:A、B、C、D为相关系数。

在弹性波理论中，若纵波速度vP、横波速度vS和密度ρ，物体的力学性质也完全可表征出来，与E、μ、K表征完全是等价的，之间有如下关系

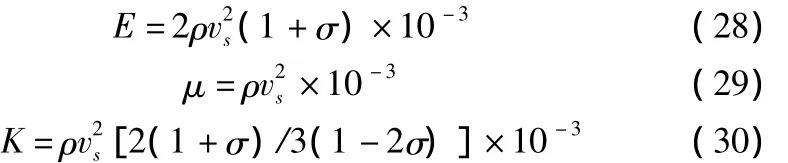
可见，只要测定波速(vp、vS)，已知密度ρ，即可求得混凝土的弹性模量，用统计分析法求取相关系数，再由式R折= R压可求出抗压强度(AR压+B)求得抗压强度R折。这就是利用波速评估水泥混凝土路面强度的原理。

水泥混凝土路面为一块薄板状体，为精确的测定出波速vP和vS，就要使工作频率相应波长λ小于板的厚度。因此，vP测量采用超声波法，vS测量采用瑞雷波法，用大于8000Hz瑞雷波先测得vR值，再由vS≈vR/0.92，近似求得vS。通常密度ρ为已知，公路交通部门可用3411－B型核子湿度密度仪测定。