裂纹萌生寿命预腐蚀影响规律

金 平，王 刚，谭晓明

（海军航空工程学院青岛分院，山东 青岛 266041）

0 引言

海军飞机在沿海一带服役，使用环境恶劣，环境对飞机结构的腐蚀损伤非常严重，研究表明，地面环境的腐蚀作用是影响军用飞机结构的主要因素。[1-2]由于飞机结构形式的复杂性和结构、环境等的分散性，难以准确对腐蚀损伤进行测定。从工程实用的角度出发，通常以腐蚀时间来衡量腐蚀损伤，研究疲劳性能随时间的变化规律[3]。在腐蚀环境下的飞机结构耐久性分析的相对小裂纹范围内，不同裂纹尺寸对应的预腐蚀裂纹萌生寿命不同，如果不同裂纹尺寸对应的C-T曲线参数不一样，则增加了分析的复杂性，从而有必要对预腐蚀条件下飞机结构裂纹萌生预腐蚀影响系数和裂纹尺寸的关系进行分析，研究预腐蚀对裂纹萌生寿命分散性的影响和指定裂纹尺寸下裂纹萌生寿命的变化规律。本文对比分析了4种C-T曲线函数形式对不同裂纹尺寸对应的裂纹萌生寿命预腐蚀影响系数C的影响，研究了各函数形式在不同裂纹尺寸下拟合效果的差异性，为腐蚀环境下飞机结构耐久性分析奠定了基础。

1 裂纹萌生寿命分布规律和分散性

理论研究和试验结果表明，一般环境对同一应力水平进行疲劳试验时，在中、短寿命区，对数疲劳寿命遵循正态分布[4]；预腐蚀时间T后，一般环境下结构疲劳寿命服从对数正态分布[2，5]。采用文献[6]附表2中歼X型飞机机翼后梁模拟试件加速预腐蚀不同时间后，一般环境下谱载荷下裂纹扩展试验数据，取σ=312.9 MPa 对应的裂纹扩展数据，由Matlab 三次样条插值计算裂纹尺寸a为0.4、0.6、0.8、1.0 mm时对应的裂纹萌生寿命，对数中值裂纹萌生寿命与预腐蚀时间对应关系见图1，(a,N)数据及相关统计数据见表1。从表1和图1中可以看出，不同裂纹尺寸下的对数裂纹萌生寿命下降梯度基本一致。给定显著水平a=0.05，F 检验表明，预腐蚀后指定裂纹尺寸裂纹萌生寿命与未腐蚀裂纹萌生寿命方差无显著差异，即在工程常用的时间范围内，裂纹萌生寿命分散性与预腐蚀时间无关，且上述不同的指定裂纹尺寸对应的裂纹萌生寿命具有方差齐性：有综合标准差sw=0.222 8。

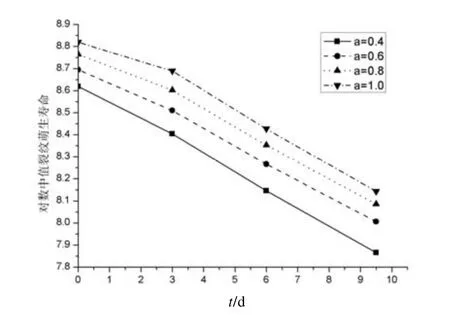
图1 对数中值裂纹萌生寿命与预腐蚀时间对应关系

表1 给定裂纹尺寸的裂纹萌生寿命及数据处理结果

2 裂纹萌生寿命预腐蚀衰减规律

2.1 (C,T)数据的线性回归分析

工程上往往不直接建立疲劳寿命随腐蚀时间的变化，而是研究预腐蚀对疲劳寿命的影响，建立疲劳寿命相对变化随预腐蚀时间的变化规律，由此引入预腐蚀影响系数C(T)[1]。若预腐蚀时间T后指定裂纹尺寸下的裂纹萌生寿命服从对数正态分布，根据预腐蚀疲劳寿命影响系数C(T)的统计表达式[7]，可求得指定裂纹尺寸下裂纹萌生寿命预腐蚀影响系数C(T)如表1所示。

将4种典型的C-T曲线函数形式[5-6]通过取对数进行线性化处理，利用最小二乘法对表1中的(C,T)数据进行拟合，得到的相关参数见表2。其中，r为相关系数，σe2为剩余方差，lxx表达式见文献[5-6]。

通过相关系数检验，各函数形式的拟合结果都具有良好的线性趋势，且相关系数差别不大，由给定裂纹尺寸的剩余方差可知幂函数形式和双参数指数函数形式③在给定裂纹尺寸0.8mm、1.0mm的拟合的误差相对比较大。

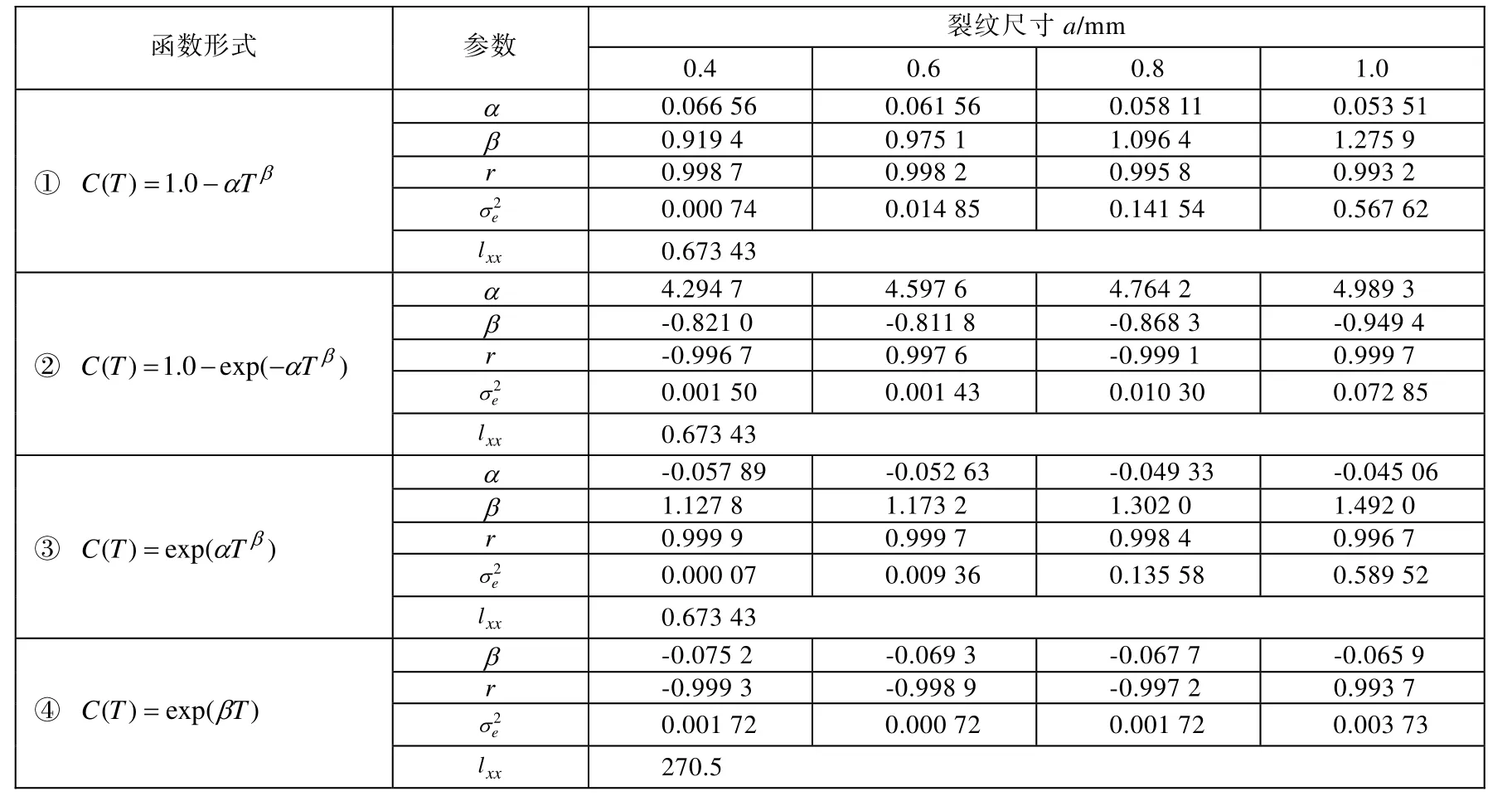
表2 (C,T)数据拟合的相关参数

2.2 C-T曲线参数的统计对比分析

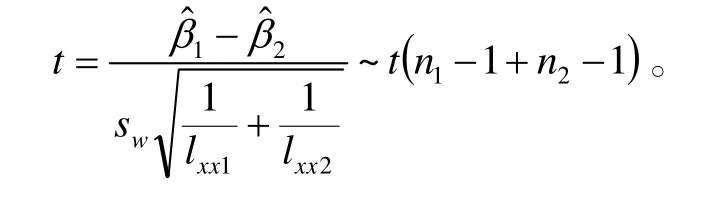
如果C-T曲线参数经检验无差异，则说明C-T曲线具有通用性[5]。给定显著水平α 进行t 检验，分别选取4种函数形式拟合的C-T曲线斜率相差最大的两组进行参数检验。给定α=0.5，经t 检验4种函数形式的C-T曲线斜率参数均通过了t 检验，从而说明4种函数形式拟合的C-T曲线参数均无差异，C-T曲线参数与裂纹尺寸基本无关，不同裂纹尺寸对应的C-T曲线具有通用性。

2.3 C-T曲线拟合效果对比分析

对比分析4种函数形式拟合的C-T曲线如图2～5所示，可知幂函数形式和双参数指数函数形式③在裂纹尺寸0.8 mm、1.0 mm 对应的拟合曲线在预腐蚀约3.5 d（约15 a）之后出现了相对比较大的误差，这说明在以这两种函数形式拟合的不同裂纹尺寸对应的裂纹萌生寿命预腐蚀影响系数C(T)通用性相对比较差，而双参数指数函数形式②和单参数指数函数形式拟合效果较好，相比较而言，单参数指数函数形式拟合效果最好，具有较好的通用性。综合不同裂纹尺寸下的单参数指数函数形式的参数可得公共参数β=−0.069 525。因此，在腐蚀环境下的飞机结构耐久性分析中，不同的裂纹尺寸对应的裂纹萌生预腐蚀影响系数C(T)宜采用单参数指数函数形式拟合。

图2 幂函数式C-T曲线图

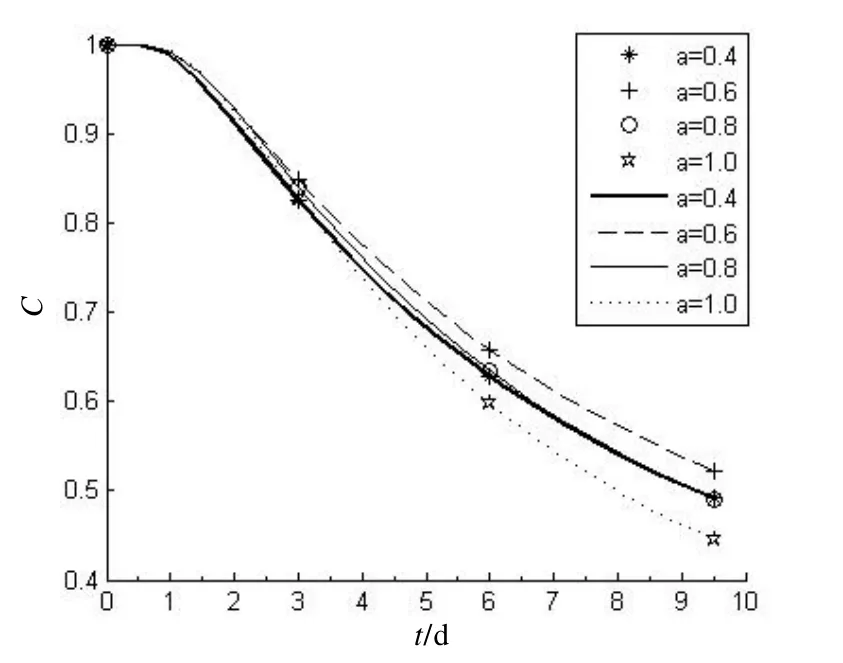
图3 双参数指数函数②C-T曲线图

图4 双参数指数函数③C-T曲线图

图5 单参数指数函数式C-T曲线图

3 结论

1)在工程常用的时间范围，裂纹萌生寿命随预腐蚀时间的增加而降低，且不同裂纹尺寸下的对数裂纹萌生寿命下降梯度基本一致。若假定裂纹萌生寿命服从对数正态分布，则对数裂纹萌生寿命分散性不随预腐蚀时间变化。

2)裂纹萌生寿命预腐蚀影响系数C(T)随时间变化规律可用指数或幂函数拟合，对比分析以上4种函数形式，不同裂纹尺寸对应的C-T曲线参数均无显著差异。相对而言，单参数指数函数拟合效果最好，对不同裂纹尺寸对应的预腐蚀影响系数C(T)具有较好的通用性。

[1]刘文珽,李玉海,贾国荣.腐蚀条件下飞机结构使用寿命评定与监控方法研究[J].北京航空航天大学学报,1996,22(3):259-263.

[2]杨晓华.腐蚀累积损伤理论研究与飞机结构日历寿命分析[D].南京:南京航空航天大学,2002:29-31.

[3]贺小帆,刘文珽,王忠波,等.预腐蚀对30CrMnSiNi2A连接件疲劳寿命影响的试验研究[J].机械强度,2009,31(4):664-669.

[4]高镇同,熊峻江.疲劳可靠性[M].北京:北京航空航天大学出版社,2000:74.

[5]贺小帆,刘文珽,向锦武.C-T曲线通用性分析和试验研究[J].航空学报,2005,26(2):184-189.

[6]贺小帆.腐蚀条件下飞机结构寿命可靠性关键技术研究[D].北京:北京航空航天大学,2003.

[7]赵学锋,王富永,赵海军.预腐蚀疲劳寿命影响系数及S-N曲线研究[J].机械强度,2008,30(6):977-981.