一种弹目遭遇点预测方法

张友安，马国欣，2，万 宇

（1.海军航空工程学院控制工程系，山东 烟台 264001；2.93132部队，黑龙江 齐齐哈尔 161016；3.海军装备部军械保障部，北京 100083）

舰空导弹为实现超视距拦截，导弹通常采用初制导+中制导+末制导的复合制导体制。中制导律设计的主要任务是将导弹导引到目标附近，以较好的弹目相对几何关系转入末制导，同时要求导弹在中制导段尽量节省能量和飞行时间。

预测遭遇点是导弹命中目标的预计位置，如果预测准确，那么它就是空间中的一个固定位置，实际中预测的遭遇点变化速度也很小。因此，基于预测遭遇点的中制导律设计将大大提高弹目速度比，减小拦截弹道需用过载，提高命中精度。

文献[1-2]假设导弹采用传统比例导引飞至预测遭遇点，通过解算导弹至遭遇点的剩余飞行时间以及目标至遭遇点的剩余飞行时间，并结合弹目相对几何关系，最终给出了导弹对遭遇点的制导指令所需信息。文献[3]采用最优控制的方法将导弹导引到预测交班点，导弹到达交班点时末速度指向实际目标。文献[4-5]通过迭代求解的方法确定拦截弹道导弹的预测命中点，而文献[6]则通过解算战术弹道导弹被动段的运动学方程来估计预测命中点。文献[7-9]根据视线法及比例导引法来解算导弹的运动学弹道，从而获得瞬时遭遇点的坐标。文献[10]采用龙格库塔法，给出了一种能够使飞行器与运动目标交会的命中点预测方法，并据此完成了飞行器需用速度的确定。文献[11]根据观测的机动目标在若干时刻之前的信息，应用广义卡尔曼滤波算法实现对当前时刻机动目标的多步估计，并提出了将拦截导弹直接向瞬时遭遇点导引的末制导导引方法。

为避免复杂的方程求解或迭代算法，本文依据弹目相对几何关系及导弹中制导导引特性，给出一种工程实用的遭遇点实时预测方法。

1 遭遇点的解算

在初始发射坐标系中，导弹与目标的相对运动关系如图1所示。

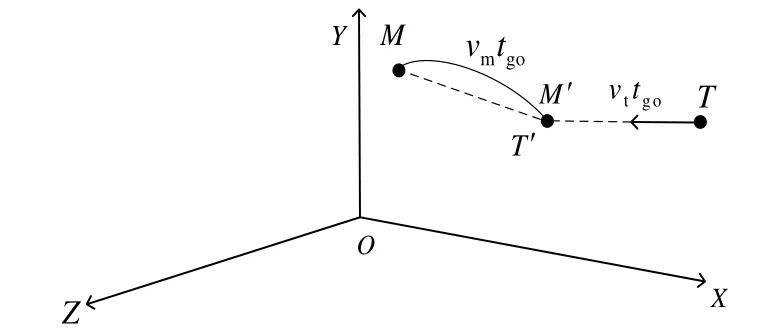
图1 遭遇点实时预测示意图

图1中，M表示当前时刻的导弹位置，T表示当前时刻的目标位置，M′表示飞行 tgo时间后的导弹位置，T′表示飞行 tgo时间后的目标位置，M′与T′重合表示导弹与目标遭遇。

假设目标以当前速度匀速直线运动至遭遇点，导弹以当前速度按照传统的比例导引规律匀速运动至遭遇点。实际中，目标在视距外机动的可能性不大，并且由于遭遇点的预测在线动态进行，随着导弹距遭遇点越来越近，期望弹道逐渐趋于平直，所以该假设具有合理性。

导弹当前位置为(xm,ym,zm)，当前速度为vm，目标的当前位置为(xt,yt,zt)，当前速度为vt，目标当前速度在初始发射坐标系3个坐标轴上的分量为(vtx,vty,vtz)，经 tgo后，导弹到达 M ′=(xm′,ym′,zm′)处，目标T到达 T ′=(xt′,yt′,zt′)处，参见图1。

根据空间几何关系有

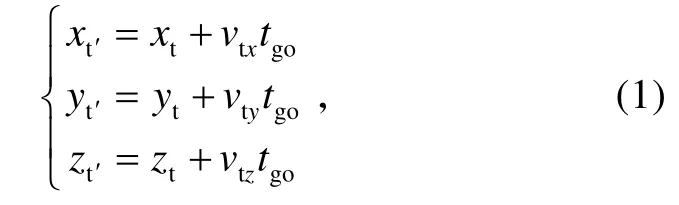
那么，M 距T′的直线距离为

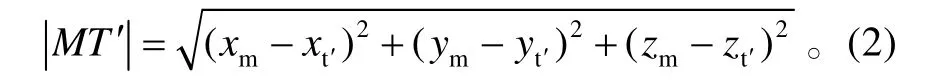
由假设条件可知，M 至T′的总航路大小为vmtgo，期望的导弹弹道趋于平直，所以认为

综合式(1)～(3)，整理可得

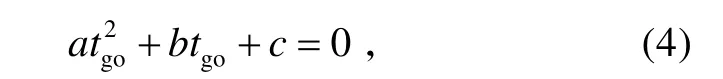
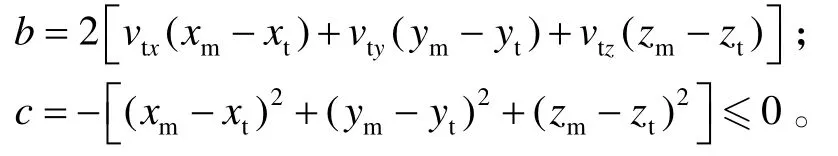
下面分3种情况讨论方程(4)的解：

①当a=0时，tgo=−c/b；

综上可得

至此，预测遭遇点的位置信息由式(1)和式(5)给出。对于当前时刻而言，导弹直接对该预测遭遇点进行攻击，当前时刻遭遇点的速度取为零。理想情况下，预测的遭遇点固定不变，导弹采用比例导引攻击该固定遭遇点时，其后期弹道趋于平直，说明了算法的可行性。

2 过载指令的生成

遭遇点位置信息(xt′,yt′,zt′)已知后，将遭遇点视为固定目标，弹目空间相对运动关系[12]为

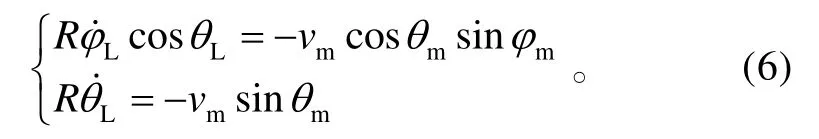
视线角速率信息获得后，可以解算出导弹的纵向比例导引过载指令为

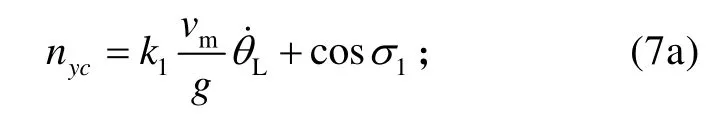
导弹的侧向比例导引过载指令为

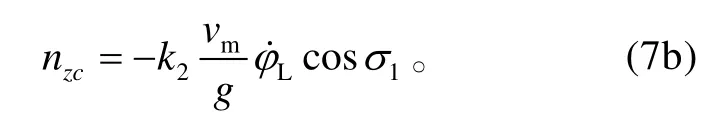
3 仿真分析

选择仿真初始时刻 t0=0 s，导弹初始位置(xm0,ym0,zm0)=(1 300 m,1 100 m,−2 000 m)，导弹初始弹道倾角30°，初始弹道偏角10°，导弹恒速运动，速度大小为1000 m/s；真实目标初始位置(xt0,yt0,zt0)=(70 000 m,10 m,−10 m)，以300 m/s的速度平飞，弹道偏角180°；将导弹视为一阶延迟环节取延迟时间 τ=0.1 s，采用拦截预测遭遇点的比例导引制导律，导弹过载限幅为20 g，仿真步长取为0.001 s，仿真结果如图2所示。

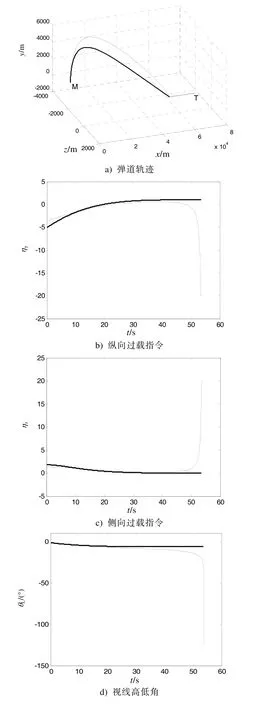
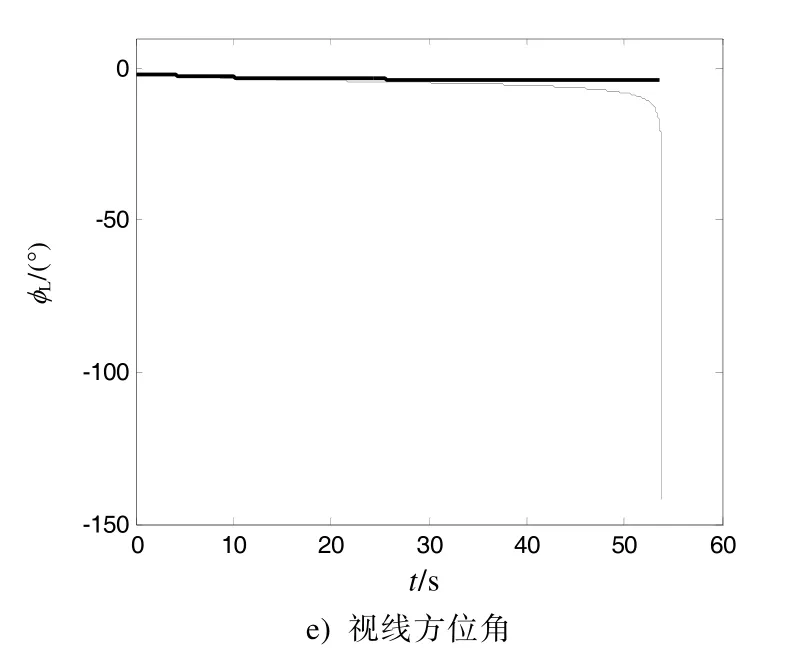
图2 拦截预测遭遇点与拦截真实目标的比例导引仿真结果

图2中，粗实线代表拦截预测遭遇点的比例导引仿真结果，其脱靶量为48.45 m，细实线为拦截真实目标的比例导引仿真结果，其脱靶量为2.51 m。直观上，拦截预测遭遇点比例导引的弹道更为平缓，尤其在导引后期能够避免过大的弯曲，正如图2a)所示。相比之下，随着导弹与目标越来越近，导弹采用拦截真实目标比例导引时，其过载越来越大，参见图2b)、图2c)。

对于匀速直线运动的目标，随着导弹弹道逐渐趋于平直，其遭遇点解算越来越精确，直到预测的遭遇点固定不变。于是拦截预测遭遇点的比例导引便具备攻击固定目标时比例导引的特性，其视线角逐渐趋于定值，参见图2d)、图2e)。这意味着实际目标的视线角速率趋于0，当导弹转入末制导时，其需用过载很小。

为进一步验证导弹速度变化且目标机动情况下遭遇点解算方法的有效性，导弹的初始速度取为750 m/s，采用形式的速度变化规律来模拟导弹速度的变化；目标初始弹道偏角取为180°，以300 m/s的速度在水平面作蛇行机动，目标法向加速度为atn=100cos0.5t (m/s2)，其余仿真条件不变，仿真结果如图3所示，其脱靶量为2.79 m。结果表明，对于导弹速度变化且目标机动的情况，该遭遇点解算方法能够适用，拦截预测遭遇点的比例导引具有较好的效果。

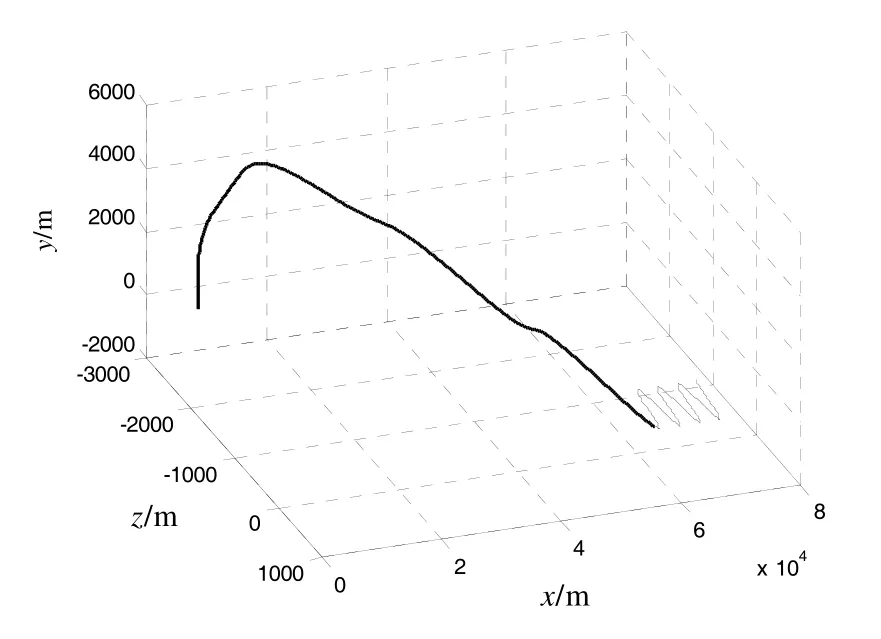
图3 导弹速度变化且目标机动时的仿真结果

4 结论

对于超视距拦截问题，本文依据弹目几何关系及导引特性，给出了一种遭遇点实时预测方法，该方法直接给出了遭遇点的解析解形式，避免了复杂的方程求解或迭代求解，具有工程实用性。无论对于匀速直线运动的目标或是机动目标，基于该预测遭遇点的比例导引制导方法都能够有效减小需用过载，优化过载分布，从而提高命中率。

[1]余名哲,张友安,钱进.基于遭遇点预测的比例导引与多平台接力制导交接律设计[J].海军航空工程学院学报,2010,25(3):255-258.

[2]余名哲.大指示误差情况下协同制导方法研究[D].烟台:海军航空工程学院,2010:47-51.

[3]董朝阳,周雨.一种交班时刻性能最优的中制导律设计与仿真[J].系统仿真学报,2009,21(24):7873-7882.

[4]张化伟,董茜,王文灿,等.基于预测命中点的反弹道导弹拦截方法研究[J].弹箭与制导学报,2007,27(2):196-199.

[5]韩雁飞,王希望.导弹拦截时TBM 落点及命中点预测模型[J].海军大连舰艇学院学报,2002,25(6):41-43.

[6]李荣宁,刘敏.中远程战术导弹预测命中点的计算[J].现代防御技术,2001,29(3):23-26.

[7]王君,周林,雷虎民.低空导弹与空中目标遭遇点预测模型和算法[J].系统仿真学报,2009,21(1):80-83.

[8]侯明善.指向预测命中点的最短时间制导[J].西北工业大学学报,2006,24(6):690-694.

[9]一辉.当今俄罗斯主力舰艇防空导弹系统与集成方式解析[J].现代兵器,2008(1):6-11.

[10]于桂杰,罗俊,赵世范,等.基于龙格库塔法的预测闭路制导方法研究[J].航天控制,2008,26(5):41-44.

[11]赵文成,金学英,那岚.末制导段比例导引法的改进[J].火力指挥与控制,2009,31(4):97-99.

[12]张友安,胡云安.导弹控制和制导的非线性设计方法[M].北京：国防工业出版社,2003:156-157.