反潜巡逻机反潜战术机动建模与仿真
刘新科,罗木生,向述乐
(1.西北工业大学航海学院,西安 710072;2.海军大连舰艇学院,辽宁 大连 116018;3.海军航空工程学院研究生管理大队,山东 烟台 264001;4.91960部队,广东 汕头 515074)
反潜巡逻机以其较强的反潜能力和对大范围海域的监控能力,已成为航空反潜的主要兵力。结合近年来发展起来的仿真技术,对巡逻机反潜过程进行仿真,既能用于作战模拟系统中的战场态势显示,也可应用于巡逻机反潜过程的模拟训练。然而,巡逻机反潜过程的仿真系统研究中,建立其战术机动模型是关键一环。
关于战斗机机动模型的研究较多[1-3]。本文在分析巡逻机反潜作战过程的基础上,将战术机动过程转化为两点间的飞行机动问题并建立了巡逻机反潜战术机动模型,较好地解决了飞行参数解算与机动航线选择问题。
1 反潜巡逻机反潜战术机动过程描述
巡逻机在反潜过程中,无论是使用搜潜器材搜索,还是使用武器攻击目标,都需要在选定合适的搜潜或攻潜样式后,机动到相应阵位才开始搜索或攻击,尤以使用声纳浮标搜潜所需的机动“占位”最多。不失一般性,现以使用声纳浮标为例进行说明。
声纳浮标是巡逻机搜潜的主要手段之一,其搜索阵形有线形阵、圆形阵、方形阵等[4]。使用声纳浮标搜潜的一般过程为[5]:根据布设阵形确定所有声纳浮标投布点后,巡逻机先降高到浮标投放高度;接着机动到第一个投布点投放声纳浮标,完成后机动到第二个投布点,直至声纳浮标阵布设完毕;然后爬高到侦听高度监听声纳浮标发射的无线电信号;发现可疑目标后,巡逻机机动到发现目标的声纳浮标上空布设定位浮标阵;完成定位后,巡逻机机动到攻击阵位攻击目标。
根据上述作战过程,巡逻机的战术机动可分解为若干个从A点到B点的机动,那么,巡逻机的战术机动模型就转化为任意两点间机动的数学模型。为满足通用性,所建立的机动模型需适应任意情况,即:A、B两点间的距离任意,且进入A点的方向和到达B点的方向都是任意的。同时,为符合实际机动要求,两点间的机动航线距离应最短且转弯数量最少。
2 反潜巡逻机反潜战术机动建模
巡逻机不能悬停,也不必迎风飞行,而是可能从任意方位角进入某一航路点,也可能以任意方位角飞出另一航路点,故其机动模型较直升机更为复杂[6]。巡逻机高度的变化量可根据爬升率解算得出,因而,本文主要分析反潜巡逻机等高机动时的机动航线和飞行参数。
假设反潜巡逻机从A点机动到B点,则以A点为原点,Y轴正方向为进入A点的方位角,垂直Y轴向右为X轴正方向,建立水平面上的平面坐标系。通过分析可知,对于任意位置上的B点,在最小转弯数的前提下,从A到B可行的机动航线最多有4条,如图1所示。图中,AΨ为进入A点的方位角,为到达B点的方位角。

图1 可行的4种机动航线图
图1a)是先顺时针转弯,图1b)是先逆时针转弯,最终都是以方位角 BΨ通过B点。为便于后文建模分析,根据转弯方向,对4条可行的机动航向进行定义,如表1所示。

表1 可行的机动航线
不论采取哪条航线机动,都需要建立模型,解算两个转弯角度、转弯间的直飞距离等参数。不失一般性,现以顺逆转弯机动航线为例,对各飞行参数进行分析和定义,其他机动航线类似。设两个转弯角度分别为ϕ1、ϕ2,直飞距离L,如图2所示。
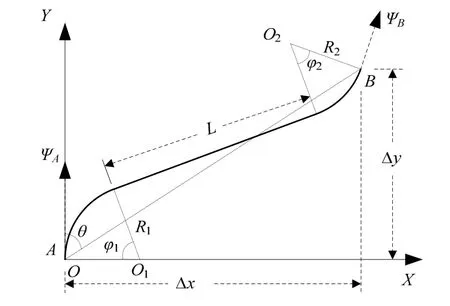
图2 反潜巡逻机水平方向上的机动航线图
模型中假定转弯段的转弯半径不变,且不得小于最小转弯半径,从而保证反潜巡逻机转弯时不会超过飞机的最大过载。
由A、B点的经纬度,以及进入A点的方位角AΨ、到达B点的方位角 BΨ,可计算出A、B在水平面上的距离DAB和A指向B的方位角 AΨ,则有
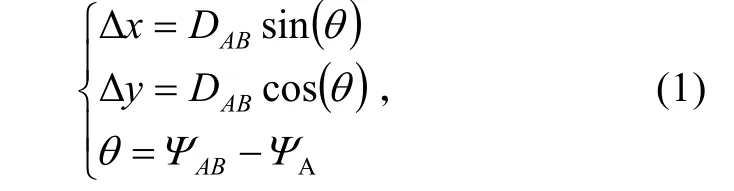
式中:Δx、Δy分别为距离DAB在X轴方向、Y轴方向的分量;θ为从 AΨ到ΨAB的角度差。
根据上述分析和定义,下面分别求解4种可行机动航线的飞行参数。
2.1 顺顺转弯机动航线
顺顺转弯机动航线是从A点开始顺时针转弯,直飞L后,再顺时针转弯以方位角 BΨ通过B点。由于转弯角度计算时涉及反三角函数的求解,因而需要考虑角度ϕ1所处的象限,如图3所示。
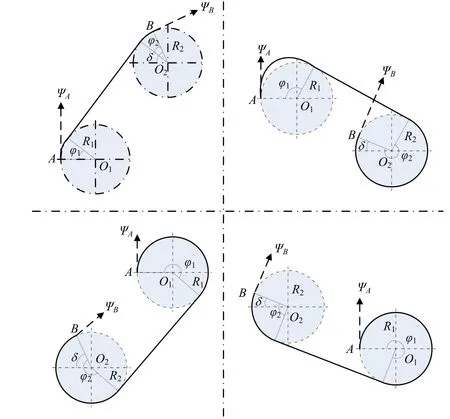
图34 种可能的顺顺转弯示意图
根据位移关系,建立模型如下:

令 a=(R1−R2),c=Δy−R2sin(δ),d=Δx−R1+Rc2os(δ),解算得:

2.2 顺逆转弯机动航线
顺逆转弯航线是从A点开始顺时针转弯,直飞L后,再逆时针转弯以方位角 BΨ通过B点。根据角度ϕ1所处象限,也需考虑类似图3所示的4种可能的情况。根据位移关系,建立如下模型:


2.3 逆顺转弯机动航线
逆顺转弯航线是从A点开始逆时针转弯,直飞L后,再顺时针转弯以方位角 BΨ通过B点。根据角度ϕ1所处象限,也需分析4种可能的情况。根据位移关系,建立如下模型:

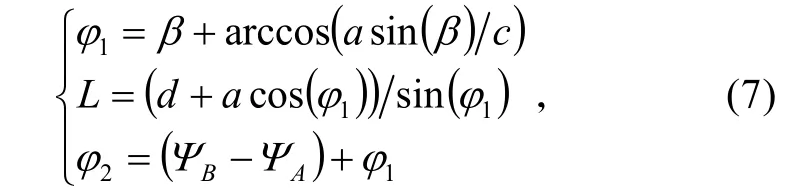
2.4 逆逆转弯机动航线
逆逆转弯航线是从A点开始逆时针转弯,直飞L后,再逆时针转弯以方位角 BΨ通过B点。同理,根据角度ϕ1所处象限,分析4种可能的情况。根据位移关系,建立如下模型:
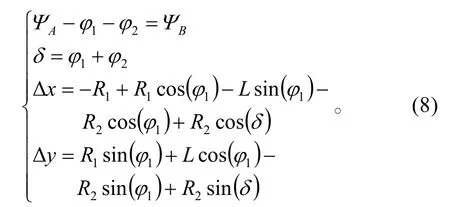

2.5 航线选择模型
上述各航线的模型和求解已经给出,但是当角度 ϕ1位于第三、第四象限,即 ϕ1∈[1 80,360]时,解算出的ϕ1值仍属于第一、第二象限。简单的解决方法是,先定义
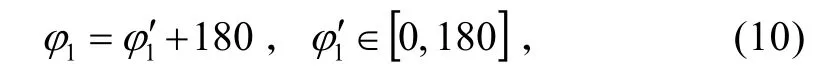
将其代入上述各航线的模型中,解算出 ϕ1′后代回上式,从而得出 ϕ1值,再求解其他参数。
解算出上述4种航线下的机动参数后,一般采用机动距离最短的航线k,即取满足k(k ∈{1,2,3,4})值,

3 仿真计算与分析
以反潜巡逻机布设声纳浮标阵为例进行仿真,验证上述战术机动模型。设反潜巡逻机投放声纳浮标时的飞行高度为1 000 m,飞行速度为350 km/h,最小转弯半径为3 km。为了计算声纳浮标投布点,设声纳浮标有效探测距离为4 km,布设间距不小于4 km,但不超过6 km。
依据反潜巡逻机投布声纳浮标的一般作战过程,结合战术机动模型,设计了仿真流程,见图4。依据仿真参数和仿真流程,对反潜巡逻机投布声纳浮标线形阵、圆形阵进行仿真。反潜巡逻机沿着图5a)、b)中的长划线布设线形、圆形声纳浮标阵,仿真效果如图5所示。图5中点虚线即为反潜巡逻机根据战术机动模型解算出的飞行参数,投布声纳浮标的飞行航迹。从图5中可以看出,反潜巡逻机的航迹平滑,能根据当前航向与相邻点间的距离、方位关系,解算出满足要求的航线,证明反潜巡逻机反潜战术机动航线模型的正确性。

图4 仿真流程图
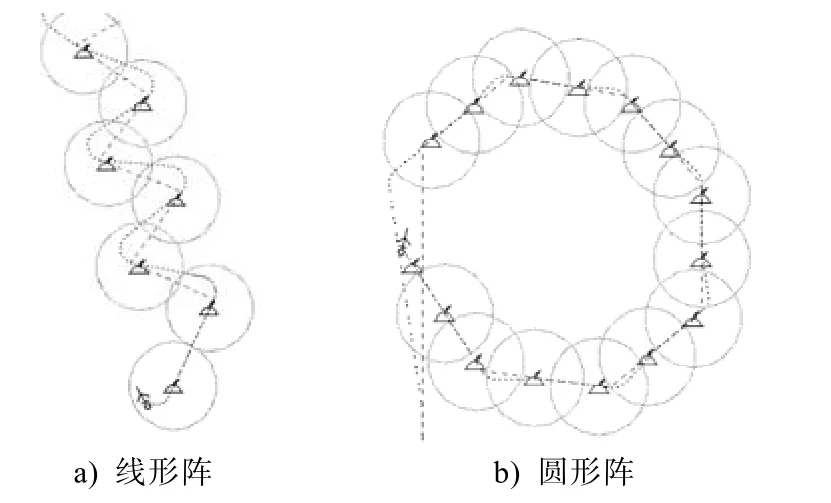
图5 二维机动仿真效果截图
4 结束语
本文在分析反潜巡逻机反潜作战过程的基础上,以使用声纳浮标搜潜为例,建立了反潜巡逻机反潜战术机动模型,实现了飞行航线参数的解算;通过仿真反潜巡逻机投布声纳浮标的战术机动,验证了模型的正确性。本文建立的战术机动模型,对反潜巡逻机的战术机动仿真程序的开发、反潜战术研究与战场态势显示等,具有一定的指导意义和参考价值。
[1]黄智勇,姜昱明.超机动飞机的数学建模与运动仿真[J].微电子学与计算机,2007,24(11)∶53-56.
[2]刘勋,高正红,商重阳.空战仿真中机动控制模型研究[J].飞行力学,2007,25(1)∶34-38.
[3]盖玉华,顾文锦,徐怡锋,等.军用飞机运动性能仿真系统设计方法[J].计算机仿真,2009,26(1)∶87-90.
[4]孙明太.航空反潜战术[M].北京∶军事科学出版社,2003∶66-70.
[5]王翠珍,唐金元.现代航空搜潜技术[M].北京∶海潮出版社,2003∶40-42.
[6]郭辉,钱学东,刘启军.直升机吊放声纳搜潜机动建模仿真[J].指挥控制与仿真,2009,31(2)∶87-89.

